Математика/ 3. Теория вероятностей и математическая статистика

к.ф.-м.н. Искакова А.С., Садыбеков Е.Н.

Евразийский национальный университет имени Л.Н. Гумилева, Казахстан

Вероятностное дискретное распределение сумм случайных величин

Предположим, что урна содержит шары, и каждый шар в урне помечен некоторым значением из L₁, … , L_d. Пусть элементы вектора p=(p₁, … , p_d) определяют вероятности извлечения из урны шара, помеченного соответственными значениями L₁, … , L_d, причем

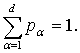
Производится последовательное извлечение n шаров из урны с возвращением, причем неизвестно, какие именно шары были вынуты из урны. Известно только значение u, которое представляет сумму величин L₁, … , L_d на n вынутых из урны шаров. Для изучения данной ситуации требуется построение распределения вероятности u.

Допустим, что V_u представляет число возможных сочетаний r_1vuL₁,…, r_{d vu}L_d, которые в сумме образовали u, где r_1vu,…, r_{d vu} определяют возможное количество вынутых шаров, которые помечены соответствующими значениями L₁, … , L_d. Иначе говоря, из работы [1] следует, что V_u есть число разбиений u на части L₁, … , L_d.

Из результатов работ [2-12] следует следующее утверждение. Вероятность, что случайная величина U примет значение u, есть

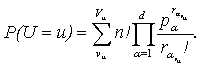(1)

Теорема. Функция, которая определяется в (1), является распределением вероятностей.

Доказательство. Пусть Ω={u} – есть пространство элементарных исходов представленной модели и

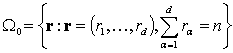
есть пространство элементарных исходов полиномиального распределения, которое имеет следующий вид (8)

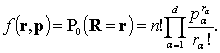
Рассмотрим следующую сумму

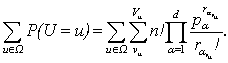
Разумеется, что, если имеет место разбиения u на L₁,…, L_d, то разбиение происходит способами. Для каждого способа v_u = 1, …, V_u разбиения имеем вектор . Также очевидно, что r_vu является решением системы уравнений

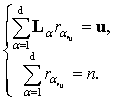(2)

Из чего следует, что вектор

соответствует только одному определенному u. Следовательно, если u ÎW, u₁ÎW и u ¹ u₁, то r_vu ¹ r_vu1 при любых v_u = 1, …, V_u и v_u1= 1, …, V_u1. Таким образом, имеем

Поэтому

и, следовательно, рассматриваемый способ задания вероятностей по формуле (1) является корректным. Теорема доказана.

Очевидно, что на практике не известны элементы вектора p=(p₁, …, p_d). Следовательно формула (1) не находит фактического применения. В связи с этим возникает необходимость определения оценки вероятности (1).

Литература:

1. Andrews G.E. The theory of partitions, Encyclopedia of Mathematics and Its Applications (Rota, et.). G.-C. Addison - Wesley, Reading. 1976. Vol.2. 256p.

2. Искакова А.С. Об одном классе многомерных дискретных распределений, порождаемых урновой схемой с шарами, помеченными прямоугольными матрицами. // Вестник КазГУ, сер. матем., мех., информатика. 2000 г. №1(94). С. 16-20.

3. Искакова А.С. Построение несмещенных оценок вероятностей распределения сумм независимых одинаково распределенных случайных матриц. // Вестник КазГУ, сер. матем., мех., информатика. 2001 г. №4(97). С. 16-20.

4. Искакова А.С. Об одном методе статистического оценивания вероятности оправдываемости прогноза в метеорологии. // Научный журнал Министерства образования и науки Республики Казахстан “Iзденiс” – “Поиск”, сер. естественных наук. 2001 г. № 4, 5. С.182-188.

5. Искакова А.С. Об одном классе многомерных дискретных распределений вероятностей сумм прямоугольных матриц. // Известия МОН РК, НАН РК. 2001 г. № 5. С.85–89.

6. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84.

7. Искакова А.С. Условие существования оценок максимального правдоподобия для параметров одного класса многомерных распределений. // Известия МОН РК, НАН РК. 2004 г. № 1. С.90–95.

8. Искакова А.С. Об определении некоторых оценок одной вероятностной модели// Евразийский математический журнал.- Астана, 2005.- №2. – С. 87-101.

9. Искакова А.С. О факте, что оценки максимального правдоподобия для одного класса дискретных распределений не всегда существуют. Об оценках максимального правдоподобия для параметров одного класса дискретных распределений // Материалы II международной научно- практической конференции “Перспективные новинки науки в технологии”.- Прага-Днепроретровск: Наука и общество-Издательский дом науки и образования, 2005. –Т.13. С.46-48.

10. Искакова А.С. О факте невозможности получения оценок по одному модифицированному методу минимум χ² для параметров распределения сумм случайных элементов// Материалы І международной научно-практической конференции “Наука и технологии-‘2006”.- Белгород: Руснаучкнига, 2006.- Т.12. С. 22-26

11. Искакова А.С. Об одном методе выбора статистической оценки из множества несмещенных // Тезисы докладов международной 11-й межвузовской конференции по математике и механике, посвященной 10-летию ЕНУ им. Л.Н.Гумилева.- Астана, 2006, 25-26 мая. – с . 41.

12. Искакова А.С. О факте невозможности получения оценок, определяемых по методу минимум хи-квадрат и по его модификациям для некоторого распределения// Тезисы международной научной конференции “Современные проблемы дифференциальных уравнений, теории операторов и космических технологий”.- Алматы, 2006, 20-22 сентября. – с . 195-195.