Mathematic/ 4. Applied mathematic
Koblan A., Iskakova A.S.
School -
gymnasium ¹22 of Astana city, Kazakhstan
L.N.Gumilyov Eurasian
National University, Kazakhstan
Estimation
the probability of winning sporting events
We introduce some
concepts and notation. As you know the outcome of any sporting event can be
either win, draw or lose. These outcomes are independent, incompatible and
equally possible. That is, the outcome of one does not affect the outcome of
the other and simultaneously the appearance of two outcomes is impossible
event. They also form a
complete group of events.
If we denote winning as A1, draw as
À0- íè÷üÿ and loss as À-1, then in terms of theory of probabilities Ð(À1) is the probability
of winning, Ð(À0) is the probability
of draw, Ð(À-1) is the probability
of loss. Thus we have the
following system of equations
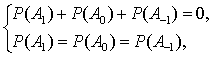
for which the obvious solution is
(1)
Thus, in other words, the probability of the outcome
of any sporting event to its ad satisfy the formula (1).
Let’s even B means that specific
event for specific sporting team on departure is held. Then depend probability P(B|A1) defines probability of sporting
event provided it that the command is winning, the depend probability P(B|A0) is probability of sporting event provided
that the score of the game will be a draw, the depend probability P(B|A-1) defines probability of sporting
event provided it that the command is loss.
As
it’s known that in practice the depend probabilities P(B|A1),P(B|A0)
and P(B|A-1) haven’t the exact values, and therefore need to
build theirs estimates that define their views approximated. For example, such estimates may be the
following:
1. 
is the ratio of the number of won of games on departure for interested team to the total number of
games,
2. 
– the ratio of
the number of games with a score draw on departure for interested team to the total number of games,
3. 
- the ratio of
the number of won of games on departure
for second team to the total number of games.
Then from course the theory of probability and mathematical statistics we
have the follows. The estimation of the probability that will be specific sporting event of team on departure is estimation of full
probability, which is defined as
(2)
Based on Bayes' formula and (2) we can
build a statistical evaluation of the probabilities of outcomes of sports
events of a certain team on departure.
Other words the estimation of probability that the team in a particular
game on departure will win, is defined as
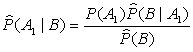
or
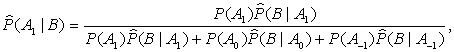
that is
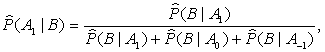(3)
Similarly, the
estimation of the probability that teams in a particular game on departure will draw
is defined as
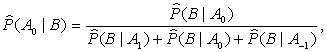(4)
and estimation of
probability that teams in a particular
game on departure lose is defined as
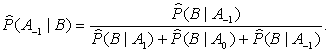(5)
We
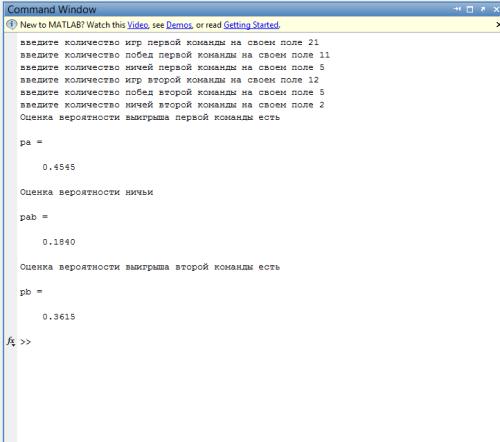
have developed the following program in the Matlab.
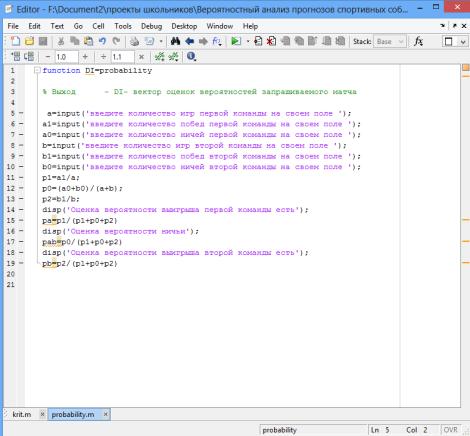
Pic.1. The program is a
system Matlab to calculate estimates of the probabilities (3)-(5).
Example. Consider the match
Newcastle vs. Leicester of championship of the European football in the Premier
League. We define the estimation of probability of win of the first team, draws and the win of the second team.
To do this, using the statistical information (in this example - for the
preceding season, it is desirable - the highest number of seasons), we find 
,
,
:
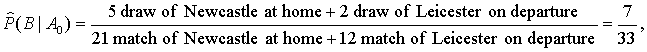
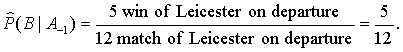
Pic. 2. Implementation
of the program in a system Matlab to calculate estimates of the probabilities (3)-(5).
Accordingly,
the estimation of the probability of winning of the first team is defined as
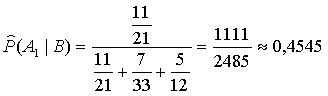
or
approximately 45.45%. Similarly, we obtain the estimation of probability of a
draw
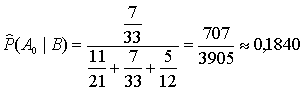
or approximately 18,4%.
Also estimation of the probability of winning for the second team is defined as
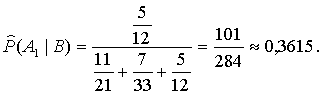
or approximately 36,15%.
Similar calculations through the program in a system Matlab have the
form shown in Figure 2.
References:
1.
Hájek, A., 2009, “Fifteen Arguments
Against Hypothetical Frequentism”, Erkenntnis,
70, 211–235. Also in Eagle 2010.
2.
Kallenberg, O. (2005) Probabilistic Symmetries and Invariance
Principles. Springer
-Verlag, New York. 510 pp. ISBN
0-387-25115-4.
3.
Lee, Peter M. (2012). "Chapter 1". Bayesian Statistics. Wiley. ISBN 978-1-1183-3257-3.
4.
Phillips, L. D.;
Edwards, Ward (October 2008). "Chapter 6: Conservatism in a Simple
Probability Inference Task (Journal of Experimental Psychology (1966) 72:
346-354)". In Jie W. Weiss and David J. Weiss. A Science of Decision
Making:The Legacy of Ward Edwards. Oxford University Press.
p. 536. ISBN 978-0-19-532298-9.
5.
Ayman I.
Construction of the most suitable unbiased estimate distortions of radiation
processes from remote sensing data //Journal of Physics: Conference Series. –
IOP Publishing, 2014. – Ò. 490. – ¹. 1. – Ñ.
012113.