В.В.Подгорная

Минск, Учреждение образования Федерации профсоюзов Беларуси «Международный университет «МИТСО»

Система задач высшей математики, направленных на выявление образовательного уровня студентов экономических специальностей

В процессе изучения высшей математики практические упражнения и задачи призваны выполнять разнообразные функции. Задачи можно считать самым эффективным средством для изучения и усвоения математических понятий и математической теории. Велика их роль и в развитии у обучаемых практических умений и навыков. Рассмотрим наиболее важные аспекты обучения студентов экономических специальностей решению задач по высшей математике, для чего прежде всего обозначим основные цели при обучении решению задач.

Образовательная цель состоит в том, что при решении задач студент приобретает математические знания и развивает умение решать задачи определенного типа, а при достаточной тренировке у него вырабатывается навык решения задач, что в целом повышает математическое образование. Кроме этого обучение решению задач развивает мышление, а непосредственно решение математических задач приучает выделять посылки и заключения, данные и исходные, находить общее, сопоставлять и противопоставлять факты, проводить анализ и синтез фактов, что необходимо в профессиональной деятельности любого специалиста.

Рассмотрим воспитательную цель математических задач. Прежде всего задача воспитывает своим содержанием, текстовым смыслом, поэтому для студентов, получающих экономическое образование, важны задачи с соответствующим содержанием. Правильно поставленное обучение решению математических задач воспитывает у студентов настойчивость в преодолении трудностей, уважение к труду.

Остановимся на практической цели математических задач, при решении которых студент обучается применению математических знаний к практическим наукам, готовится к практической деятельности и решению задач, которые она выдвигает.

Особую роль в обучении высшей математики играют задачи повышенной трудности, которые приносят больше пользы, чем решение системы стереотипных задач и позволяют обучаемым рассматривать различные варианты решений, выбирая наиболее рациональные из них. Решение задач повышенной трудности позволяет студенту применять весь арсенал знаний по высшей математике и другим наукам. Надо отметить, что рациональные приемы решения задач не появляются сами, им необходимо обучать.

Рассмотрим систему задач по высшей математике, через решение которых реализуются основные образовательные задачи и цели профессионального образования.

Задачи целесообразно систематизировать следующим образом:

1) первая группа задач, через решение которых студенты изучают основные математически понятия и получают математическое образование;

2) вторая группа задач, для решения которых необходимо применять как знания математики, так и знание экономических дисциплин. Это группа задач, которые иллюстрируют связь математики и экономики;

3) третья группа задач повышенной трудности, решение которых развивает у студентов творческое мышление.

Продемонстрируем систему задач через изучение конкретных тем учебной программы по высшей математике.

Тема: Числовые последовательности. Предел числовой последовательности

I группа задач.

1. Найти пределы последовательностей:

1.1. ; 1.2 ; 1.3

II группа задач.

2.1. Прирост населения страны составляет процентов в год. За сколько лет население удвоится? Дать ответ при и

2.2. Коммерческий банк аккумулирует средства предприятий в среднем на шесть месяцев. За это время он успеет три раза «прокрутить» эти деньги в виде краткосрочных кредитов, выдаваемых частным предпринимателям на три месяца под 4% в месяц. Сколько процентов прибыли получает банк в результате этой операции?

2.3. В соответствии с условиями предыдущей задачи необходимо рассчитать, что выгоднее банку: кредитовать из собственных средств предприятия на условиях 20% годовых или заниматься указанной деятельностью?

III группа задач.

3.1. Найти все тройки положительных чисел a,b,c такие, что существует конечный предел и найти предел.

3.2. Пусть – последовательность многочленов, степень которых не превосходит фиксированного числа m. Доказать, что если 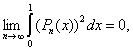то для любого k,

3.3. Вычислить предел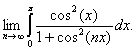

Тема: Интегралы. Неопределенный и определенный интеграл

1.1. Вычислить интегралы:

a) ;b) ; c) ; d)

1.2. Вычислить площади фигур:

a) ; b) ; c);d)

1.3. Вычислить несобственные интегралы в случае их сходимости:

a) ; b) ; c) ;d)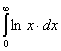

II группа задач.

2.1. Найти стоимость перевозки M тонн груза по железной дороге на расстояние l км при условии, что тариф за перевозку одной тонны убывает на a руб. на каждом последующем километре.

2.2. Мощность потребляемой городом электроэнергии выражается формулой 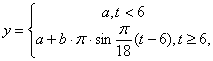где t – текущее время суток. Найти суточное потребление электроэнергии при a=15000 кВт, b=12000 кВт.

III группа задач.

3.1. Доказать равенство: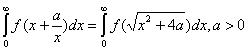

3.2. Найти длину дуги линии от начала координат до ближайшей точки с вертикальной касательной.

3.3. Что больше: или .

Тема: Матрицы. Системы линейных уравнений

I группа задач.

1.1. Найти матрицы , где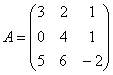

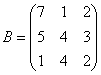
1.2. Решить систему линейных уравнений методом Гаусса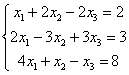

1.3. Показать, что векторы образуют базис.

II группа задач.

2.1.Отрасль состоит из четырех предприятий. Векторы выпуска продукции и матрица коэффициентов прямых затрат имеют вид:

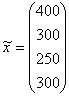
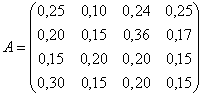
Найти вектор объемов конечного продукта, предназначенного для реализации вне отрасли.

2.2. Предприятие выпускает три вида продукции с использованием трех видов сырья, характеристики производства указаны в таблице 1.

Таблица 1 Характеристики производства

Вид сырья	Расход сырья по видам продукции, вес ед./изд.			Запас сырья вес.ед.
	1	2	3
1	5	12	7	2350
2	10	6	8	2060
3	9	11	4	2270

Найти объем выпуска каждого вида при запасах сырья.

III группа задач.

3.1. Пусть a,b>0, . Найти такую матрицу B, что

3.2. Решить матричное уравнение: где – нулевая матрица.

3.3. Пусть A – квадратная матрица с (невырожденная), в каждой строке которой стоит только одно число, отличное от 0 и равное Доказать, что при некотором натуральном m справедливо равенство где – транспонированная матрица A.

Использованные источники

1.М.С. Красс, В.П. Чупрынов. Математика для экономистов. М.; СПб, 2010.

2.И.Ю. Попов. Задачи повышенной трудности в курсе вышей математики: учеб. пособие. СПб, 2008.

3.М.С. Красс. Математика для экономических специальностей. М.: Дело, 2003.