Уалиев Заир Гахипович, д.т.н., профессор.

Оган Нурбек. Магистрант 2 курса.

Казахский Национальный Педагогический Университет им. Абая,

Г.Алматы

АЛГОРИТМ КИНЕМАТИЧЕСКОГО АНАЛИЗА ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ С НЕЛИНЕЙНОЙ ФУНКЦИЕЙ ПОЛОЖЕНИЯ

Основными передаточными механизмами машинных агрегатов являются рычажные, кулачково-рычажные с плоскими, пазовыми или пространственными кулачками. По расчету и исследованию кулачковых механизмов различных машин выполнено большое количество работ и имеется обширная литература, в которой приводятся алгоритмы их кинематического и динамического расчета, в том числе с использованием ЭВМ. В дальнейшем при построении динамических моделей механизмов переменной структуры всегда даются ссылки на функции положения и передаточные отношения. В связи с этим в этом разделе приводятся выражения функции положения типовых передаточных механизмов и алгоритмы кинематического анализа.

Заданным параметром для кинематического анализа кулачково-рычажных механизмов является значение радиуса-вектора профиля кулачка , зависящего от полярного угла /1/. При этом необходимо получить аналитические выражения для функции положения - угол поворота кулачка. Для определения передаточных функций первого и второго порядка достаточно функцию положения последовательно дифференцировать по углу поворота кулачка. Во избежание громоздких выкладок и неудобных расчетных зависимостей определение функций положения, скорости и ускорения ведомого звена кулачково-коромыслового механизма производится методом обращенного движения.

Ниже будут рассмотрены вопросы алгоритмизации кинематики типовых схем: плоских и пространственных кулачково-коромысловых механизмов и четырехзвенника.

Задачу определения функций положения и передаточных функций кулачково-коромыслового механизма при заданных длин звеньев и радиуса профиля кулачка . Рассмотрим два положения коромысла (рис.1) в обращенном движении, соответствующих начальному положению и текущему положению.

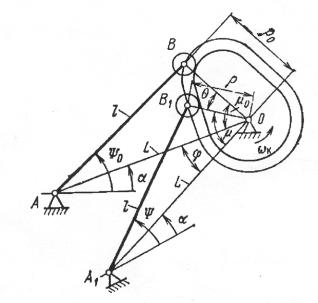
Рисунок 1. Схема плоского кулачково-коромыслового механизма

Для функции положения плоского кулачково-коромыслового механизма имеем следующие соотношения:

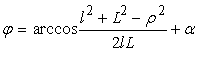(1)

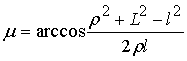. (2)

Зависимость между углом поворота кулачка и полярным углом можно записать в виде

,

где - угол, соответствующий начальному положению, вычисляется по формуле (2).

При заданных угловой скорости и ускорении кулачка, угловая скорость и ускорение коромысла определяются из следующих выражений:

;

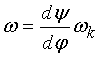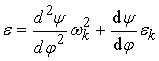. (3)

Аналоги угловой скорости коромысла определяются дифференцированием выражения (1) по углу :

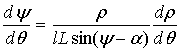. (4)

Аналогично из выражения (2) найдем:

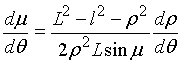. (5)

Из выражения (3) следует:

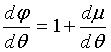(6)

Обозначив

;

и разделив соотношение (4) на (6) с учетом (5), получим следующее выражение для аналога угловой скорости коромысла:

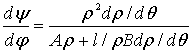(7)

Продифференцировав (7) по , разделив на (6), определим аналог ускорения коромысла:

,

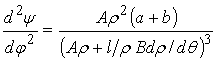где

;

.

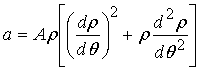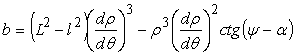Рассмотрим задачи кинематического анализа пространственного кулачково-рычажного механизма. Развернем цилиндрический кулачок по среднему радиусу r контакта ролика и паза, а затем дадим развертке и коромыслу AB обращенное движение со скоростью , противоположной окружности скорости цилиндрического кулачка. Из рис. 2, учитывая, что угол отчитывается от вертикали, имеем

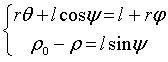; (8)

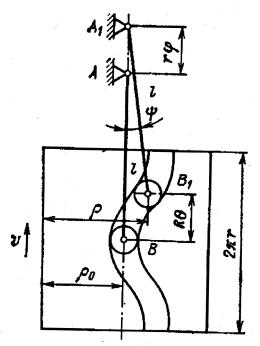
Рисунок 2. Схема пространственного кулачкового механизма

Отсюда можно получить функцию положения в параметрическом виде:

;

.

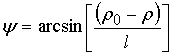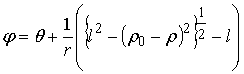Тогда

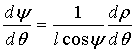; (8)

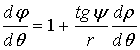. (9)

Разделив выражение (8) на (9), для аналога скорости коромысла AB имеем

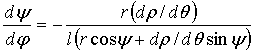(10)

Аналог ускорения коромысла AB определим, дифференцируя (10) по и разделив на выражение (9), после чего имеем

.

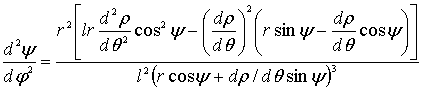Кинематическое исследование плоского четырехзвенника (рис. 3) будем вести методом замкнутых векторных контуров.

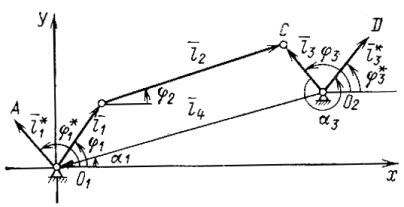
Рисунок 3. Схема четырехзвенника

Векторное уравнение замкнутости контура будет

,

или в проекциях на оси координат

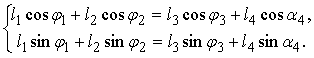(11)

Обозначив

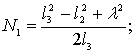
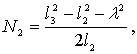
получим систему уравнений

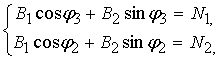
из которой определим

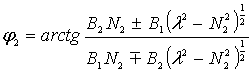
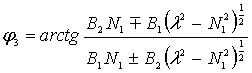
Очевидно, что после дифференцирования (12) по и некоторых преобразований получим для аналогов скоростей следующие выражения:

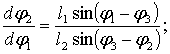
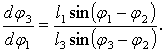
Дифференцируя последние выражения аналогов скоростей по, получим выражения для аналогов ускорений:

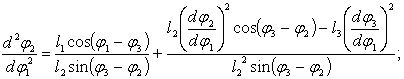
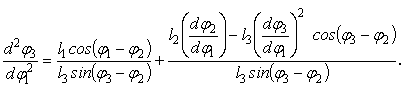
Рассмотрим передачу движения от звеньев четырехзвенника к ползуну. Исследуем движение ползуна (рис. 4) методом замкнутых контуров:

.

или в проекциях на оси координат

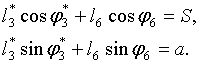
Отсюда получим выражение для положения

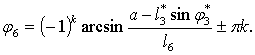
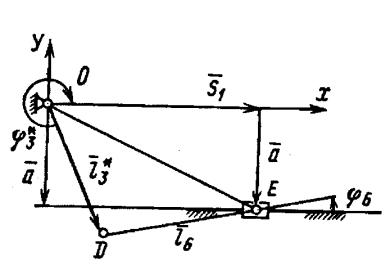
Рисунок 3. Схема кривошипно-ползунного механизма

Тогда положение ползуна определяется из соотношения

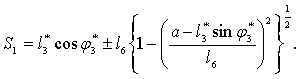
Дифференцируя уравнения в проекциях по , получим выражения для аналогов скорости и ускорения

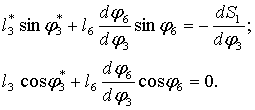
Из этой системы получим выражения для аналогов угловой и линейной скорости ползуна в виде

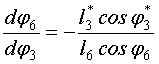и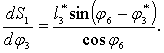

Повторным дифференцированием выше приведенной системы уравнений и некоторым их преобразованием получим аналог линейного ускорения ползуна

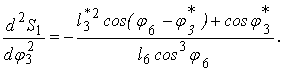
Выше приведенные выражения и последовательности решения уравнении связи для блочных систем или групп шарнирных и кулачково-рычажных механизмов определяют алгоритм вычисления плоских механизмов 2 класса с нелинейными функциями положения.