Математика/4. Прикладная математика

К. ф.‑м. н. Карнаух Т.О., Хопта О.А.
Київський національний університет імені Тараса Шевченка

Побудова завдань для адекватного оцінювання знань

На сьогодні актуальною є проблема адекватного оцінювання знань. Різноманітні контрольні, іспити, тести мають на меті виявити, що знає і чого не знає той, кого оцінюють, і визначити його місце в загальному рейтингу певної групи людей, які також проходили оцінювання, або ж віднесення його до однієї з категорій успішності.

Метою даної роботи є вирішення проблеми об’єктивності оцінювання в плані того, щоб ті, хто знають найкраще, отримали відмінну оцінку, ті, хто трохи гірше – добру оцінку, тощо. Одним з шляхів вирішення питання «об’єктивності» є спроба будувати завдання, виходячи із заданої середньої оцінки отриманої за контрольну.

Уточнимо постановку задачі. Нехай маємо k задач, з яких має складатися контрольна і кожна з яких розв’язувалася різними особами в минулі періоди часу. За кожного розв’язання за задачу ставилася певна кількість балів, причому необов’язково максимально можлива. Під спостереженням будемо розуміти частину від 1, на яку була розв’язана задача. Під розв’язуваністю i‑ої задачі будемо розуміти середнє арифметичне спостережень над цією задачею і позначатимемо його . Отже, вхідними даними є розв’язуваності заданих k задач. При формуванні оцінки за виконане завдання кожна задача враховується з певною додатною цілою вагою. Вагу i‑ої задачі позначимо . Тоді побудова завдання зведеться до задачі визначення ваг його задач (вагових коефіцієнтів). Приймемо, що абсолютно правильне виконання кожної задачі завдання повинно давати оцінку 100 балів. У найпростішому випадку слід вимагати, щоб існувала можливість отримати максимальний бал, тобто сума вагових коефіцієнтів має дорівнювати 100, тобто  = 100.

Але при цьому можлива ситуація, коли найскладніші задачі мають настільки велику вагу, що результати виконання завдання будуть переважно незадовільними і не відображатимуть реальний рівень знань. Тоді введемо додаткову вимогу до вагових коефіцієнтів: середній бал, отриманий за завдання групою студентів, має приблизно дорівнювати певній величині S (SÎN), скажімо, S = 75. Отже, S.

Зрозуміло, що вага задачі не може бути ні близькою до нуля, ні близькою до 100, тому логічним є обмеження ваг зверху і знизу: .

У підсумку маємо таку систему вимог для визначення вагових коефіцієнтів.

= S,

 = 100,

,

(), a, b, S – цілі додатні числа.

Необхідною умовою для того, щоб задача мала розв’язок, є виконання обмежень на a і b, а саме a £ 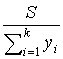£ b.

Хоча ця задача й є задачею цілочисельного лінійного програмування, але покажемо, як можна звести її до звичайної задачі лінійного програмування.

Нехай w = 100/k і . Тоді систему вимог, опустивши умову цілочисельності, можна записати так

 = ,

= 0,

, де w = 100/k .

Маємо задачу знаходження опорних розв’язків системи з двома рівняннями та k невідомими d_i (iÎ). Її можна розв’язати симплекс-методом або використати поліноміальний алгоритм.

Отримані дійсні значення d_i будуть задавати дійсний вагові коефіцієнти w_i = . Округлимо отримані дійсні значення до найближчих цілих. Нехай r(x) є округленням числа x до найближчого цілого, тобто

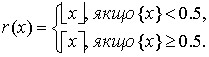
Спочатку покладемо c_i = r(w_i), m = . Зазначимо, що m < k/2. Далі змінимо m з k значень c_i на 1 так, щоб сума вагових коефіцієнтів дорівнювала 100. Отримані значення c_i будуть шуканими вагами задач.

Оцінимо, наскільки сума відхиляється від S. Під час округлення ця сума могла відхилитися від S не більше, ніж на . Під час зміни деяких з значень c_i на 1 могла бути внесена ще додаткова похибка не більша за m. Отже, загалом £ m + £ m + k/2 < k. На практиці похибка, як правило, виявляється меншою за k.

Хоча й наведений метод не дає точного розв’язку, але слід зазначити, що точний розв’язок у цілих числах не завжди можливий, оскільки розв’язуваності, що є коефіцієнтами, є дійсними числами. Крім того, цей метод гарантовано дає доволі непогане наближення розв’язку, що є його беззаперечною перевагою. Також він може бути реалізований за поліноміальний час.

Література:

1. Хемди А. Таха Глава 3. Введение в исследование операций — 7-е изд. — М.: «Вильямс», 2007. — с. 95-141.

2. Акулич И.Л.  Математическое программирование в примерах и задачах/ И. Л. Акулич. —М.: Высшая школа, 1986. — 319 с.