Уалиев Заир Гахипович, д.т.н., профессор.

Оган Нурбек. Магистрант 2 курса.

Казахский Национальный Педагогический Университет им. Абая,

г.Алматы

МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ С ГОЛОНОМНЫМИ СВЯЗЯМИ

Для голономных систем число степеней свободы определяется числом независимых координат, описывающих положение каждой точки системы. Эти координаты называются обобщенными и обозначаются q₁, q₂, q_s где s-число степеней свободы. Число обобщенных координат одновременно является минимальным числом координат, которыми можно определить возможные положения голономной системы. Наряду с обобщенными координатами при исследовании динамики механизмов, целесообразно пользоваться некоторыми вспомогательными координатами, связанными с обобщенными координатами и уравнениями связи. Эти координаты называются избыточными или лишними, число которых должно совпадать с числом дополнительных уравнений связи.

Кинетическая энергия голономной системы s степенями свободы равна

.

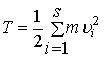В общем случае радиус-векторы точек зависят от обобщенных координат, а при нестационарных связях еще и от времени, тогда для скорости точки можно записать следующие выражения

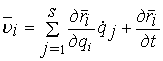
Подставляя из этого уравнения в выражение кинетической энергии, получим

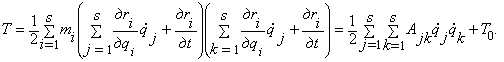(2.21)

Здесь приняты следующие обозначения

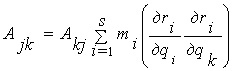
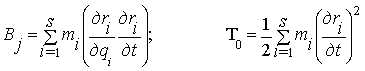
Для динамических моделей механизмов со стационарными связями последние выражения тождественно равны нулю, т.е. и кинетическая энергия описывается однородной квадратичной функцией (квадратичной формой) обобщенных скоростей с коэффициентами , являющимися в общем случае некоторыми функциями обобщенных координат.

В случае , имеем

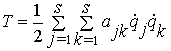
называют инерционными коэффициентами.

Если считать, что все обобщенные координаты являются малыми, предполагая, что - дифференцируемые функции и разлагая каждый из коэффициентов в ряд Маклорена, получаем

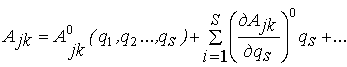
Индексом «0» обозначены значения функции в положении равновесия, при

Кинетическая энергия при будет записана в форме (2.21) с точностью до второго порядка малости. При этом точность уравнений движения будет соответствовать первому порядку малости. Например, кинетическая энергия для системы с тремя степенями свободы имеет следующий вид:

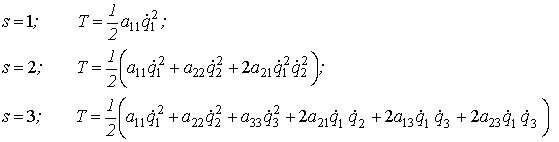(2.22)

Согласно принципу виртуальных перемещений сумма элементарных работ внешних сил может быть представлена в виде:

(2.23)

В этом случае обобщенная сила складывается из потенциальной и потенциальной составляющих. При этом , где П -потенциальная энергия. При определении непотенциальной составляющей следует для каждого конкретного случая записать выражение элементарных работ (2.23) и приравнивать коэффициенты при одинаковых вариациях обобщенных координат . Непотенциальные силы могут зависеть от времени, обобщенных скоростей, обобщенных координат.

В общем случае потенциальная энергия системы является функцией обобщенных координат и времени. В механизмах потенциальная энергия формируется в основном за счет упругих деформаций. В тяжелых машинах и в открытых кинематических цепях приходится также принимать во внимание и потенциальную энергию сил тяжести.

Предполагая, что функция V, характеризующая потенциальную энергию, в окрестности положения равновесия непрерывна и дифференцируема, разложим ее в ряд Маклорена

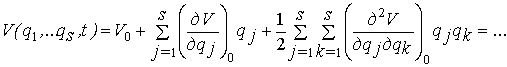
Здесь, как и раньше, индекс «0» соответствует .

В положении статического равновесия потенциальная составляющая обобщенных сил равна нулю, а следовательно, .

Таким образом, с той же точностью, как и при записи кинетической энергии, потенциальная энергия в окрестности положения равновесия может быть выражена:

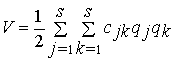, (2.24)

где - коэффициенты жесткости.

Квадратичная форма (2.24), так же как и выражение (2.22), является знакопостоянной и притом положительной. Это вытекает из условия устойчивости положения равновесия, сформулированного в теореме Лагранжа-Дирихле: если для материальной системы, находящееся в консервативном силовом поле и подчиненной голономным, идеальным и стационарным связям, потенциальная энергия имеет в положении равновесия минимум, то это положение равновесия является устойчивым.

В данном случае, поскольку, с одной стороны, V₀=0, а с другой, - это значение, согласно теореме Лагранжа-Дирихле, одновременно отвечает минимуму, при любом отклонении от этого положения имеем V>0. Тогда из предыдущих выражений для коэффициента жесткости имеем:

.

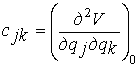Во многих случаях удобнее находить квазиупругие коэффициенты квадратичной формы из выражения потенциальной энергии, соответствующего конкретной системе.

Для системы с одной степенью свободы существование минимума потенциальной энергии в положении равновесия определяется условием 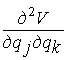>0, а для системы с конечным числом степеней свободы эти условия обеспечивают соотношения между параметрами системы, при которых всякому перемещению обобщенных координат соответствует положительно приращение потенциальной энергии.

Для определения условий, при которых рассматриваемая квадратичная форма (2.24) будет определенно положительной, воспользуемся критерием Сильвестра о знакоопределенности квадратичной формы. Эти критерии формулируется следующим образом:

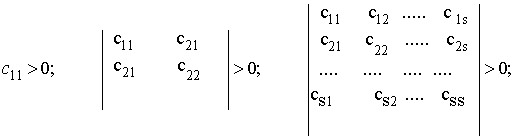(2.25)

Для потенциальной энергии системы будут:

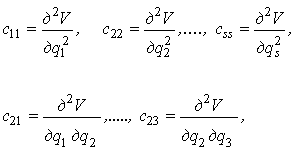
и т.д.

При этом с₁₂=с₂₁.

Теорема Лагранжа-Дирихле не дает оснований для суждения о том, каково будет равновесие системы, если ее потенциальная энергия в равновесном положении не имеет минимума. В этом случае необходимо пользоваться теоремами А.М.Ляпунова, а для неконсервативной системы обычно пользуются теорией малых колебаний.

Для получения дифференциальных уравнений движения системы применяем уравнения Лагранжа второго рода, который имеет вид

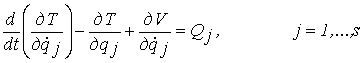
Производные 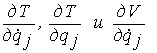должны быть вычислены с точностью до величины первого порядка малости, при дифференцировании по порядок малости понижается, поэтому величины кинетической и потенциальной энергии следует вычислять с точностью до малых величин второго порядка. Пренебрежение малыми величинами высших порядков малости вносит некоторую погрешность в полученные результаты, но эта погрешность при практических расчетах окупается значительным упрощением рассмотрения нелинейных систем, т.е. рассмотрением системы, приближенно описывающие линейными дифференциальными уравнениями

В случае, когда кинетическая и потенциальная энергии могут быть представлены в виде квадратичных форм с постоянными коэффициентами, получаем систему s дифференциальных уравнений второго порядка:

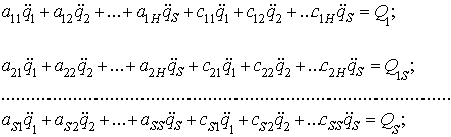(2.26)

Использование инерционных и квазиупругих коэффициентов приводит к автоматизму при построении математической модели механических систем. При составлении системы дифференциальных уравнений для механизмов часто встречается случай, когда какая-либо координата не входит в выражение потенциальной энергии. Тогда при имеем:

(2.27)

Здесь L=T-М – функция Лагранжа.

Координаты , удовлетворяющие условию (2.27), называют циклическими.

При рассмотрении динамики механизмов с нелинейной функцией положения оказывается, что коэффициенты в выражении для кинетической энергии не могут быть приняты постоянными, так как не все обобщенные координаты являются малыми величинами. Например, текущий угол поворота ведущего звена механизма является конечной величиной. В случае, когда обобщенная координата не входит в выражение для потенциальной энергии, но от нее зависят в явном виде кинетическая энергия, то . Такую координату называют квазициклической. В случае при подстановке функции Т в уравнение Лагранжа второго рода приходится осуществлять дифференцирование сложных выражений и производить громоздкие преобразования. Существенное упрощение может быть достигнуто, если устранить необходимость выражения всех координат системы через обобщенные координаты введением избыточных координат.

Особая форма уравнений Лагранжа второго рода с избыточными координатами. Пусть, кроме s обобщенных координат q₁,…,q_s, вводятся в рассмотрение n избыточных координат q_s+1,…,q_s+n. Тогда уравнения Лагранжа с избыточными координатами примут вид.

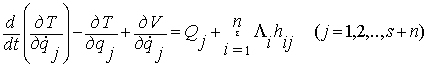(2.28)

Здесь - некоторые функции, которые будут выявлены ниже, причем носит название множителя Лагранжа.

Физический смысл членов с множителями Лагранжа связан с появлением дополнительных реакций идеальных связей, которые в данном случае полностью не исключаются из уравнений Лагранжа из-за превышения числа координат над числом степеней свободы .

Избыточные координаты не являются независимыми, поэтому в дополнение к (2.28) должны быть составлены уравнений связи, которые в общем виде записываются следующим образом:

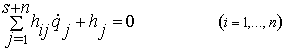(2.29)

В форме (2.28) и (2.29) уравнения движения могут применяться и для неголономных систем, например для приводов с вариатором скорости.

Уравнения голономных связей имеют вид

Продифференцируя это выражение по времени, имеем:

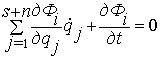(2.30)

Сопоставляя уравнения (2.29) и (2.30), находим

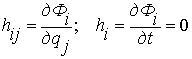(2.31)

Учитывая эти выражения из уравнении (2.28), получаем уравнения Лагранжа второго рода избыточных координатах в виде

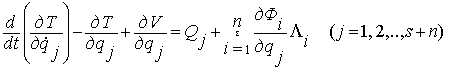
Избыточные Координаты Выберем Таким Образом, Чтобы По Всем Координатам . Тогда Независимо От Степени Малости Имеем . При Линейных Упругих Характеристиках Звеньев Выражения Для Кинетической И Потенциальной Энергии Относительно Всех Координат, Включая Избыточные, Опять Имеют Вид Квадратичных Форм (2.23) И (2.24), И Соответствующая Система Дифференциальных Уравнений Может Быть Записана Аналогично Системе (2.24)

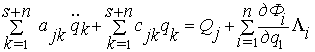(j =1,…,s+n) (2.32)

c той разницей, что таких уравнений будет s+n и в правой части уравнений появятся дополнительные члены с множителями Лагранжа.

Уравнения Аппеля, так же как и уравнения Лагранжа с избыточными координатами, пригодны для описания неголономных систем. Однако здесь мы ограничимся записью этих уравнений для голономных систем:

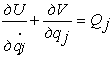, (j=1,…s)

Здесь U – энергия ускорений, которая описывается выражением, аналогичным кинетической энергии, если вместо скоростей подставить ускорения. При этом, составляя выражение для U, достаточно учесть члены, которые зависят от обобщенных ускорений , так как остальные члены не войдут в это уравнение.

Хотя для голономных систем уравнения Аппеля являются по существу лишь иной записью уравнений Лагранжа второго рода, использование этой формы в ряде случаев дает ощутимые преимущества [81].