Технические науки/Электротехника и радиоэлектроника

Профессор Алиев И.И.

Северокавказская государственная гуманитарно-технологическая академия

Об основных уравнениях и схемах замещения

электрических машин в режиме холостого хода

Предметом анализа являются основные уравнения, схемы замещения и векторные диаграммы электрических машин и трансформаторов в режиме холостого хода. Поскольку они представлены во всех вузовских учебниках по электрическим машинам, например, в [1] и знакомы читателю, в дальнейшем ссылки на литературу не приводятся. Причиной анализа общеизвестных уравнений, схем замещения и векторных диаграмм является несоответствие их, по мнению автора, реальным процессам, происходящим в машинах. Начнем с анализа основных уравнений и схем замещения однофазного двухобмоточного трансформатора в режиме холостого хода.

В этом режиме трансформатор представляют как катушку с сердечником, поскольку события, происходящие во вторичной обмотке (т.е. наведение в ней ЭДС от основного магнитного потока), не влияют на электромагнитные процессы в трансформаторe в целом. Первичное напряжение uопределяет величину тока i, который создает основной магнитный поток Ф и поток рассеяния Ф. ЭДС в обмотках от основного потока в первичной и вторичной обмотках:

е = - w(dФ / dt); е = - w(dФ / dt). (1)

Поток рассеяния наводит в первичной обмотке ЭДС самоиндукции:

е = - w(dФ/ dt).

ЭДС самоиндукции может быть определена и по закону Ленца:

е = - L(di/dt),

где L- индуктивность рассеяния первичной обмотки. Величину е называют также падением напряжения на её индуктивном сопротивлении рассеяния. Таким образом, напряжение u на первичной обмотке уравновешивается ЭДС взаимной индукции е, ЭДС самоиндукции е и падением напряжения на активном сопротивлении R обмотки w:

u= w(dФ / dt)+ L(di/dt) + Ri, или: u= е+ е + Ri. (2)

Далее авторы полагают, что поскольку по модулю е» е и е» Ri, то ими можно пренебречь, и выражение (2) вырождается в простейшее: u= е.

Переходя к векторной форме величин, записывают:

U= -E. (3)

Однако упрощение на этом не кончается. Ток холостого хода принимают равным его реактивной составляющей: I= I, полагая что его активной составляющей можно пренебречь: I= 0. Это означает, что активное сопротивление намагничивающего контура равно нулю. Для этих условий записывают:

Ė= - jXİ, (4)

где X- главное индуктивное сопротивление (сопротивление взаимоиндукции).

Далее авторы приводят схему замещения а) и векторную диаграмму б) идеализированного трансформатора в режиме холостого хода (рис.1).

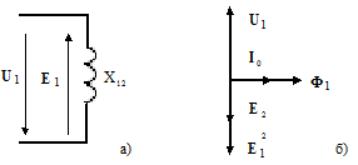
Рис.1. Традиционные схема замещения а) и векторная диаграмма б)

идеализированного трансформатора в режиме холостого хода

Здесь мы сталкиваемся с первым противоречием. Оно заключается в том, что если величины напряжения U и ЭДС E равны и противоположны по знаку, то ток такого идеализированного трансформатора (намагничивающий ток) равен нулю, и никакие физические процессы в таком трансформаторе невозможны в принципе. Следовательно, в традиционном представлении понятия идеализированный трансформатор или идеализированная асинхронная машина физического смысла, вероятно, не имеют. Соответственно невозможны и не имеют никакого смысла схема замещения и векторная диаграмма (рис.1), приводимые авторами в учебниках по электрическим машинам.

Это очевидное противоречие можно преодолеть, предположив, что либо: 1) ЭДС взаимной индукции E в трансформаторе всегда меньше противоположно направленного первичного напряжения U, либо: 2) угол между этими равными векторами меньше величины π. Первый вариант возможен лишь при условии, что учитываются активные потери в трансформаторе, второй - если учесть ЭДС самоиндукции трансформатора в режиме холостого хода. Однако и в том и в другом случае равенство (3), используемое в теории электрических машин для описания режима холостого хода, неверно по существу.

Поскольку, как видим, учет потерь в электрических машинах необходим в принципе, рассмотрим природу потерь в трансформаторе в режиме холостого хода. В сущности, можно лишь условно говорить о режиме холостого хода. Дело заключается в том, что всякий двухобмоточный трансформатор в этом режиме (как, впрочем, и в режиме нагрузки) имеет как бы третью обмотку, которая представляет собой интегральный короткозамкнутый контур его магнитопровода. В нем циркулируют токи Фуко, что и обуславливает известные потери в стали, а её перемагничивание - потери на гистерезис. Другим видом потерь являются потери в меди трансформатора, которые действительно невелики в режиме холостого хода. Потери в меди и потери в стали от вихревых токов относят к активным потерям в виде энергии тепла.

Потери на гистерезис связаны с формированием в магнитопроводе переменного рабочего магнитного поля. Другими словами, это – энергия, связанная с непрерывным перестроением доменов вдоль вектора магнитной индукции поля первичной обмотки. Происходит ли при этом преобразование электромагнитной энергии в энергию тепла не вполне ясно, хотя явление это учитывается именно как потери на гистерезис. Катушка с сердечником является концентратором электромагнитной энергии в виде энергии магнитного поля. Как известно взаимный обмен реактивной мощностью между источником и реактивным элементом (идеальной катушкой или конденсатором) происходит в течение одного периода дважды, при этом обмен осуществляется без потерь.

Таким образом, «реактивное» сопротивление по своей природе в принципе отличается от активного сопротивления. Индуктивное сопротивление есть проявление в идеальной катушке электромагнитной инерции при запасании или возврате ею электромагнитной энергии, а «падение напряжения» на реактивном сопротивлении на самом деле является ЭДС самоиндукции, другими словами, «реактивное сопротивление» - это не пассивный элемент цепи, как резистор, а является источником энергии. Поэтому используемые обычно в электротехнике понятия индуктивное или емкостное сопротивления являются, полагаем, весьма условными и не вполне адекватны своему названию.

Далее, ЭДС самоиндукции в режиме холостого хода: Ė = - jXI.

Сравним это выражение с (4). Для асинхронных машин и трансформаторов X составляет 3-30 % от X. Иначе говоря, E= (0,03 - 0,3)E . Разница в (3 - 30%) между напряжением и ЭДС и обеспечивает ток холостого хода и намагничивающий ток машин. Следовательно, и в идеализированном трансформаторе напряжение первичной обмотки компенсируется суммой ЭДС взаимоиндукции, ЭДС самоиндукции и падением напряжения RI, которое учитывает суммарные потери в стали в интегральном контуре магнитопровода:

U= E+ E+ RI = E+ jXI+ RI (5).

Этому уравнению соответствует уточненная векторная диаграмма, представленная на рис.2,а.

Теперь перейдем к случаю реального трансформатора. Ток холостого хода складывается из активной и реактивной составляющих: I=.

Намагничивающий контур в этом случае представляется в виде параллельно, а чаще - последовательно соединенных активного R и индуктивного X сопротивлений этого контура. Принимается обычно, что главное сопротивление взаимоиндукции X = X. Соответственно полное сопротивление намагничивающего контура равно Z.

Авторы для этого случая записывают:

U= - E= ZI = RI+ jX I. (6)

Соответствующая векторная диаграмма, традиционно приводимая в литературе, представлена на рис. 2, б.

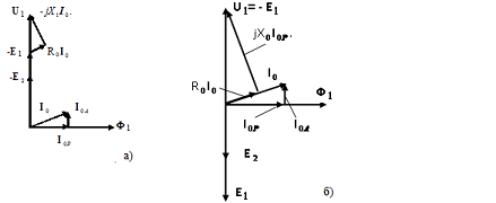
Рис.2. Уточненная а) и традиционная б) векторные диаграммы трансформатора

в режиме холостого хода

Однако выражение (6) влечет за собой теперь уже три ошибки.

Во-первых, как уже указывалось выше, при таком равенстве ток в первичной обмотке трансформатора невозможен в принципе.

Действительно: I= (U- E) Z = (0) Z=0.

Во-вторых, как отмечалось, ЭДС взаимной индукции для всех случаев и режимов равна: E= - j XI, либо E= - j XI.

Из изложенного следует, что общепринятая векторная диаграмма, приведенная на рис. 2,б, не соответствует реальности.

В-третьих, такая запись физически означает, что и активные, и "реактивные" падения напряжения намагничивающего контура и соответствующие потери компенсируются не за счет источника первичного напряжения, а за счет ЭДС E, поскольку эти падения напряжения в выражении (6) как бы "вмонтированы" в "структуру" ЭДС. Однако активная составляющая падения напряжения на сопротивлении R не имеет к ЭДС Eникакого отношения, поскольку обусловлена протеканием тока I, который первичен не только по отношению к E, но и по отношению к потоку Ф, вызывающему к жизни ЭДС E.

Что касается "падения напряжения на индуктивном сопротивлении X", то это и есть ЭДС взаимной индукции E. Таким образом, падение напряжения на активном сопротивлении намагничивающего контура находится вне структуры ЭДС E, которая в полном соответствии с законом электромагнитной индукции "сосредоточена" в элементе X - в катушке без потерь (1).

На наш взгляд выражение (6) должно иметь другой вид, а именно:

U= RI + j X I = RI + E. (7)

При более строгом подходе следовало бы учесть и величину R, а также величину ЭДС самоиндукции E. Тогда основное уравнение трансформатора в режиме реального холостого хода следует записать в виде:

U= (R+R)I+ jX I = RI+ E+ E. (8)

Угол между I и Ф называют углом магнитных потерь. Можно дать следующее физическое истолкование угла отставания магнитного потока от тока холостого хода. Поскольку ток по отношению к потоку первичен, то, скорее всего, намагничивание стали (т.е. создание магнитного потока Ф) происходит лишь после того, как электромагнитная энергия первичной обмотки компенсирует соответствующие потери в стали. Возможно поэтому, ЭДС E реально отстает от вектора потока не на угол π/2, как это общепринято, а на меньший, равный разности между π/2 и углом магнитных потерь.

Если все же полагать, что векторы U и E находятся в противофазе, что более привычно для читателя, то разницу их следует учесть в виде суммы ЭДС самоиндукции E= - jXI , ЭДС взаимоиндукции и падения напряжения на активном сопротивлении намагничивающего контура RI. Уравнению (8) соответствует векторная диаграмма, представленная на рис. 2,а, в которой вектор падения напряжения RI следует заменить на вектор RI.

Схему замещения трансформатора или асинхронной машины в режиме холостого хода можно представляют в известном виде, используя традиционные обозначения "индуктивных сопротивлений" X и X (рис.3,а). Представляется, однако, что более наглядным и более достоверным с точки зрения физической природы явлений в трансформаторе и машинах переменного тока является схема замещения с использованием источников ЭДС E и E (рис. 3,б).

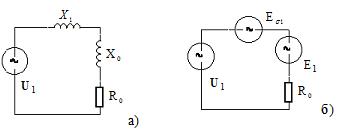
Рис.3. Схемы замещения трансформатора и асинхронной машины в режиме

холостого хода в традиционном и уточненном обозначениях

Выводы. Общепринятые допущения при анализе идеализированных трансформаторов и асинхронных машин в режиме холостого хода некорректны, поскольку приводят к противоречию с законами электротехники и исключают протекание физических процессов в таких машинах. Следовательно, идеализированные в общепринятом плане машины физического смысла не имеют. Такие допущения влекут за собой некорректные основные уравнения, векторные диаграммы и схемы замещения машин в режиме холостого хода, которые приводят к некорректному анализу машин и в режиме нагрузки. Двухобмоточный трансформатор или асинхронная машина имеют как бы третью обмотку, которая представляет собой интегральный контур его магнитопровода. Предложенные с учетом этого обстоятельства уточненные уравнения, векторные диаграммы и схемы замещения более соответствуют реальным физическим процессам в электрических машинах, чем общепринятые.

Литература:

1. Иванов-Смоленский А.В. Электрические машины.-М. Энергоиздат, 1981.