Технические науки.Энергетика

 

Магистрант Конысова.А.О, профессор Айталиев Е.С.

Западно-Казахстанский аграрно-технический университет имени Жангир хана, Казахстан

СТАТИСТИЧЕСКИЕ МЕТОДЫ О ВОПРОСАХ ПРИЕМОЧНОГО КОНТРОЛЯ И АНАЛИЗ СТАНДАРТНЫХ НОРМ КАЧЕСТВА КОНТАКТОРОВ И ПУСКАТЕЛЕЙ

 

В современном производстве массовой продукции широкое распространение получил выборочный (статистический) контроль качества готовых изделий. При выборочном контроле необходимо по качеству проверенной части изделий сделать заключение о качестве изделий всей партии или о качестве технологического процесса. Контроль износостойкости контакторов и пускателей, очевидно, может быть только выборочным из-за его разрушительного характера.

Процедура статистического контроля предъявленной партии продукции состоит из трех последовательных этапов:

-          извлечение выборки из предъявленной на контроль партии продукции;

-   проверка параметров изделий в выборке;

-   принятие решения о качестве предъявленной партии продукции.

Специальные испытания контакторов, пускателей на коммутационную износостойкость носят разрушительный характер, т.е. приводят к полной или частичной потере качества изделий, подвергшихся испытаниям. Такие испытания проводятся, например, для пускателей серии ПМ12 в соответствии с требованиями технических условий и стандартов методом двухступенчатого выборочного контроля. Преимущество двухвыборочного метода здесь состоит в том, что при его использовании необходимо в среднем меньшее число наблюдений, чем при одновыборочном плане с той: же жесткостью контроля. Это приводит к экономии средств, затрачиваемых на процедуру контроля, а также к уменьшению числа изделий, вышедших из строя в результате разрушительного характера испытаний.

По требованиям двухступечатные испытания проводятся на трех пускате-лях/контакторах (численность первой выборки n1=3). Результат испытания считают положительным, если отказов нет. Это означает, что для первой выборки приемочное число Ас, принято равным нулю. Аппараты признают не выдержавшими испытания, если число отказов с1 удовлетворяет неравенству d Rе1, где Rе1 — браковочное число первой ступени. Если число несоответствующих единиц в первой выборке лежит в интервале Ас1 < d < Rе1, то необходимо контролировать вторую выборку (численность которой п2=3), т.е. испытаниям подвергают три дополнительных контактора/пускателя. Число несоответствующих аппаратов, обнаруженных в первой и второй выборках суммируют. Если кумулятивное (суммарное) число несоответствующих единиц продукции равно или меньше приемочного числа второй ступени (Ас2), партию считают приемлемой. Если кумулятивное (суммарное) число несоответствующих единиц продукции равно или больше браковочного числа второй ступени (Re2), партию считают неприемлемой.

Выбор параметров плана контроля качества (n1,Ac1,Re1;n2,Ac2,Re2) может основываться на различных «последующих» оценках. Одной из таких оценок является приемлемый уровень качества AQL (Average Quality Limit), заданный стандартом на контакторы и пускатели на уровне 10% .

Для организации выборочного контроля надо задать систему правил — план контроля, в котором указывается, как и сколько следует отбирать аппаратов для проверки, после какого количества проверенных аппаратов принимать решение о браковке, приемке партий в целом или о дальнейшем продолжении контроля. Такой выборочный контроль, как известно, носит название: приемочный статистический контроль (ПСК).

На практике в большинстве случаев используют методы приемочного статистического контроля по альтернативному признаку, т.е. такой контроль, при котором; каждое проверяемое изделие классифицируется либо как годное, либо как дефектное. Из многих методов ПСК по альтернативному признаку наибольшее распространение получили одноступенчатый (одновыборочный) и двухступенчатый (двухвыборочный) ПСК. Во многих случаях в практике контроля качества предпочитают пользоваться не одновыборочными, а двухвыборочными ПСК, которые имеют некоторые преимущества. Двухвыборочный план обеспечивает в какой-то степени «влияние отсева»: партии с очень высоким или очень низким процентом брака р почти во всех случаях бракуются или принимаются уже на основании первой выборки. И наоборот, окончательное решение о принятии или браковке партий среднею качества принимается лишь по результатам второй выборки.

Использование методов приемочного контроля связано "с риском напрасной браковки хороших партий и риском приемки партий, засоренных дефектными изделиями. При случайном отборе изделий можно при общем небольшом количестве дефектных изделий в партии отобрать на проверку значительное число дефектных, что приведет к ложному решению о браковке хорошей партии (ошибка первого рода). Вероятность такого ошибочного решения - браковки партии качества называется риском изготовителя и обычно обозначается через . С другой стороны, может случиться и так, что при сильной засоренности партии дефектными изделиями в выборке окажется небольшое количество дефектных и плохая партия будет принята (ошибка второго рода). Вероятность такого решения называется риском потребителя и обозначается символом . Однако, риски  и  зависят от доли брака. Указанные риски при выбранных уровнях качества позволяет найти оперативная характеристика.

При р=0 в партии отсутствуют дефектные изделия (L= 1), т.к. партия в любом случае принимается. Если же р = 1, то L= 0, т.к. партия состоит(почти) из бракованных изделий и в любых обстоятельствах должна быть забракована. Таким образом, L есть монотонно убывающая функция в интервале от 0 до 1, - функция L(р).

Построим для требуемого плана контроля оперативную характеристику, согласно формуле 1:

              L(р) = q2+Зpq2q3.                                        (1)

Первое слагаемое в выражении (1) указывает вероятность принятия партии по первой выборке, а второе слагаемое представляет собой вероятность принятия партии во второй выборке, если решение о принятии или браковке партии по первой выборке не было принято.

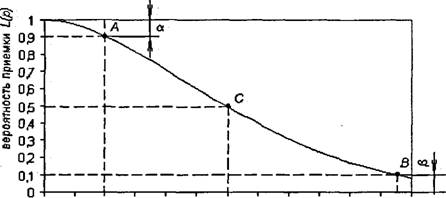
По результатам расчета в соответствии с (1), приведенным в таблице 1 , построен график (рис. 1) оперативной характеристики для данного плана выборочного контроля. Из рис. 1 видно, что вероятность принятия партии резко убывает с ростом засоренности.

Таблица 1 - Оценки стандартного плана контроля контакторов и пускателей

р

q

L(р)

АОQ

0

1

1

0

0,02

0,98

0,995427

0,019909

0,10

0,90

0,906147

0,090615

0,20

0,80

0,708608

0,141722

0,3

0,70

0,494263

0,148279

0,40

0,60

0,309312

0,123725

По оперативной характеристике (рис. 1) определим риск изготовителя.

                         О 0,05 0,1 0,15 0,2 025 0,3 0,35 0.4 0.45 05 0,55 0,6 Т

                                                                                                         доля брака (р)

Рисунок 1 - Оперативная характеристика плана выборочного контроля (3,0,2; 3,1,2): А - приемлемый уровень качества; В - неприемлемый уровень качества; С — точка безразличного качества

 

При заданном стандартом приемлемом уровне качества АQL=0,1 для анализируемого плана контроля получаем следующие значения: риск изготовителя 0,1. Если принять риск потребителя р равным риску изготовителя, положив р = 0,1, то неприемлемый (браковочный) уровень качества по кривой рис. 1 окажется равным p6р =0,577. В зону неопределенности попадают партии с уровнями дефектности 0,1 < рi < 0,577. Кроме приемлемого уровня качества и риска изготовителя аппаратов среди последующих оценок особый интерес представляет величина среднего выходного качества, обозначаемая в стандартах аббревиатурой AOQ (Average Outgoing Quality). Эта величина есть по определению математическое ожидание выходного качества, то есть доля дефектных аппаратов, проникающих к потребителю после контроля. По сути происхождения эта доля U есть дискретная случайная величина. Таблица, описывающая ее распределения для рассматриваемого плана, представлена ниже.

Таблица 2 – Распределение дискретной случайной величины

Событие

Приемка на первой выборке

Приемка на второй выборке

Отказ в приемке

Значение U

p*{N-n1)/N

p*(N-n1-n2)/N

0

Вероятность события

q*q*q

(3*p*q*q)*(q*q*q)

1 -L(p)

 

Предполагая, что во всех случаях. значения численности выборки много меньше численности партии N. найдем оценку AOQ согласно формальному определению математического ожидания в виде суммы произведений значений случайной величины на их вероятности

 

AOQ = q*q*q*p*(N-n1)/N + (3*p*q*q)*(q*q*q)*p-{N-n1 -n2)/N  + +0*(l-L(p))p*(q*q*q*p + (3*p*q*q)*(q*q*q)) = p*L(p).

При изменении доли брака от 0 до 1 монотонно изменяющаяся величина AOQ проходит через максимум, называемый пределом среднего выходного качества. Этот предел в стандартах принято обозначать аббревиатурой AOQL (Average Outgoing Quality Limit). Расчет, приведенный в табл. 1, и график на рис. 2, показывают, что предел среднего выходного качества не превосходит 0,15 (точка С).

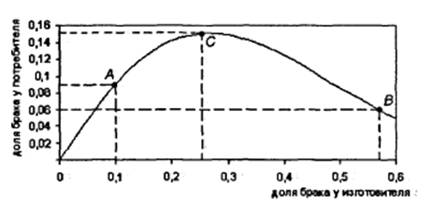
Рисунок 2 – Среднее выходное качество

Таким образом, нами получены практически исчерпывающие оценки стандартного плана контроля контакторов и пускателей, позволяющие аргументировано решать вопросы арбитражных ситуаций.

 

 

 

 

 

 

 

 

Список использованной литературы:

1. Беляев Ю.К. Вероятностые методы выборочного контроля. М.Наука, 1975. – 408 с.

2. Карасев А.И. Теория вероятностей и математическая статистика. М.: Стаистика, 1970. – 344 с.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. 7-е издю стер.- М.: Высш.шк., 2001. – 479 с.