Технические науки/ Авиация и космонавтика

Dr Nickolay Zosimovych

University of South Wales, Pontypridd, UK

STRUCTURAL AND PARAMETRIC OPTIMIZATION FOR FLIGHT VEHICLE STRUCTURES

Keywords: Parametric optimization (PO), technical system (TS), flying vehicle (FV), design and development (D&D), structural optimization (SO), structure diagram (SD), engineering design solutions (EDS), airframe, structural modules (SM), essential features (EF), matrix, unmanned flying vehicle (UFV).

I. Introduction. The parametric optimization (PO) methods enabling us to determine the optimal values of the technical system (TS) parameters for a specified structure have been well developed to date and successfully applied.

Besides optimization of parameters of the designed unit, considerable attention of scientists and practical specialists is attracted to the problem of synthesis of its structure [1-4]. This problem is very important and fundamental, as it is virtually impossible to develop a unit with an ill-conceived and ill-founded structure to a rational design level [5-7]. In its turn, the flying vehicle (FV) structure influences the efficiency of TS [8]. In order to improve technical and economic parameters of the designed product, design and development (D&D) shall be conducted in three stages [4, 9-10]. Specific types of problems shall be solved at each stage.

II. Principles of Design Objects Decomposition. Problems of the first type are the problems of choosing or finding the most effective physical principle of functioning under specified conditions and requirements. In aviation and rocketry, these problems are solved at the stage of general or external design of the flying vehicle. This stage shall result in establishment of a combination of physical and geometrical characteristics, guiding a conceptual design of the flying vehicle. They shall be as well initial data for the next structural design stage solving the problems of the second type. It should be understood that the structural design and designing are not synonyms and are hierarchically interrelated separate stages of design and development (D&D) [1, 4, 12].

The second-type problems are the problems of selection or searching for the most efficient technical solution, when physical operating principle has been specified. Problems of the second type are sometimes referred to as problems of structural optimization (SO). The flying vehicle structure usually means its structure diagram (SD) governed by design features. However, SD ambiguously conditions technical solutions [9]. A technical solution shall be predetermined both by design and technological characteristics. When selecting and validating an efficient technical solution, you should optimize its adaptability to streamlined manufacture [5]. So, FV structure design stage must result in a reasonable choice of engineering design solutions (EDS). Hereinafter, EDS shall mean a structure clearly conditioning the technical solution. The problems of searching rational structures belong to the class of inverse problems. To solve the direct problems we are to study the predetermined structure of an object and determine its physical condition while in order to solve inverse problems we are to synthesize the structure of an object that optimally implements the required physical condition. These problems are not subject to full formalization, since complete set of requirements for EDS cannot be formalized. It is difficult for example to formalize the requirement of adaptability, ease of operation, etc. In these conditions it is necessary to develop systems of models which should simulate FV function and the designer dialogue with the simulated models. These problems are rather scientific than technical ones [1].

The detailed EDS elaboration to the level corresponding to the execution plan shall be done at the design stage while solving problems of the third type. The designing purpose is materialization of EDS.

The third type of problems includes problems of determining the optimum design and technical parameters for the given technical solution. The result from solving these problems in the design stage shall be a set of design, engineering, technical and other documents required by the standards.

The hierarchical structure of D&D problems becomes apparent with a possibility of step-by-step solution. It demonstrates that problems may be not merely split into simpler ones but also that there are qualitative changes in the problems occurring during transition between one stage and the next one. Another feature of the hierarchical structure is a close relationship between designed subsystems. It does not allow completing the design in one cycle, and makes it necessary to build an iterative design process.

Apparently each D&D stage is characterized by its own level of structure development. If we present the airframe structure of FV as a tree graph with the entire set of detailed structural features [13], then iterative design procedure will turn dimensionality problem into what Bellman called "curse of dimensionality" [1, 4].

Under these conditions, the solution of problems at any design stage encounter two difficulties [1, 13]:

1) there are too many variables; for FV the vector dimensions are to be within 10³…10⁶;

2) structural variables at different levels influence the functional properties of the structure too differently, which certainly results in a large number of inefficient search steps.

Therefore, it is necessary to have harmonized decomposition design problem schemes and design object structures.

Creation of harmonized decomposition schemes for object structures and design problems reduces the dimensionality problem and allows us to choose the structure and characteristics of load-bearing units not only from the standpoint of efficiency of the units, as it often happens in practice, but also considering their joint operation in the designed flight vehicle. This should significantly increase the efficiency of EDS due to reduction of time, cost and complexity of experimental testing of flight vehicle’s design elements. In order design tests could be verification of the design, rather than an improvement means, you must submit to the tests a design implementing a reasonable technical solution [14].

III. Decomposition of Flight Vehicle Structures. Let’s define the structure of TS and formalize it in relation to the subject area of research, i.e. FV [8, 15, 16].
From the engineering point of view different structures of TS under consideration differ from each other by the number of elements, the elements themselves and the method connecting these elements. From the mathematical point of view, there are different PO problems for different structures. If you can’t specify same sets of optimized parameters, the same objective functions and limits when stating PO problems for two TS versions, these TS versions have different structures [7, 11]. It is easy to note that this definition of the structure does not contradict the engineering sense. Let’s describe this concept, based upon the information about the product contained in the structure.

The structure of the product determines its properties, which ensure operation of the product with high reliability, and which may be provided to it during the manufacturing process. This definition general for TS applies as well to the concept of flying vehicle structures but requires more detailed consideration.

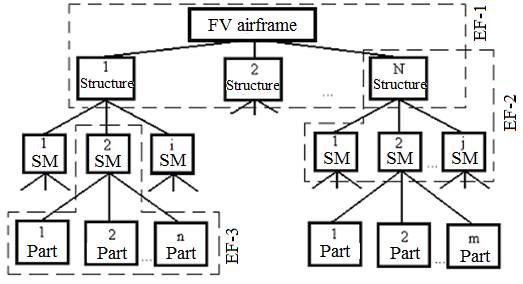
Fig. 1. Functional and constructional modules of structures included into FV airframe

When we design the structure of a flying vehicle airframe, we deal with a complex TS hierarchically subdivided into simpler assembly units [13]. So, for example airframe functionally and structurally consists from several FV structures, which in their turn are subdivided into units – structural modules (SM), and each of the lower-level units consists of technologically inseparable parts (Fig. 1) [16].

The assembly units are products with their specific functional properties. It means they have their own structures implementing these properties. Obviously, the principle of structure decomposition must be general for all levels of scheme decomposition (see Fig. 1). It should bring in line common design and engineering laws specific for FV airframe design with the functional properties of the structure at each decomposition level.

The suggested decomposition of FV structures is based on the principle of identification of the essential features (EF) in the structure, and their localization at each level of the decomposition scheme [3, 4, 13]. The idea to identify the essential TS features and to establish the relationship between them can significantly accelerate finding the best solution in order to improve the quality of the design process itself [7, 10, 17].

Table 1

Matrix for essential feature groups according to their influence upon different functional characteristics of the object

Level of study	TS function	Performance capabilities
		FV airframe	units	SM
1
2
3
4

We can establish several groups of EF as relates their influence on the various functional properties of the object (Table 1.) in the structure of assembly units for airframe of an unmanned flying vehicle (UFV) [1, 13]. These properties should include [18]:

· functioning of the object as TS with well-defined tasks;

· functioning (performance capabilities) of the object and its constituent elements under the influence of the environment.

Table 1 [13, 16, 19] represents a triangular SM matrix. The main elements of the matrix (), which represent a group of EF, which is established during the analysis of the relevant functional design properties are to be found at the intersection of lines (levels of study) and columns (functional properties). All the structural features designated in the columns represent the structure at the referred level of study.

Structural features are generalized structural parameters hierarchically adjusted according to decomposition levels with progressive detailed elaboration to the level corresponding to the design concept. At each level of the structure decomposition we can identify three groups of structural features [1, 3, 18]:

1) physical and mechanical characteristics of construction materials;

2) geometric parameters with technological and operational limitations;

3) mass and inertial characteristics.

Hence, the structure at each level of decomposition scheme will be determined by three sets of parameters [14, 16]:

The first group is parameters, which are invariable during the analysis and synthesis of the structure. The second groupare the geometric parameters variable within the prescribed limits:

where and are the minimum and the maximum values determined based on technical and operational conditions.

Table 2

Topology levels of structure development

Structure decomposition level	Complex of varying characteristics	Decomposition of structure topology
1		External topology of FV structures
2		Internal topology of FV structures
3		External SM topology
4		Internal SM topology

Table 3

Formalization of the structure decomposition of FV structures

Structure decomposition level	Structure decomposition of FV structures
1	- structural and technological division of the airframe
2	- airframe structure
3	- structure composition
4	- structural and technological solution

The third group are the parameters derived from the first and the second groups. All the varying characteristics at the structural levels represent the level of development of the structure topology. (Table 2) [12, 14, 18].

So, if we summarize the above and complement definition of the structure with a requirement of the minimum FV weight requirement, it will be possible to give a definition of the structure general all levels of decomposition [18, 19]. The FV structure consists of a set of structural features (providing the structure with physical, mechanical, technical and operational properties), which will ensure a highly reliable operation of the designed unit, conditioned upon minimum weight of the FV [8, 13].

The above analysis of structural components according to their influence on the functional properties of the FV, allows us to formalize the structure decomposition of FV structures (Table 3) [3, 16, 18].

Conclusion. Thus, the structure decomposition of FV structures is based upon identification of essential features that reflect the specific structural and technical patterns for structure formation and adjustment with specific functional properties of FV [13, 19]. Such structure decomposition is not an artificial device decreasing dimensions. It is caused by the difference in operational requirements for the airframe in general, its units and structural modules. For example, if the requirements for strength and stability of the SM, which make up the structural units (compartment housing, the bearing surface), are fulfilled, there will remain the problem of overall stability (static and dynamic) of the FV structures. At the same time, operability of units is a necessary but not sufficient condition for the FV airframe operation, since implementation of the operational requirements for the design of the FV in general associated with harmonization of the elastic behavior, mass and inertial properties of the units.

References

1. Голубев И.С., Андреев В.В., Парафесь С.Г. Методы структурно-параметрической оптимизации силовых авиационных конструкций: Учеб. пособие. – М.: Изд-во МАИ, 1991. – 68 с.

2. Зосимович Н.В. Декомпозиция задач синтеза структуры силовых конструкций ДПЛА для оперативного природоресурсного и экологического мониторинга окружающей среды // Cборник научных трудов по материалам научно-практической конференции «Научные исследования и их практическое применение. Современное состояние и пути развития», 1-15 октября 2005 г. Том 8. Технические науки, сельское хозяйство. – Одесса: Черноморье, 2005.- C.9-13.

3. Первозванский А.А., Гайцгори В.Г. Декомпозиция, агрегирование и приближенная оптимизация. М.: Наука, 1979.

4. Лось Л.В. Теория структуры конструкций технологичных машин и приборов. – Житомир:. Житом. сельскохоз. ин-т, 1991. – 167 с.: ил.

5. Бирюк В.И., Липин Е.К., Фролов В.М. Методы проектирования рациональных конструкций ЛА // Труды ЦАГИ, № 1776, 1976.

6. Ланцош К. Практические методы прикладного анализа. М.: Физматгиз, 1961.

7. Валуев М.И., Харченко В.П., Яппаров А.Н. Системотехніка та основи проектування аеронавігаційних систем: Навч. Посіб. – К.: НАУ, 2003. – 120 с.

8. Беспилотники / Аэрокосмический вестник. – 2005. - № 8. – К.: ООО «СПЕЙС-ИНФОРМ», с. 32-33.

9. Половинкин А.И., Бобков Н.К., Бум Г.Я. Автоматизация поискового конструирования. – М.: Радио и связь, 1981.

10. Половинкин А.И. Автоматизированные системы поискового конструирования // Материалы І Всесоюзного совещания по автоматизации проектирования в машиностроении. АН БССР, Минск, 1978.

11. Дитрих Я. Проектирование и конструирование. Системный подход. – М.: Мир, 1981.

12. Вязгин В.А., Федоров В.В. Математические методы автоматизированного проектирования. М.: Высш. шк., 1989.

13. Зосимович Н.В. Структурно-параметрическая оптимизация силовых конструкций дистанционно-пилотируемых летательных аппаратов оперативного природоресурсного и экологического мониторинга окружающей среды // Региональный вестник молодых ученых. М.: Academa, 2005.- №3.- C. 97-98.

14. http://www.mai.ru/conf/aerospace/internetconf/ - Парафесь С.Г. Использование математического аппарата идентификации конструкций в задачах проектирования летательных аппаратов // Интернет-конференция "Авиация и космонавтика-2007"

15. Зосимович Н.В. Методика решения декомпозиционных задач синтеза структуры силовых конструкций ДПЛА для оперативного природоресурсного и экологического мониторинга окружающей среды // II Международная периодическая научно-практическая конференция «Альянс наук: ученый – ученому», 3-7 октября 2005 г. Том. 3. – Днепропетровск: НАЦ «Ера». - C. 39-44.

16. Зосімович М.В. Структурно-параметрична оптимізація силових конструкцій дистанційно-пілотованих літальних апаратів для оперативного природоресурсного та екологічного моніторингу довкілля // Вісник Національного авіаційного університету. - № 3-4 (33). – К.: НАУ, 2007. – С. 127-132.

17. Левин Г.М., Токаев В.С. Декомпозиционные методы оптимизации проектных решений. – Минск: Наука и техника, 1978.

18. Зосимович Н.В. Задача декомпозиции структуры силовых конструкций ДПЛА для природоресурсного и экологического мониторинга окружающей среды // Матеріали VIIІ Міжнародної науково-практичної конференції “Наука і освіта’2005”, 20-30 червня 2005 р. Том 53: Технічні науки. Дніпропетровськ: Наука і освіта, 2005.- C.14-17.

19. Зосимович Н.В. Математические основы проектирования ДПЛА экологического назначения // Стратегія розвитку України, К.: НАУ, 2006. - № 5.– C. 218-222.