К

Россия, Кабардино-Балкарский государственный аграрный

университет имени В.М.Кокова, Россия

Буздов М.А.

Кабардино-Балкарский государственный

университет имени Х.М.Бербекова, Россия

Определение параметров биоткани при криохирургической операции в области формы полукольца.

Криохирургическая операция состоит в уничтожении клеток в ограниченном объеме биоткани, занимаемом злокачественной опухолью. Гибель клеток достигается в результате разрыва мембран образующимися при криогенном охлаждении кристаллами льда внеклеточной и внутриклеточной жидкости, а также осмотического разбухания при оттаивании биоткани. Поэтому актуально математическое моделирование тепловых процессов в замораживаемой биоткани, требующее разработки эффективных методов решения задач типа Стефана, особенностью которых в криобиологии является пространственная локализация и существование предельных стационарных решений.

Биоткань может охлаждаться криохирургическими инструментами различной формы (плоской, цилиндрической, конусообразной и т.д.). В случае, когда охлаждающая поверхность криоинструмента имеет довольно большую длину, пренебрегая вкладом в распределение температуры координатой Z (ось OZ считаем параллельной оси инструмента), мы получаем двумерную начально-краевую задачу типа Стефана. Будем считать, что криоинструмент имеет цилиндрическую форму, а область, в которой будем искать распределение температуры, имеет форму полукольца.

Постановку задачи, в связи со сказанным выше, удобней будет сделать, введя полярные координаты

x=r cosj, y=r sinj,

где r - полярный радиус, а j - полярный угол. Тогда уравнения, описывающие процесс теплообмена в указанной выше области будут следующими:

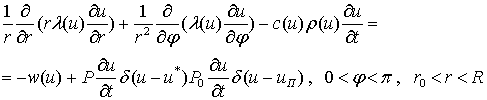(1)

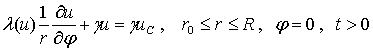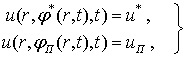(2)

Здесь j^*(r,t), j_П(r,t) - изотермические поверхности, на которых температура биоткани равна u^* и u_П соответственно; r₀ - радиус цилиндрического криозонда; R - некоторая известная постоянная величина, характеризующаяся тем, что вне полукруга радиуса R температура биоткани постоянна и равна .

Определению подлежат функции u(r,j,t), j^*(r,t), j_П(r,t). Будем считать, что коэффициенты c(u), r(u), l(u) могут иметь разрывы при и что выполнены условия C(u)³C_min>0, r(u)³r_min>0, l(u)³l_min>0. Для решения поставленной выше задачи предлагается следующий алгоритм.

Вводим функцию

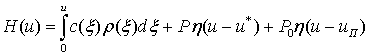после чего уравнение (1) можно переписать в виде:

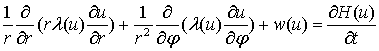(3)

Далее проводим сглаживание функций H(u), l(u), после чего получаем последовательность ограниченных гладких функций H^k(u), l^k(u), сходящихся при , соответственно к H(u), l(u), причем:

B^k(u)=H^k(u)³c=const>0. (4)

Задачу Стефана (1), (2) можно теперь заменить аппроксимирующей «сглаженной» задачей, для которой и будет строиться численный алгоритм:

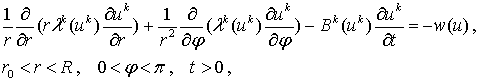(5)

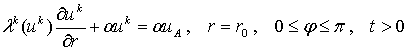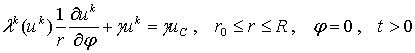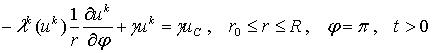Условия (2) на изотермических поверхностях при такой постановке содержатся в уравнении (5). Для решения данной задачи применяется локально-одномерный метод, что можно делать и в случае полярных координат (см.[1]). Прежде чем выписывать разностную схему, введем в рассматриваемой нами области пространственно-временную сетку. Для простоты будем рассматривать равномерные сетки по каждому из направлений.

Обозначим:

где

r_N=R, r₀=r₀;

где

j₀=0, j_М=p;

, где .

Тогда на множестве вместо функции непрерывных аргументов u(r,j,t) будем рассматривать функцию дискретных аргументов , значения которой вычисляются в узлах сетки . Обозначим . Для сеточной функции получаем следующую разностную схему:

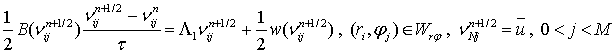
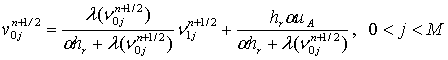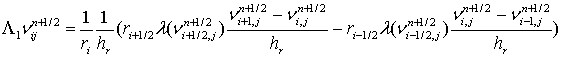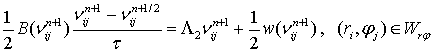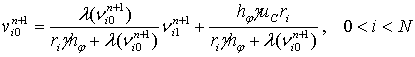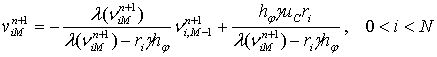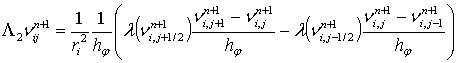Здесь

У функций B^k, u^k, l^k для наглядности индекс k опущен. Для нахождения значений сеточной функции n на (n+1)-м временном слое по известному значению на n-м временном слое необходимо последовательно решать две серии одномерных задач, соответственно по координатам r и . Каждая такая задача представляет собой нелинейную алгебраическую систему с трехдиагональной матрицей, и для ее решения используется метод прогонки совместно с итерационным методом Ньютона. При этом при определении nⁿ⁺¹ коэффициенты c, r, l, берутся на предыдущей итерации [2]. Возвращаясь к исходной задаче (1), (2), предложим описанный в [4, 4] способ нахождения граничного условия, когда коэффициент g теплообмена с окружающей средой неизвестен. Для этого для каждого момента времени t_n=nt решается следующая одномерная краевая задача:

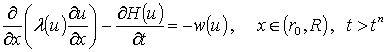Функция u=u(x,t), являющаяся решением этой задачи и будет задавать граничное условие (уже 1-го рода) для задачи (1), (2). Для отрезка [-R,r₀] решается аналогичная последовательность одномерных задач. Описанный выше способ нахождения граничного условия точнее отражает реальность, так как тепло особенно быстро распространяется вдоль поверхности биоткани.

В постановке обратной задачи по определению, наряду с искомыми в прямой задаче функциями, какого-либо постоянного параметра в уравнении или краевых условиях дополнительно присутствует условие:

u(r_Д,j_Д,t_Д)=u_Д , r_ДÎ(r₀,R), j_ДÎ(0,p), t_Д>0. (6)

Предлагаемый метод решения применим, когда определяемый параметр зависит от значения u_Д монотонно. Подобная зависимость коэффициентов теплообмена a и g, а также параметра нелинейности b из (1) вытекает из физического смысла задачи, что подтверждается и при расчетах. При этих условиях обратная задача решается с использованием метода решения соответствующей прямой задачи. А именно, при различных значениях искомого параметра решается прямая задача до тех пор, пока значение вычисленной функции с достаточной точностью не совпадет со значением из условия (6). Порядок изменения параметра можно осуществлять различными способами. Например, методом половинного деления.

Литература:

1. Калиткин Н.Н. Численные методы. М., Наука, 1978.

2. Самарский А.А., Моисеенко Б.Д. Экономичная схема сквозного счета для многомерной задачи Стефана. ЖВМ и МФ, 1965, т.5, №5, с. 816-827.

3. Буздов Б.К. Численно-аналитические методы решения двумерных задач типа Стефана в криомедицине. – Дис. канд. физ.-мат. наук. – Киев, 1995.

4. Буздов А.К. Конструктивные методы решения задач со свободными границами в проблемах криомедицины. - диссертация на соискание ученой степени кандидата физико-математических наук / Нальчик, 2000.