Mathematics / 1.

Sraichuk I.R.

Kryvyi Rih National University, Taras Shevchenko National University of Kiev

Scientific supervisor M.O. Rashevs'kyi, Ph.D.

About the Asymptotic Solutions of a Linear System of Integro-differential Equations

Let’s consider a system:

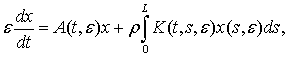(1)

where x(t, e) is required vector, n is dimensional vector, A(t, e) and K(t, s, e) – n x n are matrices, which are represented by convergent series according to degrees of small parameter e >0: 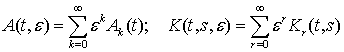. Asymptotic solutions of the Cauchy problem:

x(0, e) = x₀ (2)

in the interval t Î [0, L], L < ¥ for the system (1) it will be depending on the secular equation roots:

det(A(t, 0) - lE) = 0 (3)

A number of studies deal with the case where roots of given equation (3) change the order in individual points – the turning points [1] or if there are other unstable states [2] of matrix spectrum A(t,0). In scientific publications [3] and [4] the integration method of the weak nonlinear system with appropriate Hermite matrix A(t, 0) and with nearly diagonal matrix A(t, e) is proposed.

In this study, the method mentioned in publication [3] is used for tasks (1), (2) with nearly diagonal matrix A(t, e). We will require the following conditions:

1. Matrices A_p(t) and K_p(t, s) are indefinitely differentiable in the interval [0;L] and in the square D = {0 £ t, s £ L}; p ³ 0.

2. Roots of secular equation (3) are different, when t Î (0, L] and the same when t = 0.

Formal solution of the system (1) will be in the form:

(4)

where z(t, e) - n is dimensional vector, U(t, e) and P(t, s, e) – indeterminate n x n –matrices.
When substituting expression (4) in equation (1), after interchange of integration in iterated integral, we obtain:

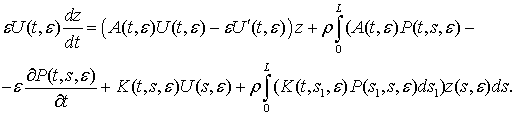
Matrices U(t, e) and P(t, s, e) will be built to keep the equations

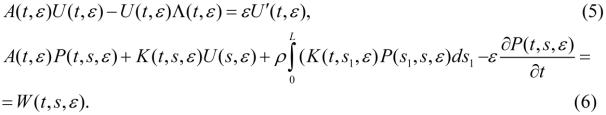
Matrix W(t,s,e) will be mentioned later. The construction of matrices U(t,e) and P(t,s,e) essentially depends on character of unstable states of matrix spectrum A0(t).

Let’s analyze nearly diagonal matrix A(t,e). The condition is as follows:

3. A₀(0) is zero matrix.

The last condition implies the existence of nonsingular T (t) where

T ^-1A₀(t)T = diag {l₁(t), l₂(t), …, l_n(t)} = L(t); L(0) – zero matrix. In this case the singular system, derived from (1), when e=0 will have solutions in the class of generalised functions [5].

Let’s build indeterminate matrices in the form of 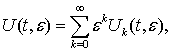To satisfy the equation (4), matrix system will be solved by using the method [1].

Equating the coefficients with equivalent order of ε in equation (5), we will obtain the infinite system of matrix integral equations

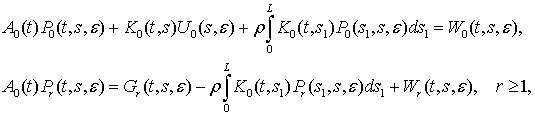
These systems are Fredholm’s systems of integral equations of the third kind, which have the form 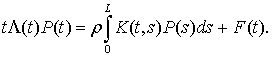We will build the solution of the last equation in the form: P(t) = Cd_p(t) + Y(t), where C – constant matrix, d _p(t) – «right delta» [5], Y(t) – matrix with indiscrete elements. Substituting matrix P(t) to the system, we will obtain the equation 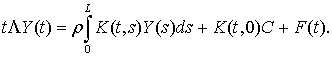If t = 0 in this equation we obtain: 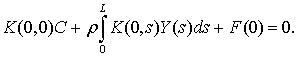From the last equation we find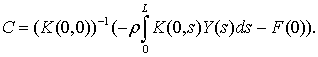

After this definition of C matrix we will find Y(t) from the system which is a Fredholm’s system of the second kind with indiscrete coefficients ( t = 0 – point of removable discontinuity). Let Y(t) is indiscrete solution of the last equation.

Matrix C will be zero matrix, if

On this basis, we will build W_k(t, s, e), to provide indiscrete elements of matrix P_k(t, s, e).

The indeterminate vector z(t,e) will be obtained from the system

,

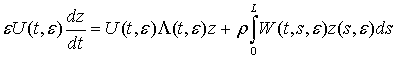initial data from the equation.

Applying equation [3] to the last system we will prove next theorem.

Theorem. If conditions 1.-3. are fulfilled and functions Re(l_i(t) - l_j(t)) in the interval of asymptotic solutions don’t change the sign, than the task (1),(2) has formal solution in the form equation (4), moreover for some exact solution x(t, e) and received from (4) m-approximating x_m(t, e) (x_m(0, e) = x₀) the following equation is realized

,

where C - constant, which depends on e, q - the order of turning point.

References:

1. Wasow W. Linear Turning Point Theory. – N.Y.: Acad. Press, 1985. – 246 p.

2. Бободжанов А.А., Сафонов В.Ф. Метод нормальных форм в сингулярно возмущенных системах интегро-дифференциальных уравнений Фредгольма с быстро изменяющимися ядрами // Матем. сб., 204:7 (2013), с. 47–70

3. Grimm L.J., Harris W.A. Solutions of a singularly perturbed differential system with turning points // J. Fac. Sci. Univ. Tokyo. Sec I. A.- 1989. - 36, №3.- P. 753-763.

4. M.O. Rashevs'kyi. Asymptotic Integration of Weakly Nonlinear Systems with Unstable Spectrum // Nonlinear Oscillations - 2002. – 5, № 4. - P. 512-522.

5. Иманалиев М.И. Обобщенные решения интегральных уравнений первого рода. - Фрунзе: «Илим», 1981. – 144 с.