Доктор физ.- мат. наук, доцент А. В. Макаричев, А. А. Кудь, А. Б. Щукин

Московский государственный университет им. М.В. Ломоносова

Харьковский национальный автомобильно-дорожный университет Национальный аэрокосмический университет «ХАИ»

СУММЫ В МНОГОЛИНЕЙНОЙ СИСТЕМЕ МАССОВОГО ОБСЛУЖИВАНИЯ БЕЗ ОЖИДАНИЯ С УПРАВЛЯЕМЫМ СЛУЧАЙНЫМ ПРОЦЕССОМ ВХОДНЫМ ПОТОКОМ ТРЕБОВАНИЙ

В систему массового обслуживания поступает входящий поток требований с параметром , который зависит от траектории случайного процесса на отрезке времени , . Предположим, что в момент времени система свободна от требований.

С каждым поступающим в систему требованием связано случайное приращение с функцией распределения , моментами и характеристической функцией

.

Обозначим - число поступивших в систему требований на отрезке и

.

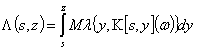Тогда распределение случайной величины имеет вид

,

Характеристическая функция суммы независимых одинаково распределенных как случайных штук слагаемых

имеет вид

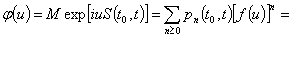
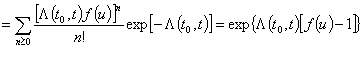
Дифференцированием в нуле функции определяем математическое ожидание суммы

и ее дисперсию

Требования в системе массового обслуживания обслуживаются без ожидания. Обозначим через функцию распределения времени обслуживания пришедшего в момент времени требования.

Пусть - число требований, завершивших свое обслуживание в системе на отрезке времени , и

.

Тогда распределение случайной величины имеет вид

,

Характеристическая функция суммы независимых одинаково распределенных как случайных слагаемых

имеет вид

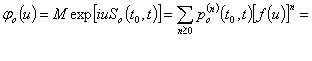
Дифференцированием в нуле определяем математическое ожидание суммы

и ее дисперсию

.

Пусть - число требований, не завершивших свое обслуживание в системе на отрезке времени , и

.

Тогда распределение случайной величины имеет вид

,

Характеристическая функция суммы независимых одинаково распределенных как случайных слагаемых

имеет вид

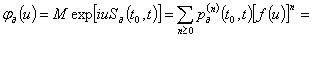
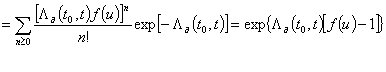
Дифференцированием в нуле определяем математическое ожидание суммы

и ее дисперсию

.

Литература.

1. B. V. GNEDENKO AND I. N. KOVALENKO, Introduction to Queueing Theory, Program for Scientific Translations, Jerusalem, 1968.

2. Климов Г. П. Стохастические системы обслуживания, М., 1966, 244 с., ил.

3. Соловьев А. Д. Асимптотическое поведение момента

наступления редкого события в регенерирующем процессе.

Известия АН СССР. Техническая кибернетика, 1971, № 6, с.

79-89.

4. Вопросы математической теории надежности /Е.Ю.

Барзилович, Ю.К. Беляев, В.А. Каштанов, И.Н. Коваленко,

А.Д. Соловьев, И.А. Ушаков; Под ред. Б. В. Гнеденко.- М.:

Радио и связь, 1983.- 376 с., ил.

5. Хинчин А. Я., Работы по математической теории массового

обслуживания, Москва, Физматгиз, 1963, 236 с.

6. Ширяев А.Н. Вероятность, М.: Наука, 1980, 576 c.