Нелинейное моделирование динамики орбитальных стационарных точек фотогравитационной ограниченной задачи трех

А.Т. Турешбаев, Мырзахметова С.Е.

Рассматривается фотогравитационная ограниченная задача трех тел, в которой оба основных тела являются источниками излучения световой энергии. Проводится нелинейное исследование устойчивости треугольных точек либрации в плоской задаче с учетом резонансных режимов 3-го и 4-го порядков. Показано, что в области устойчивости линейной системы всюду имеет место устойчивость по Ляпунову за исключением резонансного множества точек, в которых может быть нарушена устойчивость

Движение частицы пренебреженно малой массы будем изучать в поле двух гравитирующих и одновременно излучающих тел и , считаемых материальными точками, и, обращающихся друг относительно друга по круговой орбите. Тогда движение частицы задается каноническими уравнениями 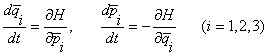[1]

, (1)

где суть декартовые координаты частицы , - соответствующие канонические импульсы, а - аналитическая функция Гамильтона относительно координат и импульсов, которая в нашем случае имеет вид

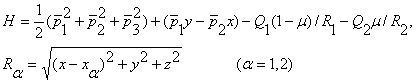(2)

Здесь и - коэффициенты редукции масс основных тел.

В уравнения (1) вводим возмущения по формулам

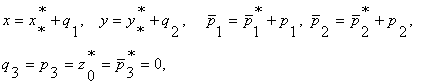(3)

и раскладывая гамильтониан в ряд по степеням возмущений и в окрестности рассматриваемой точки, принимаемой за начало координат, получим

(4)

(5)

(6)

(7)

где , , коэффициенты [1], зависящие в сложной форме от массового параметра и и .

Полагая, что в системе отсутствуют резонансы 3-го и 4-го порядков, после применения преобразования Биркгофа, и ограничиваясь разложением до четвертого порядка включительно, функцию Гамильтона можно записать в виде

(8)

Согласно теореме Арнольда-Мозера [2] при одновременном выполнении условий

(9)

(10)

где - целые числа, удовлетворяющие условию (- порядок резонанса), а - коэффициенты нормальной формы, зависящие от частот и линейной системы, для всех значений массового параметра m из области устойчивости линейной системы всюду сохраняется устойчивость по Ляпунову исходной системы (1). Исключение составляют множества точек, отвечающие резонансам 3-го и 4-го порядков.

При резонансе нормализованный гамильтониан примет вид

(11)

где

при положительных значениях и нигде не обращается в нуль. Откуда следует, что в ограниченной фотогравитационной задаче трех тел в области устойчивости линейной системы треугольные точки либрации всюду устойчивы по Ляпунову, за исключением множества точек, определяемого соотношением (9), для которых реализуется резонанс третьего порядка.

При наличии в системе резонанса четвертого порядка нормализованный гамильтониан в полярных координатах примет следующий вид:

Здесь .

Следует заметить, что если в классической задаче для конкретного значения m коэффициенты и принимают постоянные значения (что намного упрощается исследование задачи), то в фотогравитационной задаче эти же коэффициенты не остаются постоянными и являются функциями координат x, y или и , вследствие чего задача резко усложняется. Используя результаты А.П. Маркеева [2] получим, что при резонансе четвертого порядка , определяемого множеством точек из области устойчивости линейной системы, треугольные точки либрации при

а) - устойчивы по Ляпунову, в) - неустойчивы, (12)

где .

Здесь коэффициенты , являющиеся инвариантами функции Гамильтона (4) относительно канонических преобразований, зависят от коэффициентов однородных полиномов (6-7) степени m (m=3, 4), которые в нашем случае являются функциями параметров системы - коэффициентов редукции и и безразмерной массовой μ.

Вследствие громоздкости выражений этих коэффициентов, полученных в результате нормализации, исследования проводились на компьютере при помощи специально разработанной программы.

Результаты нелинейного компьютерного моделирования показали, что для всевозможных значений параметров системы треугольные точки либрации на резонансном множестве точек 3-го порядка в обобщенной фотогравитационной ограниченной задаче трех тел всегда неустойчивы.

Построены области устойчивости треугольных точек для значения массового параметра μ=0,01 (рис.1,2). Установлено, что в этом случае (при μ=0,01) резонанс 3-го порядка не реализуется. Найдены участки области, соответствующие резонансу 4-го порядка , где выполняется неравенство, что свидетельствует об устойчивости по Ляпунову исследуемых точек либрации в плоском варианте задачи (в случае пространственной задачи имеет место устойчивость в 4-ом порядке); на других участках области, где неравенство меняет знак на обратной, имеет место неустойчивость исследуемых точек.

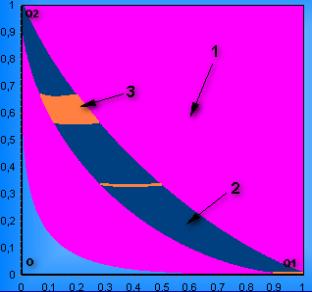
Рис.1. Область устойчивости при резонансе 4-го порядка (μ=0,01) 1 - область устойчивости в линейном приближении; 2 – устойчивость; 3 – неустойчивость.

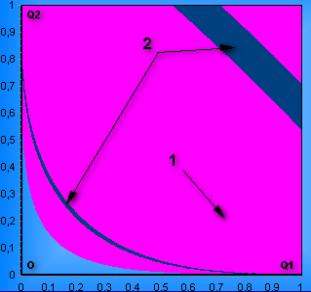
Рис. 2. Область устойчивости при (μ=0,01) 1 - область устойчивости в линейном приближении; 2 – неустойчивость.

Указаны области (рис.2), в которых условие (10) не выполняется. В области устойчивости в первом приближении треугольные точки в плоской задаче трех тел всюду устойчивы по Ляпунову за исключением, быть может множества точек, в которых реализуются резонансы , , и не выполняется условие теоремы Арнольда-Мозера. Следовательно, вопрос об устойчивости треугольных точек либрации в плоской фотогравитационной ограниченной задаче трех тел решен до конца.

Литература

1. Пережогин А.А., Турешбаев А.Т. Об устойчивости треугольных точек либрации в фотогравитационной задаче трёх тел // Астрон. журн. 1989, Т.66. С.859-865.

2. Маркеев А.П. Точки либрации в небесной механике и космодинамике. М.: Наука. 1978. 312 С.