В.В.Подгорная
Минск,
Учреждение образования Федерации профсоюзов Беларуси «Международный институт
трудовых и социальных отношений»
Методика работы по теме «Производная» при изучении
курса высшей математики для экономических специальностей вуза
При изучении курса высшей математики все
предлагаемые задачи заставляют студентов глубоко и целенаправленно мыслить,
находить пути решения, т.е. выстраивать алгоритмы трудных задач. Предлагая
решить ту или иную задачу, мы проверяем не только знание студентами стандартных
математических формул и основных понятий, хотя эти знания первичны и
необходимы, но и способность обучаемых мыслить. Таким образом, решение
математических задач – это нахождение способа выхода из ситуации, сложенной
неопределенностями. Такую способность специалистов называют сейчас
компетентностью, без которой сложно работать в условиях рыночной экономики.
Рассмотрим некоторые методические приемы, позволяющие
эффективно обучать студентов решению задач по высшей математике:
самостоятельная домашняя работа, решение задач по образцу, групповая
самостоятельная работа во время семинарского занятия. Продемонстрируем данные
приемы на примере изучения темы «Производная и дифференциал функции одной
переменной».
Студентам предлагается домашняя работа, содержащая
теоретическую и практическую части, призванная подготовить их к изучению темы
во время семинарских занятий.
Теоретическая часть включает в себя
следующие задания:
1) дать определение производной;
2) выучить таблицу производных;
3) сформулировать геометрическое, механическое и
экономическое значение производной;
4) сформулировать теорему о производной сложной функции;
5) дать определение дифференциала функции;
6) записать формулу углового коэффициента касательной к
кривой в заданной точке;
7) дать понятия левой и правой производной функции в
заданной точке;
8) составить алгоритм приближенного вычисления значения
функции.
Заданный теоретический материал студенты
могут подготовить с помощью прочитанных преподавателем лекций, но целесообразно
указывать также использованную дополнительную литературу [3,4].
Кроме того, в данную работу необходимо включать
демонстрационные и аналогичные им примеры.
Пример
1. Вычислить производную функции ![]()
Решение: ![]()
Решить аналогичную задачу: Вычислить производную
функции ![]()
Пример
2. Вычислить дифференциал функции ![]() в точке
в точке ![]() Дифференциал равен
Дифференциал равен ![]() По таблице
производных элементарных функций получаем:
По таблице
производных элементарных функций получаем:
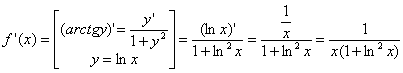
![]()
![]()
Решить аналогичную задачу: вычислить
дифференциал функции ![]() в точке
в точке ![]()
Пример
3. Найти левую ![]() и правую
и правую ![]() производные функции
производные функции ![]() в точке
в точке ![]()
Так как функция ![]() дифференцируема в
окрестности точки
дифференцируема в
окрестности точки ![]() то
то ![]() Аналогично для
функции
Аналогично для
функции ![]() Но при
Но при ![]() (слева)
(слева) ![]() а при
а при ![]() (справа)
(справа) ![]() В итоге имеем
В итоге имеем ![]() и
и ![]()
Решить аналогичную задачу: найти левую ![]() и правую
и правую ![]() производные функции
производные функции ![]() в точке
в точке ![]()
Пример
4. С помощью дифференциала первого
порядка вычислить приближенно ![]() .
.
Воспользуемся формулой ![]() Положим,
Положим,![]() тогда получаем
тогда получаем ![]() так как
так как ![]() получаем, что
получаем, что ![]()
Решить аналогичную задачу: с помощью
дифференциала первого порядка вычислить приближенно ![]()
Такие домашние работы студенты могут выполнять
в группах. В таком случае работу оценивает консультант. Однако подобные задания
могут быть предложены и как самостоятельная домашняя работа, проверяемая
преподавателем с последующим обсуждением на семинарском занятии и анализом
типичных ошибок.
На занятии целесообразно решать задачи
двух уровней сложности.
Задачи
I уровня:
1.Найти угловой коэффициент касательной к
кривой ![]() в точке с абсциссой
в точке с абсциссой ![]()
2.Чему равна производная в точке ![]() функции
функции ![]() , обратной к функции
, обратной к функции ![]() если
если ![]()
3. Вычислить производную функции 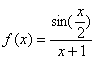 в точке
в точке ![]()
4. Вычислить дифференциал функции ![]() в точке
в точке ![]()
5. Чему равна производная в точке ![]() функции
функции ![]() обратной к функции
обратной к функции ![]() если
если ![]()
Задачи
II уровня:
1.
Найти левую ![]() производную функцию
производную функцию ![]() в точке
в точке ![]()
2.
Найти правую ![]() производную функции
производную функции ![]() в точке
в точке ![]()
3.
Вычислить приближенно ![]() .
.
4.
Вычислить приближенно ![]()
Итогом работы должна быть проверочная
самостоятельная работа, составленная из заданий, аналогичных решенным на
семинарском занятии.
Использованные
источники
1. Тишков К.Н., Кошелев О.С., Мерзляков И.Н. Роль и методы самостоятельной работы студентов в современных условиях. Н/Новгород: НГТУ, 2008 .
2. Гусак А.А. Математический анализ и дифференциальные уравнения, справочное пособие. Мн.: ТетраСистемс, 2006.
3. Красс М.С., Чупринов В.В. Математика для экономистов. М.; СПб, 2010.
4. Л.Г. Корсокова. Высшая математика для менеджеров: учеб. пособие. Калининград: Калининград. унт, 1997.