Современные методы преподавания

Konyrbayeva N.N.

Uralsk, M. Utemisov WKSU, 2 year undergraduate

Kulzhumieva A.A.

Uralsk, M. Utemisov WKSU, Physics and Mathematics department head, candidate of physical and mathematical sciences

FORMATION OF STUDENTS' SPATIAL THINKING WITHIN ACTIVITY APPROACH

The system and activity approach is a cornerstone of new generation education standards. The purpose of this approach is a development of personality [1]. Participation of a child in educational process as the doctrine subject is a cornerstone of activity approach technology. The basic principle of activity approach is that knowledge is not presented in ready form; students receive information participating in research activity independently. That is this standard helps to teach to study as knowledge is exactly generated in a process.

The concept of system and activity approach was introduced in 1985 as a special type of concept. Even at that time scientists tried to remove contradictions in psychological science between system approach which was developed in researches of classics (such as B.G. Ananyev, B.F. Lomov and a number of researchers), and activity which was always a system (it was developed by L.S. Vygotsky, L.V. Zankov, A.R. Luriya, D.B. Elkonin, V.V. Davydov and many other researchers). System and activity approach is an attempt of these approaches association.

The concept of system and activity approach specifies that the result can be reached only if there is a feedback.

System and activity approach provides:

- formation of readiness for self-development and continuous education;

- design and designing of social environment of the students' development in an education system;

- students' activity in educational cognitive activity;

- creation of educational process taking into account specific age, psychological and physiological features of students.

This approach in training is aimed at the development of each student, at the formation of their individual abilities, and also allows to strengthen knowledge considerably and to increase the rate of material studying without students' overload. The technology of activity method of training does not destroy "traditional" system of activity, and transforms it, keeping all necessary for the realization of new educational objectives.

System and activity approach in teaching Mathematics demands formation of practical abilities of the theory application. The position of Mathematics teacher has to be is as follows: not with an answer for the class, but with a question. Students have to be able to allocate, compare, generalize, estimate mathematical concepts at the lesson, to create mathematical models, i.e. to own those universal ways which will be useful to them in practice.

As V.A. Dalinger noted, the base for practical activities on many specialties is an orientation of a person in space [2]. Development of spatial thinking of school students has a special importance.

Spatial thinking is quite difficult many-sided and multilevel mental process which takes place in the solution of tasks demanding orientation in practical and theoretical space (both visible and imagined).

A large number of works of teachers, psychologists and mathematicians such as I.S. Yakimanskaya, G.D. Glazer, I.Ya. Kaplunovich, V.A. Dalinger, E.N. Kabanova-Meller, A.D. Botvinnikov, G.I. Sarantsev and V.A. Krutetsky who considered this question in various aspects [3-6], is devoted to the problem of development of school students' spatial thinking.

However, practice of Mathematics training establishes the fact of weak spatial representations existence and insufficiently developed spatial thinking of students.

As a rule, complaint about weak spatial thinking of students begins in the tenth grade. It is explained by transition from planimetry to systematic studying of stereometry course and, in this regard, sharp increase of complexity in operating not by two-dimensional, but three-dimensional objects. And such situation of teachers strongly excites and all the time pushes each of them on new searches. We are not talking about stereometric knowledge of students and inability to solve their complex problems, and about their geometrical thinking and geometrical representations as development of geometrical thinking and spatial representations of students is the most important problem of Geometry lessons and Mathematics teacher first of all.

How to organize the process of training for receiving maximum results in assimilation of knowledge by students, skills development, cogitative activity, spatial thinking in particular?

Developed spatial thinking is an indicator of the child's developed imagination. As far as child imagining figures in mind can carry out various operations over this figure. The question is: How to develop a child's imagination? Development of imagination is a purposeful process pursuing tasks to develop brightness of the imagined figures, their originality and depth, and also fruitfulness of imagination.

A person is not born with the developed imagination. Development of imagination is carried out during ontogenesis of a person and demands accumulation of a known stock of representations which can serve further as a material for creation of imagination figures. Imagination is developed in close connection with the development of the whole personality, in the course of training and education, and also in unity with thinking, memory, will and feelings [7].

All mental processes including spatial imagination are improved as a result of activity. This activity has to be stimulated and directed, i.e. the system of exercises is necessary.

For the solution of many of these tasks special knowledge is not needed, i.e. they can be offered already in the V grade, and some — and at elementary school.

1. Divide round sausage with three cuts into 8 parts. [Answer in fig. 1].

2. Put four correct triangles out of six matches so that the whole match will be the party of each of them. [Triangular pyramid with edge a equal to a match].

3. Arrange 5 identical coins so that each of them will touch four others. [Answer in fig. 2].

4. Is it possible to arrange 6 identical pencils so that each of them will touch five others? [It is possible, the answer in fig. 3].

fig. 1 fig. 2 fig. 3

5. In fig. 4a the bald line showed the figures bent from a wire. Represent three of their projections: on a forward side of a cube, on its lateral edge and on the upper edge. [Answers in fig. 4b are under the images of the corresponding figures].

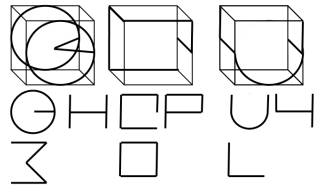
a

b

fig. 4

However in all cases, models are desirable to do after the decision, but not for the decision. If a teacher begins consideration of the offered tasks with models, the students' imagination is not involved and incentive for its development turns out weak.

In summary we will note that originality of tasks causes interest in students both during the work at the lesson and in out-of-class activity, and it is one of necessary conditions of subject successful studying.

References:

1. State educational obligatory standard of the Republic of Kazakhstan, 12-year secondary general education. Astana. 2006.

2. V.A. Dalinger, Technique of students' spatial representations formation at Geometry lessons. – Omsk: OGPI, 2005.

3. I.S. Yakimanskaya, Psychological bases of mathematical education: manual. – M.: Publishing center "Akademiya", 2004.

4. G.D. Gleizer, Methods of formation and development of spatial representations of school students at Geometry lessons. - M.:1984.

5. I.Ya. Kaplunovich, Psychological regularities of spatial thinking development // Psychology issues. - 1999. - №1. - P. 64-68.

6. E.N. Kabanova-Meller, Educational activity and evolutive training. – M.: Education, 1981.

7. A.G. Maklakov, General psychology. SPb: Piter, 2001.