Яловенко С.Н.
Рассматривается
природа физических явлений – теория гравитации, гравитация черной дыры, гравитационное взаимодействие, электрический
заряд.
Ключевые
слова: гравитация, чёрная дыра, гравитационное взаимодействие, физика эфира,
закон Кулона, заряд.
Author Yalovenko S. N. Black limit. Part
14.4.
We consider the nature of physical phenomena -
the theory of gravity, the gravity of the black hole, the gravitational
interaction, electric charge.
Keywords: gravity, black hole, the
gravitational interaction, physics, ether, Coulomb's law, charge.
Чёрный предел. Часть 14.Глава 4.
Природа физических явлений.
Гравитация как сумма плоских водоворотов.
В предыдущих работах проводились
исследования по гравитации. В результате эфирного парадокса было установлено,
что гравитация, которая обратно пропорциональна квадратам расстояния (1), есть
приближёние некоторой более полной формулы описывающую эту гравитацию(2,3).
Fгравитации(r) =GMm× [1/r2] (1)
Fгравитации(r) =GMm× [1/(Δr2+r2)] (2)
Fгравитации(r) =GMm× [1/(Δr2+(f(r)+r)2)] (3)
Была выдвинута гипотеза, что возможно эта
функция есть нормальным процессом.
Fгравитации(r) =GMm×[[1/(Δr)2] × ехр(-G1×r2)] (4)
Гипотеза была выдвинута на основании
водоворотной теории из утверждения, что если на тело действует множество
равнозначных по величине сил, то поведение этого тела будет описываться
нормальной функцией.
Из проведенных экспериментов и моделирований
оказалось, что это не соответствует выдвинутой гипотезе (рис.1).
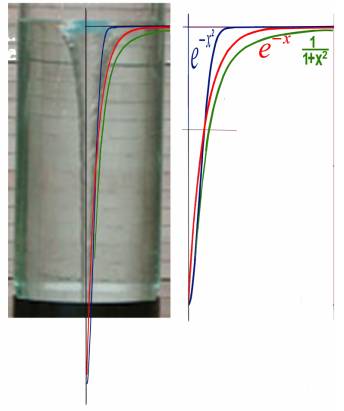

Рис.1.Моделирования водоворота.
Поведение водоворотов ближе описывается
экспоненциальной функцией Aехр(-r/σ) (Ae-r/σ
), что потребовало отказаться от ранее
выдвинутой гипотезы. Возможно для световых процессов экспонента
ближе по своей природе. Так экспонентой описывается радиоактивный распад
вещества, а так же ранее выводимый процесс стирания света при прохождении его через эфир, отвечающий за красное смещение
спектра звезд, в зависимости от расстояния (рис.2.), ошибочно принимающиеся за
расширение и расширение с ускорением звездных масс (галактик, вселенной).
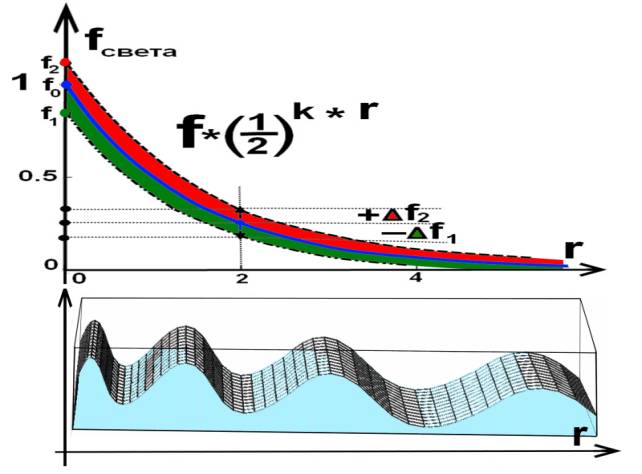
Рис.2.Модель потери энергии света при прохождении
через эфир.
С учетом вышесказанного формулу (3) можно записать
как:
Fгравитации(r) = GMm×[1/(Δr2+r2)] × f1(r) (5)
Где f1(r) –весовая функция,
отражающая экспоненциальныё процессы при формировании гравитации.
Формула (3) и (5) равны и представляют
собой разные формы записи одной и той же функции, формула (3) - через
искривление пространства, формула (5) - через весовую функцию.
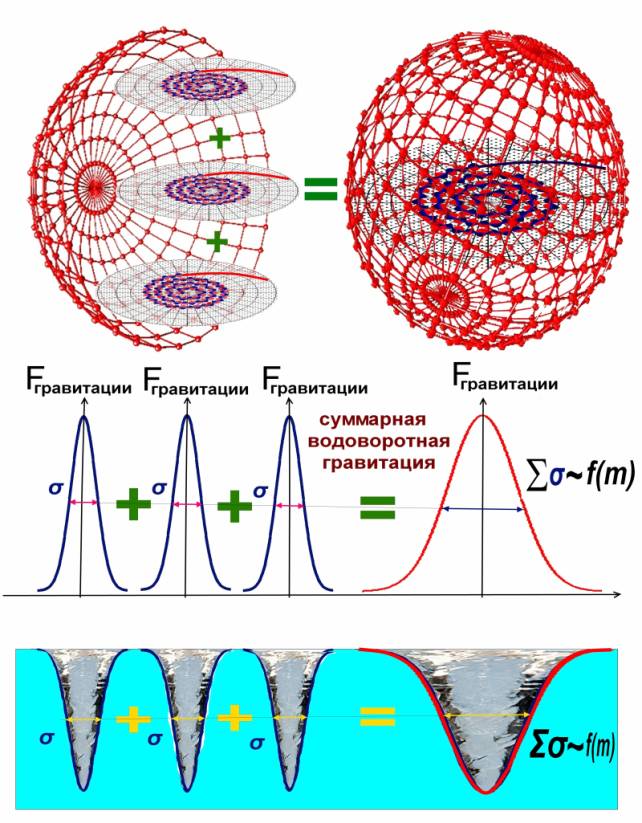
Рис.3. Суммирование дисперсий σ водоворотов.
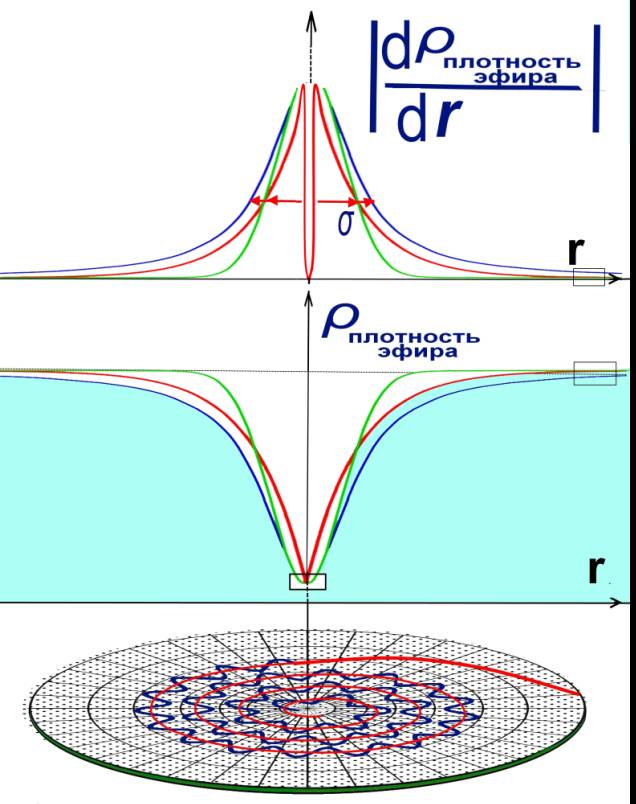
Рис.4.Изменение плотности эфира и гравитации в
водовороте элементарной частицы..
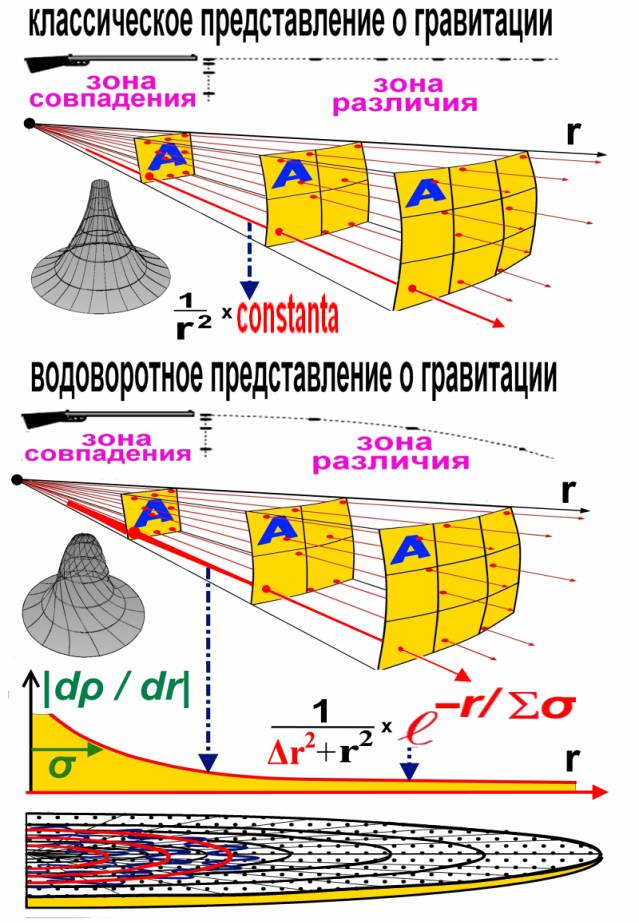
Рис.5. Модель гравитации представленной суммой плоских водоворотов.
Изначально в эфирной теории гравитация
была представлена суммой гравитаций плоских, статистически равномерно
вращающихся эфирных водоворотов (6),(7).
Fгравитации(r)=P(λ,β) fводоворота(Σ ρ плотность эфира протонов(r)) (6)
Где P(λ,β) =1/r2 – ‘это
не гравитация, а статистическое распределение суммарной эфирной плотности
гравитационных центров эфирных водоворотов (протонов).
Где P(λ,β) – вероятностная функция распределения по углам λ и β, ρплотность
эфира протонов(r) – эфирная
плотность распределения протона в пространстве, Σ ρ плотность эфира протонов(r) – суммарная эфирная плотность распределения протонов
в пространстве, fводоворота(Σ
ρ плотность эфира протонов(r)) - функция суммарной гравитации от протонных водоворотов,
зависящая от сформированного ими суммарного градиента (дифференциала,
приращения) плотности эфира.
Гравитация протонного водоворота
представлялась как:
![]() (7)
(7)
где fводоворота(Σ
ρ плотность эфира протонов(r))- гравитационная функция от суммарной плотности,
создаваемая водоворотами.
Процесс формирования суммарной плотности
от плоских протонных водоворотов показан на рис.3,4,5. Полученная из модельных
экспериментов формула распределения плотности эфира для протона равна:
ρ плотность эфира протона (r)=ρ + (r) =ρ0×(1- e-r/σ) (8)
Производная от формулы (8) или гравитация,
создаваемая одним протонным водоворотом равна:
|∂ρ
плотность эфира протонов /∂r|=
=|∂ρ
+ /∂r|= ρ0×1/σ× e-r/σ=(m0/σ) ×e-r/σ (9)
Где m0 – масса протона, ρ0 – начально
создаваемая водоворотом эфирная плотность протона, σ – дисперсия
водоворота.
Вычислим суммарную гравитацию создаваемую водоворотами: fводоворота(Σ ρ плотность
эфира протонов(r))=|∂ρ
+ /∂r|=
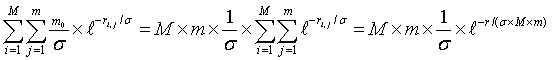 (10)
(10)
Получим, что гравитация суммарного протонного водоворота
равна:
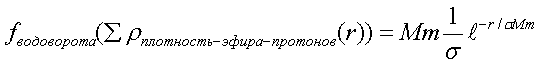 (11)
(11)
Подставим значение формулы (11) в формулу (6), получим:
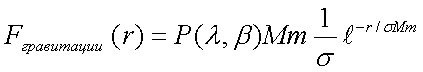 (12)
(12)
Где P(λ,β)=1/r2, подставим
её в формулу (12) и получим:
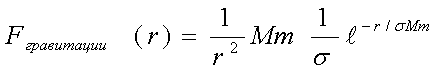 (13)
(13)
Сравнивая с классической формулой гравитации
Fгравитации(r) =GMm× [1/r2]
видим, что
G=1/σ
гравитационная постоянная обратно
пропорциональна дисперсии (G=6,6·10−11 м3·с−2·кг−1)
тогда с учетом согласования размерности для суммы водоворотов в одном килограммометре
дисперсия равна:
σ=0.15×1011 м3·с−2·кг−1.
Исходя из этого, суммарная расширенная формула
для гравитации, совмещенная по размерности, будет равна:
Fгравитации(r) =GMm×[1/r2]×e-r/σMm (14)
Так как величина e-r/σMm≈1 на соизмеримых расстояниях при r<<σMm то расширенная
формула для гравитации (14) примет классический вид с достаточно хорошей
степенью приближения:
Fгравитации(r) ≈GMm×[1/r2]
Как видно классическая формула гравитации
(1) является приближением от расширенной формулы гравитации (14).
Самая близкая механическая модель
гравитации это стрельба из ружья, приводимая в предыдущих работах. В зоне, где
скорость пули можно считать приближенно постоянной (Vпули=COVSTANT) давления на стены мишени пропорциональны квадрату
расстояния (1/r2, как показано на рис.5), в нашем случае это зона до
Плутона. Но на более длительные расстояния надо учитывать потерю энергии пули.
Для этого необходимо умножать 1/r2 на exp(-r/K×Wэнергия).
Где Wэнергия –
энергия пули (в нашем случае на e-r/Σσ – на коэффициент изменения суммарной плотности эфира), σ – коэффициент,
определяющий скорость изменения величины e-r/σ
и называется постоянной экспоненты
(рис.6), аналог среднеквадратического
отклонения для нормального закона распределения, и по аналогии можно называть
дисперсией.
В степенной функции работает принцип
половина от половины или если вы потеряли половину энергии при прохождении расстояния
r, то на следующем интервале r вы
потеряете половину от половины энергии. Вы как бы выстреливаете с половины пути
r половинной
энергией.
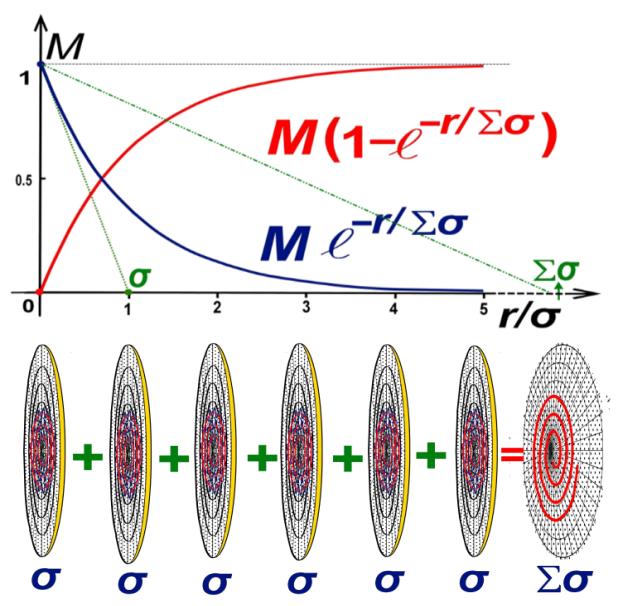
Рис.6. Сложение дисперсий водоворотов при формировании
суммарной изменяющейся плотности эфира.
Все выше изложенные взгляды на гравитацию отображали
собой изначальное эфирное представление о гравитации, как об изменяющейся
плотности эфира, упрощёно и в доступной форме показанной на рис.7.
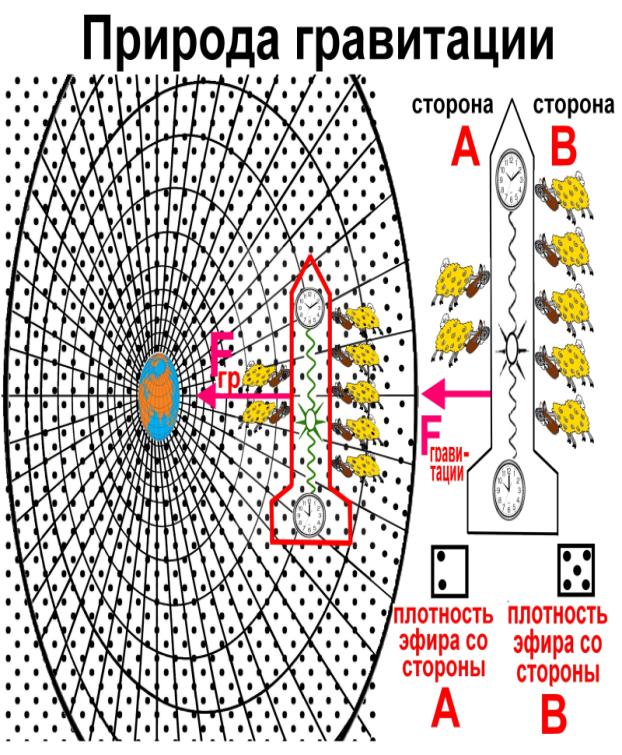
Рис.7
При более тщательном
моделировании оказалось, что при приближении к нулю экспоненциальная функция
имеет вид изображенный на рис.8,9,10. Такое поведение напоминает матрёшку когда
при приближении к пределу включаются новые законы, не известные ранее.
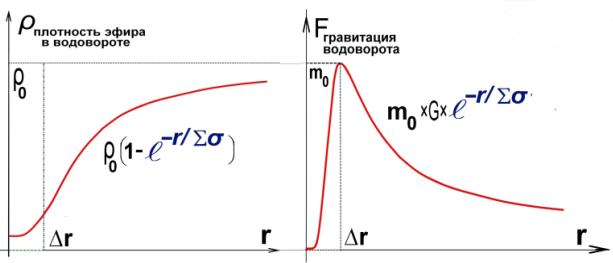
Рис.8. Графики изменения плотности эфира и гравитации.
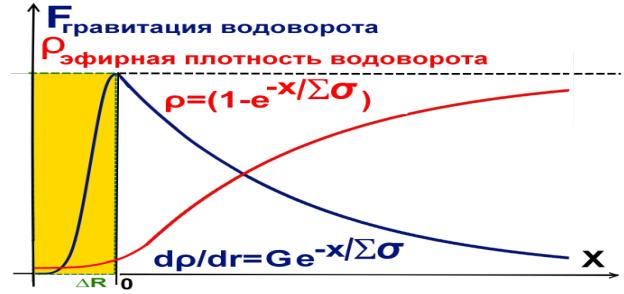
Рис.9. Графики изменения плотности эфира и гравитации.
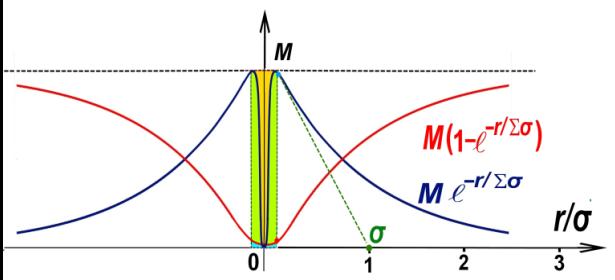
Рис.10. Графики изменения плотности эфира и
гравитации.
Всякая новая теория должна обладать
предсказательной силою. Так таблица Менделеева предсказала новые элементы. В
данной водоворотной эфирной теории, где P(λ,β)=[1/(Δr2+r2)]≈1/r2 – функция статистического распределения давления эфира,
аналог распределения давления пуль при стрельбе из ружья, Δr – это расстояние или предел до которого
можно сжать тело. Этот предельный радиус равняется световому радиусу звезды.
Предсказывается, что при приближении к предельному радиусу гравитация от
сферической формы перейдет к плоской форме (приближённо эллипсоидной) (рис.11,12).
То есть при приближении r→ 0
P(λ,β)=[1/(Δr2+r2)]≈1/Δr2 (15)
плоскости водоворотов не смогут совершать
статистически равномерное вращение под действием эфирных флуктуаций и начнут
мешать друг другу, в результате чего, вероятностная функция статистического
распределения примет вид:
P(λ,β)=e-λ/σ (16)
Как следствие этого, гравитация от сферической
формы перейдёт в плоскую форму (рис.11,12). Так произведя нормировку суммарной
гравитации (14) на угловой интервал [от 0…π] расширенная нормированная формула
гравитации (14) при r≈ Δr запишется как:
Fгравитации(r) =GMm ×e-(r–π)/Σσ ×e-r/Σσ (17)
Где [1/(r∑σ)2]
=e-(r–π)/Σσ ×e-r/Σσ = const
где GMm=К≈const –
постоянная величина,. Тогда формулу (17) гравитации для нормированного интервала
[от 0…π] можно записать в виде:
Fгравитации(r) =К×e-(r–π)/Σσ ×e-r/Σσ=Constant (18)
Формула гравитации (18) показана на
рис.11., где видно, что форма гравитации перешла от сферической к плоской
форме, то есть гравитация чёрной дыры плоская как показано на рис.12.
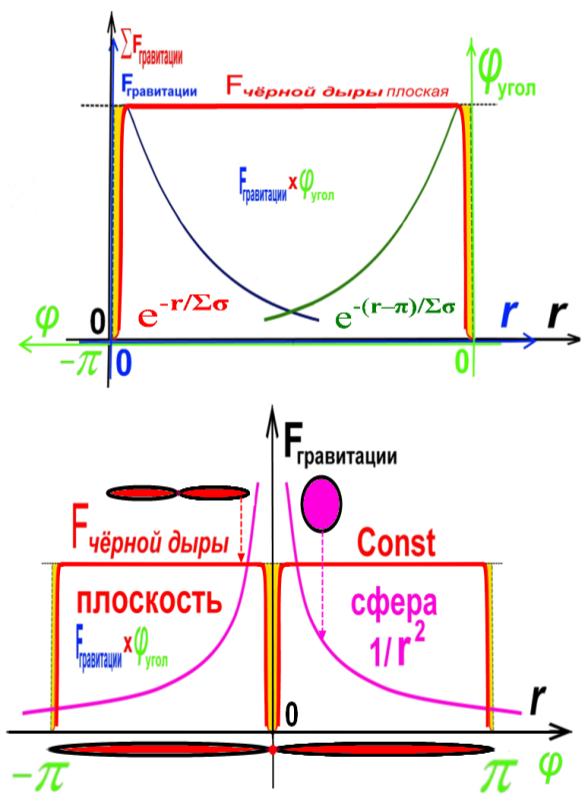
Рис.11.Нормированные графики формирования плоской
гравитации для чёрной дыры.
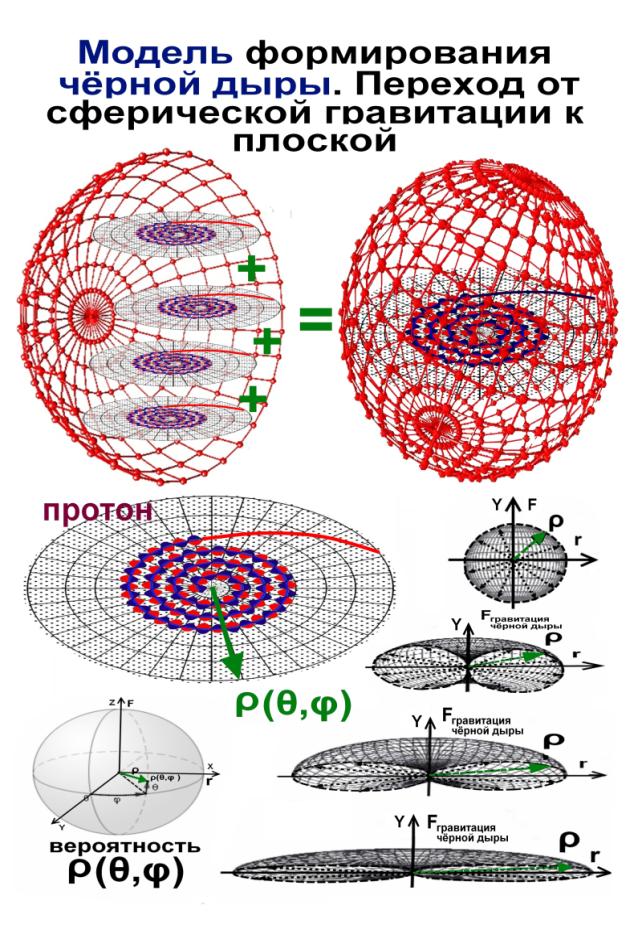
Рис.12.Переход от сферической гравитации к плоской
гравитации.
Логику рассуждений можно свести к следующему:
1)Свет - это поступательное движение.
2)Частица - это вращательное движение, при котором
создаётся стабильное изменение плотности эфира.
3)Изменение плотности эфира создает гравитационную
силу – гравитацию (Fгравитации водоворота(r) = d ρплотность
эфира ( r)/dr и F![]() (r) = d ρ
(r) = d ρ![]() ( r)/dr)
( r)/dr)
Для описания электромагнитных явлений используется та
же плоская водоворотная модель. Электрон это свёрнутая правильным водоворотом
электромагнитная волна. Заряд электрона это растянутая водоворотом последняя не
свёрнутая полуволна как показано на рис.13,14,15.
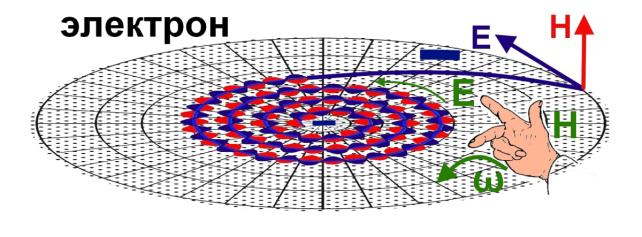
Рис.13. Модель электрона.
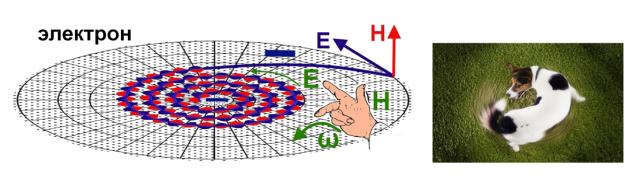
Рис.14. Модель электрона.
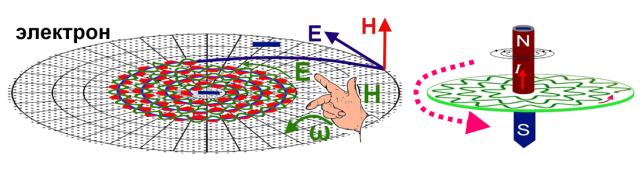
Рис.15. Модель электрона.
Гравитация и электромагнитные явления
описываются одной моделью, с одной позиции, одним физическим процессом.
Механическая модель взаимодействия электронов
в проводнике изображена на рис.16,17. Для описания взаимодействия электронов используется
правило правой руки.
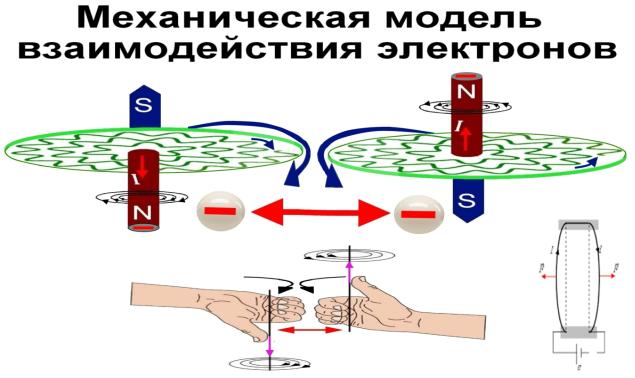
Рис.16. Механическая модель взаимодействия электронов
по правилу правой руки.
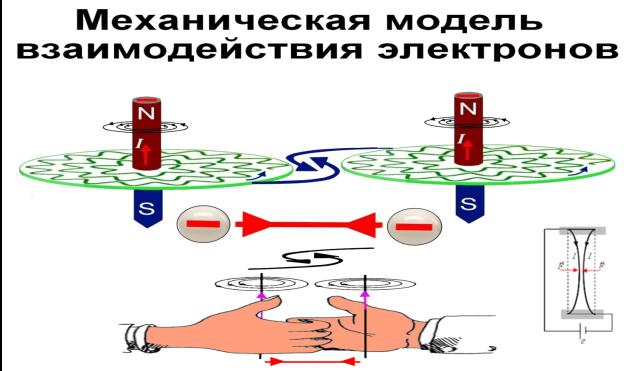
Рис.17. Механическая модель взаимодействия электронов
по правилу правой руки.
Что бы электроны притягивались их нужно
пустить по силовым линям проводников (по проводам) и отталкивание сменяется
притяжением проводников рис.17.
Свободный электрон это сфера с внешним
электрическим зарядом сформированным из-за статистически равновероятностного (равномерного)
вращения и колебания вокруг своей оси плоского водоворота – аналог броуновского
движения частицы в жидкости. Механический аналог это статистически равномерно
вращающийся вокруг своей оси вентилятор. Расширенный закон Кулона, который
выводился ранее, отражает эту особенность (где напряженность поля
электромагнитной волны E0=q1, E0=q2):
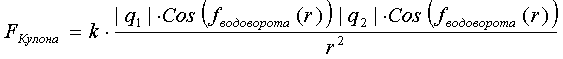
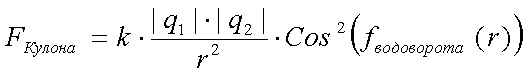
при r << Σσ
тогда Cos (fводоворота)≈1 и
формула Кулона примет классический вид:
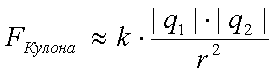
В проводнике движение электрона
упорядочивается силовыми линиями внутри проводника, и взаимодействие
определяется направленностью движения заряда (электронов, протонов и т.д.)
рис.16,17.
Подход плоских эфирных водоворотов позволяет описывать
множество физических процессов, с единой позиции, не прибегая к многомерным
пространственным теориям, в рамках классической физики. А также делать процессы
зримыми, наглядными, упрощая их понимание.
Список
используемой литературы:
1.
А. Эйнштейн, Теория относительности [Текст] / А. Эйнштейн. – Научно-издательский центр
"Регулярная и хаотическая динамика", 2000.
2.
Ацюковский, В. А. Общая
эфиродинамика. Моделирование структур вещества и полей на основе представлений
о газоподобном эфире [Текст] / В. А. Ацюковский. – М.:
Энергоатомиздат, 1990.
3.
Яловенко, С. Н. Чёрный предел. Теория относительности: новый взгляд [Текст] / С. Н. Яловенко. – ТОВ издательство «Форт», 2009. ISBN 978-966-8599-51-4
4.
Яловенко, С. Н. Фундаментальная
физика ... LAP LAMBERT Academic
Publishing (06.08.2013 ) 180 страниц, Pubblicato il: 06.08.2013 ISBN: 978-3-659-43971-1
5.
Яловенко, С. Н. Эфирная теория относительности. Гравитация.
Заряд.[Текст] / С. Н. Яловенко-
Харьков. Издательство «ЛИДЕР», 2015г. -268 страниц. ISBN 978-966-2732-31-3
Научное издание