ОБ ОДНОЙ ОЦЕНКЕ ДАВЛЕНИЯ И ОБЪЁМНЫХ МОДУЛЕЙ
В РАСПЛАВЛЕННЫХ СИСТЕМАХ
Севастьянов Максим
Михайлович
Расплавленные металлы и их сплавы находят
широкое применение в народном хозяйстве. Этот интерес особенно велик в
теплотехнике, ядерной и электронной технике и других отраслях промышленности, а
также для удовлетворения потребностей металлургического производства и в
разработке новых технологий в этой
области. Наибольшее внимание расплавленным металлам уделено в металлургии, что
обусловлено необходимостью прохода жидкой фазы перед кристаллизацией.
Практическая значимость ожидаемых результатов работы заключается в возможности
использования новых представлений о строении расплавов, основанных на
компьютерном моделировании, позволяющем моделировать свойства расплава на
атомном уровне, что важно для выработки оптимальных технологических процессов в
цветной и черной металлургии, в пирометаллургии в целом, происходящих на
поверхности раздела фаз, а также для аналогичных процессов в технологии
неорганических материалов (кремния, селена, теллура, германия и т.п.), в том
числе и для нанопокрытий, пленок и других специальных технологий.
Для расчёта объёмных модулей в расплавленных
системах необходимо рассмотреть некоторые соотношения. Расплавы металлов и полупроводников можно
рассматривать как двухкомпонентную жидкость, состоящую из ионов и электронов,
тогда по теореме вириала может быть оценена часть давления, связанная с
динамикой и взаимодействием ионной подсистемы, т. е.
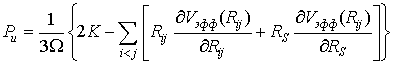 , (1)
, (1)
где K –
кинетическая энергия.
Для
расчета полного давления к величине Рион
необходимо добавить давление, созданное ферми-газом, равное сумме
производных энергий Е0(Ω)
и Ер
(Ω) с обратным знаком ![]() .
Давление Рион можно
переписать в интегральной форме, содержащей в явном виде зависимость от
структуры g(R). Если кинетическую
энергию выразить через температуру, то
.
Давление Рион можно
переписать в интегральной форме, содержащей в явном виде зависимость от
структуры g(R). Если кинетическую
энергию выразить через температуру, то
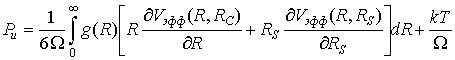 (2)
(2)
Производная 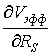 в выражении для давления специфична для
расплавов, поскольку Vэфф(R, Rs) является не только функцией
расстояния, но и функцией Ω = Ω(Rs). Это указывает на то, что результат
является следствием зависимости диэлектрической функции проницаемости, которая
характеризует косвенное взаимодействие ионов от плотности экранирующей
электронной подсистемы nz,
при этом
в выражении для давления специфична для
расплавов, поскольку Vэфф(R, Rs) является не только функцией
расстояния, но и функцией Ω = Ω(Rs). Это указывает на то, что результат
является следствием зависимости диэлектрической функции проницаемости, которая
характеризует косвенное взаимодействие ионов от плотности экранирующей
электронной подсистемы nz,
при этом ![]() .
Проведенный расчет для Na показывает,
что члены Рион и
.
Проведенный расчет для Na показывает,
что члены Рион и ![]() , которые входят в давление РЭГ, дают близкие к нулю значения, в то время как
добавка от кинетической энергии, умноженная на Ω, составляет 0,003
Рдб/ион. Поскольку объемный модуль, как будет показано далее, составляет
примерно 0,1 Рдб/ион, то достижение равновесия требует изменения Rs
примерно на 1 %, и
это является довольно хорошим
результатом. Кроме того, необходимо учесть сделанные приближения, в частности,
некоторую неопределенность члена, связанного со сжимаемостью, который дает
около 10 % от общего вклада.
, которые входят в давление РЭГ, дают близкие к нулю значения, в то время как
добавка от кинетической энергии, умноженная на Ω, составляет 0,003
Рдб/ион. Поскольку объемный модуль, как будет показано далее, составляет
примерно 0,1 Рдб/ион, то достижение равновесия требует изменения Rs
примерно на 1 %, и
это является довольно хорошим
результатом. Кроме того, необходимо учесть сделанные приближения, в частности,
некоторую неопределенность члена, связанного со сжимаемостью, который дает
около 10 % от общего вклада.
Если при оценке давления пренебрегают изменением
парного потенциала Vэфф(R) от
плотности, то результат оказывается завышенным. Отсюда следует, что в моделях с
жестко фиксированной плотностью, воспроизводящих N, Q,, Т ансамбль, приходится иметь дело с большими положительными
давлениями. Такая ситуация наблюдается при расчете силовых постоянных в
кристалле. Указанный вывод не говорит о некорректности упомянутых моделей для
жидкого металла. Равновесные состояния необходимо рассматривать одновременно
для обеих его подсистем – ионной и электронной, поскольку положительное
давление ионной подсистемы определяет объемные эффекты в электронной
подсистеме.
Как известно, в теории конденсированных систем
существует «правило сумм сжимаемости», которое характеризует, насколько
построенная модель системы является самосогласованной. Обратная величина
объемного модуля равна упомянутой сжимаемости. Эти величины важны при
рассмотрении свойств конденсированных систем. В кристалле статический объемный
модуль βст, равный
второй производной энергии по объему, должен согласовываться с динамическим
объемным модулем βдин , являющимся
комбинацией постоянных упругости, рассчитываемых по соотношению дисперсии фононов
методом «длинных» волн.
Указанное соотношение определяется межатомным
взаимодействием при постоянном объеме и не зависит от объемно-зависящих членов
энергии. В этой самосогласованной модели соотношение между формой эффективного
взаимодействия при Q=const и производными энергии по объему, содержащей
упомянутые члены, и определяет «правило сумм сжимаемости».
Это дает основание утверждать, что появляющиеся в
динамической матрице в третьем и четвертом порядках члены в длинноволновом
пределе дают вклад второго порядка. Это несоответствие проистекает из-за
включения этих вкладов при расчете статических модулей и пренебрежения их в
динамических модулях. Но включение этих высших членов при построении
динамической матрицы, соответствующих триплетному и квадрупольному взаимодействию,
принципиально возможно. Проведенные расчеты с кристаллическим Na показали, что для приведения к
согласию рассчитываемого статического модуля βст экспериментальному необходимо варьировать
энергию Хартри. Но при такой вариации хорошо согласовывавшийся с экспериментом
динамический модуль βдин
оказывается слишком завышенным.
Возможное объяснение этого состоит в том, что члены
третьего и четвертого порядков становятся более важными в динамической матрице
в области при малых q. В данном случае для
сохранения согласия с экспериментом необходима модификация самого
псевдопотенциала в этой указанной области. В таком случае вариация энергии
Хартри будет соответствовать этому модифицированному псевдопотенциалу.
Статический изотермический модуль упругости жидкой
фазы является следующей производной давления по объему:
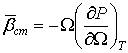 .
(3)
.
(3)
Динамический изотермический модуль определяется
длинноволновым пределом структурного фактора S(q):
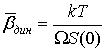 . (4)
. (4)
Оба этих модуля в согласованной теории должны
совпадать. Однако применение теории возмущения во втором порядке по
псевдопотенциалу и определение динамического модуля через S(q) в
модели с не зависящим от плотности потенциалом приведет к расхождениям, как и в
случае кристалла. Точное выражение для статического модуля можно записать как:
![]()
![]() ,
(5)
,
(5)
где
![]() ,
,
где D –
оператор, введенный для сокращения записи:
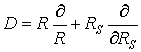 .
.
Физически смысл производных остается прежним, как и
в случае уравнения (2). Подытоживая, можно записать:
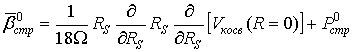 , (6)
, (6)
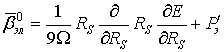 . (7)
. (7)
Аналогичное выражение можно записать для
динамического модуля ![]() , поскольку он
также рассчитывается в модели с не зависящим от плотности потенциалом.
Поскольку модель является самосогласованной, то рассчитываемые в ней
динамический и статический модули совпадают. Аналогичный вывод можно сделать и
в случае расчета сжимаемости кристалла, выполненного в обратном пространстве.
Таким образом, требуется, чтобы выполнялось следующее соотношение:
, поскольку он
также рассчитывается в модели с не зависящим от плотности потенциалом.
Поскольку модель является самосогласованной, то рассчитываемые в ней
динамический и статический модули совпадают. Аналогичный вывод можно сделать и
в случае расчета сжимаемости кристалла, выполненного в обратном пространстве.
Таким образом, требуется, чтобы выполнялось следующее соотношение:
![]() , (8)
, (8)
где
![]() .
.
Уравнение (4) дает более простое выражение для ![]() . Эквивалентность уравнений (4) и (6) является по существу
частным случаем условий согласования между
n и n+1 частичными функциями распределения. Уравнение (8) не содержит
указания к расчету статической сжимаемости (5). Однако при вычислениях по
уравнению (5) приходится сталкиваться со следующими проблемами:
. Эквивалентность уравнений (4) и (6) является по существу
частным случаем условий согласования между
n и n+1 частичными функциями распределения. Уравнение (8) не содержит
указания к расчету статической сжимаемости (5). Однако при вычислениях по
уравнению (5) приходится сталкиваться со следующими проблемами:
а) для расчета требуется такая функция радиального
распределения g(R), которая была бы
согласована с полной теорией, т.е. чтобы выполнялось тождество:
![]() ,
(9)
,
(9)
равное kT/Ω![]() . Это требует включения в рассмотрение членов третьего и
четвертого порядков в области малых q. Так как эти члены
соответствуют расчету эффективных взаимодействий между тремя и четырьмя ионами,
то это трудно выполнимо. Естественно поэтому сделать предположение, что функция
g(R), рассчитанная в компьютерном
эксперименте с парным эффективным потенциалом при Ω =
const, не приводит к большим ошибкам, исключая длинноволновую область. Именно
эта функция g(R) и подставляется в
уравнение (5) и (8);
. Это требует включения в рассмотрение членов третьего и
четвертого порядков в области малых q. Так как эти члены
соответствуют расчету эффективных взаимодействий между тремя и четырьмя ионами,
то это трудно выполнимо. Естественно поэтому сделать предположение, что функция
g(R), рассчитанная в компьютерном
эксперименте с парным эффективным потенциалом при Ω =
const, не приводит к большим ошибкам, исключая длинноволновую область. Именно
эта функция g(R) и подставляется в
уравнение (5) и (8);
б) уравнения (5) и (8) требуют значения производных
функций g(R) по объему, которые могут
быть получены повторением компьютерного эксперимента с различными исходными
плотностями.
Данное положение представляет собой крайне
трудоемкую задачу. Поэтому более удобно ограничиться приближением:
![]() , (10)
, (10)
где f(R/RS ,T) – функция,
которая обеспечивает одинаковое изменение структуры с плотностью при неизменной
температуре.
Однако предположение (10) справедливо для
кристаллической структуры, но не обязательно выполняется для жидкости. Поэтому
из этого приближения непосредственно следует, что:
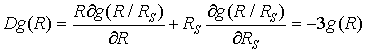 (11)
(11)
С учетом полученного результата уравнение (4)
перепишем следующим образом:
![]() (12)
(12)
Значение для ![]() 0,097, найденное без вариации энергии Хартри,
согласуется с экспериментальным, равным 0,0973, как и в случае кристалла.
Значение S(0), установленное машинным
экспериментом, составляет 0,032±0,002, что приводит к
0,097, найденное без вариации энергии Хартри,
согласуется с экспериментальным, равным 0,0973, как и в случае кристалла.
Значение S(0), установленное машинным
экспериментом, составляет 0,032±0,002, что приводит к ![]() Ω
= 0,078±0,005.
Ω
= 0,078±0,005.
Уравнение (10) свидетельствует, что модуль,
полученный с помощью уравнения (12), является «мгновенным» объемным модулем,
который есть верхний предел адиабатического объемного модуля и он примерно на
10 % больше изотермического объемного модуля Na. Приведенные в работе результаты согласуются с вышеизложенными.
Кроме того, малые расхождения свидетельствуют о том, что приближение (10)
является приемлемым для таких вычислений.
Можно далее рассчитывать в том же приближении с
помощью уравнения (12). Вариация энергии Хартри дает результат 0,105, и это
также согласуется с экспериментом, если мы примем во внимание верхний предел
реальной сжимаемости. В случае кристаллического состояния поправка к энергии
Хартри дает существенный вклад, необходимый для достижения согласия с
экспериментом. Полученная в расчете точность в целом не хуже, чем для кристалла,
и может быть объяснена примерно тем же образом, как и ранее. Одно из возможных
объяснений касается существенной модификации псевдопотенциала при малых q, о
чем говорилось выше. Это подтверждается расчетом с членами третьего и
четвертого порядка, т.е. включением триплетных и квадрупольных эффективных
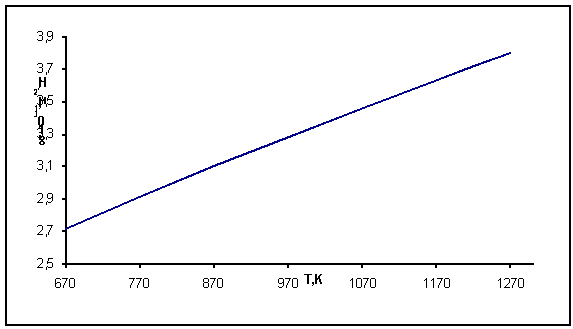
взаимодействий. Это подтверждается расчетными политермами адиабатической
сжимаемости для жидкого свинца (рисунок 1). Адиабатическая сжимаемость при этом
монотонно возрастает. Такое поведение сжимаемости в основном характерно для
металлических расплавов. Таким образом, можно заключить, что мгновенный
динамический модуль, рассчитанный в модели парного приближения, идентичен
динамическому модулю, вычисленному в полной теории во втором порядке, а также
заметно отличается от статического модуля, с одной стороны, и рассчитанного в
теории второго порядка – с другой. Первый из них хорошо согласуется с
изотермическим экспериментальным модулем, тогда как второй требует введения
поправки к энергии Хартри. Тем самым ситуация не отличается от той, которая
имела место при аналогичных расчетах для кристаллического состояния вещества.
Возможное объяснение
состоит в пренебрежении членами электрон-ионного взаимодействия более высокого
порядка, чем второй, а также неудовлетворительностью модификации
псевдопотенциала посредством поправки к энергии Хартри, что приводит к
корректному результату только в длинноволновом пределе. Приведенные соотношения
позволяют нам вычислить сжимаемость
расплавов. Теоретические вычисленные политермы сжимаемости для селена,
теллура, германия и кремния приведены соответственно на рисунках 1, 2, 3, 4, 5.
Модель микронеоднородного расплава с кластерами одинаковых размеров при
фиксированной температуре, конечно, идеализирована. На самом деле в реальном
расплаве могут содержаться кластеры различных размеров. Существование
кластеров не только вблизи температуры кристаллизации, но и при более высоких
температурах, в расплавах полуметаллов и полупроводников обусловлено наличием в
них двух типов химической связи - ковалентной и металлической [1].
Рис. 1 - Политермы сжимаемости расплава свинца
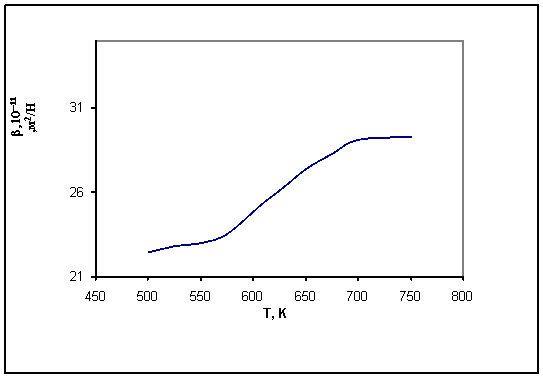 Рисунок 2 - Политермы сжимаемости расплава
селена
Рисунок 2 - Политермы сжимаемости расплава
селена
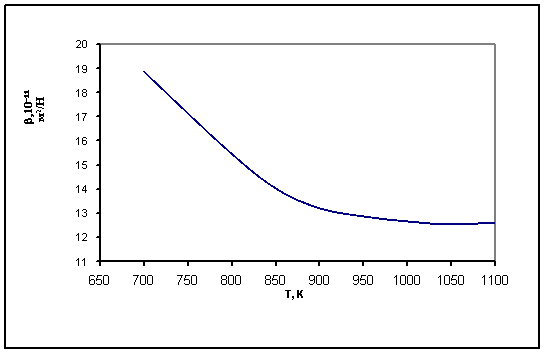 Рисунок 3 - Политермы сжимаемости расплава
теллура
Рисунок 3 - Политермы сжимаемости расплава
теллура
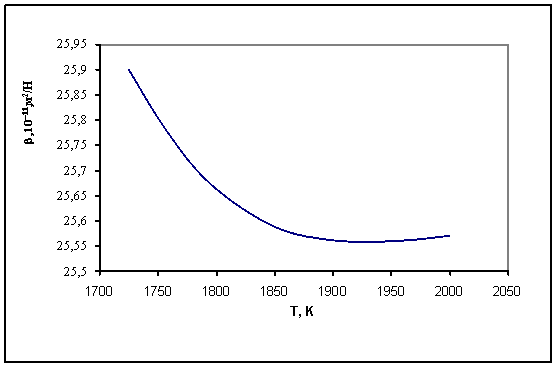 Рисунок 4 - Политермы сжимаемости расплава
кремния
Рисунок 4 - Политермы сжимаемости расплава
кремния
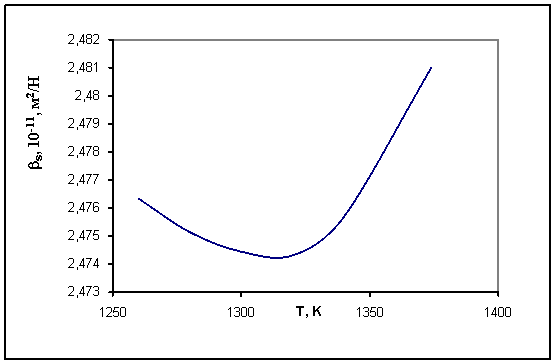 Рисунок 5 - Политермы сжимаемости расплава
германия
Рисунок 5 - Политермы сжимаемости расплава
германия
Ковалентный
тип связи, имеющийся и преобладающий в кристалле, при переходе его в жидкое
состояние не может исчезнуть ни сразу после плавления, ни при дальнейшем
нагреве. Эти связи заложены в саму природу атомов, образующих полуметаллы и
полупроводники, во внешней электронной оболочке атомов и не могут исчезнуть совсем ни при каком агрегатном
состоянии вещества. Вопрос лишь в степени проявления их. Если эти связи
сосуществуют со связями, сильно различающихся по энергии, то они проявляются
существенно. Пример - молекулярные жидкости. Если эти связи погружены в
матрицу других типов связи, энергетически не очень отличающихся по сравнению с
ними, то индивидуальность их нивелируется на уравнивающем фоне близких по
энергии, но отличающихся по природе связей, например, металлических.
Таким
образом, двухструктурная кластерная модель расплава (модель смеси кластерной и
атомарной составляющих), отражающая возможность равновесного сосуществования
двух типов химической связи (ковалентной и металлической), различных по
природе, но близких по прочности (термодинамический аспект), и два механизма
термического распада кластеров (кинетический аспект) позволяют качественно
верно объяснить основные виды экспериментальных и теоретических политерм
сжимаемости в расплавах полуметаллов и полупроводников.
Разнообразие
форм политерм сжимаемости в электронных расплавах требует типизации, ибо их
анализ позволяет разъяснить механизм процессов агрегации и растворения
протяженных объектов в расплавах.