Физика
/1.Теоретическая физика
Твердохлебов
К.А.
Государственный
морской университет имени адмирала Ф.Ф.Ушакова,
Россия
Понятие о квантовой статистике Бозе – Эйнштейна
Квантовая статистка – раздел
статистической физики, исследующей системы, которые состоят из огромного числа
частиц, подчиняющихся законам квантовой механики. Её основная задача состоит в
нахождении равновесного, то есть наиболее вероятного, распределения частиц. А
одним из важнейших объектов изучения является идеальный газ. Это связано с тем,
что во многих случаях реальную систему можно приближенно считать идеальным
газом [1] .
Статистика Бозе
- Эйнштейна - это квантовая
статистика, применяемая к системам тождественных частиц, образованных бозонами
- частицами с нулевым или целым спином в единицах ![]() . Предложена в 1924 индийским физиком Ш. Бозе (Sh.
Bose) для фотонов и в том же году развита А. Эйнштейном (A. Einstein)
применительно к молекулам идеального газа [2].
. Предложена в 1924 индийским физиком Ш. Бозе (Sh.
Bose) для фотонов и в том же году развита А. Эйнштейном (A. Einstein)
применительно к молекулам идеального газа [2].
В данной статистике бозоны рассматриваются
как идеальный газ, то есть считается, что между частицами нет взаимодействия.
Бозоны не подчиняются принципу запрета Паули, поэтому на них не накладываются
ограничения на число частиц, которые могут находиться в данном квантовом
состоянии. Для бозонов характерно то, что вероятность возникновения бозона в
состоянии, где уже имеется n частиц, пропорциональна n.
То есть бозоны "любят"
накапливаться в одном квантовом состоянии [3].
Распределение бозонов по энергиям следует
из так называемого большого канонического распределения Гиббса с переменным
числом частиц при условии, что число тождественных бозонов в данном квантовом
состоянии может быть любым. Это распределение называется распределением Бозе –
Эйнштейна [4].
Вывод и описание распределения Бозе –
Эйнштейна.
Гамильтониан системы невзаимодействующих
частиц равен сумме гамильтонианов отдельных частиц. Собственные функции
гамильтониана системы представляются как произведение собственных функций
гамильтонианов отдельных частиц. А собственные значения (энергия) гамильтониана
системы равна сумме энергий (собственных значений гамильтонианов) отдельных
частиц. Если на данном энергетическом уровне ![]() находится
находится ![]() частиц, то энергия системы есть взвешенная сумма
частиц, то энергия системы есть взвешенная сумма

а волновая функция системы есть
произведение
![]() где
где ![]() - волновая функция для энергетического уровня
- волновая функция для энергетического уровня ![]() .
.
Общая формула вероятности состояния
системы с данным энергетическим уровнем определяется следующим образом
![]()
где ![]() - кратность вырождения данного уровня энергии
[4].
- кратность вырождения данного уровня энергии
[4].
Для описанной выше волновой функции
перестановка координат меняет волновую функцию, то есть перестановка координат
создает новое микросостояние. То есть выбор такой волновой функции предполагает
микроскопическую различимость частиц. Однако макроскопически они соответствуют
одному и тому же состоянию. Поэтому для такой волновой функции при
характеристике макросостояний необходимо вышеуказанную формулу разделить
на ![]() для исключения
многократного учета одного и того же макросостояния в статистической сумме [5].
для исключения
многократного учета одного и того же макросостояния в статистической сумме [5].
Однако, необходимо учесть, что, как
известно, произвольная линейная комбинация волновых функций тоже является
решением уравнения Шредингера. В силу тождественности частиц, то есть их
микроскопической неразличимости, необходимо выбрать такую линейную комбинацию,
чтобы перестановка координат не меняла волновую функцию, то есть
![]()
где Р - операция перестановки координат частиц. Кроме
того, по теореме Паули для бозонов волновые функции симметричны, то есть
умножение на минус единицу координат также не меняет волновую функцию. Такие
волновые функции описывают невырожденные состояния, поэтому ![]() . Кроме того, отпадает вышеуказанная
необходимость деления на
. Кроме того, отпадает вышеуказанная
необходимость деления на ![]() , поскольку для выбранной волновой функции
перестановки не приводят к новым микросостояниям. Таким образом, окончательно
можно выразить вероятность данного состояния следующим образом через числа
заполнения
, поскольку для выбранной волновой функции
перестановки не приводят к новым микросостояниям. Таким образом, окончательно
можно выразить вероятность данного состояния следующим образом через числа
заполнения ![]() :
:
![]()
Отсюда можно показать, что:
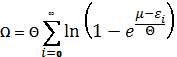
Среднее число частиц в заданном состоянии
можно выразить через эту величину как частную производную с противоположным
знаком по ![]() условно полагая, что
условно полагая, что ![]() различаются
для каждого
различаются
для каждого ![]() . Тогда для среднего числа частиц в заданном состоянии
согласно статистике Бозе — Эйнштейна, получаем
. Тогда для среднего числа частиц в заданном состоянии
согласно статистике Бозе — Эйнштейна, получаем
![]()
где ![]() ,
, ![]() – среднее
число бозонов в квантовом состоянии с энергией
– среднее
число бозонов в квантовом состоянии с энергией ![]() ,
, ![]() – постоянная
Больцмана,
– постоянная
Больцмана, ![]() – абсолютная
температура,
– абсолютная
температура, ![]() – химический
потенциал;
– химический
потенциал; ![]() не зависит от энергии, а определяется только
температурой и плотностью числа частиц. Он определяет изменение внутренней
энергии системы при добавлении к ней одной частицы при условии, что все
остальные величины, от которых зависит внутренняя энергия (энтропия, объем),
фиксированы [6].
не зависит от энергии, а определяется только
температурой и плотностью числа частиц. Он определяет изменение внутренней
энергии системы при добавлении к ней одной частицы при условии, что все
остальные величины, от которых зависит внутренняя энергия (энтропия, объем),
фиксированы [6].
Если ![]() , то распределение Бозе – Эйнштейна переходит в
класическое распределение Максвелла – Больцмона:
, то распределение Бозе – Эйнштейна переходит в
класическое распределение Максвелла – Больцмона:
![]() где A – параметр вырождения, он равен
где A – параметр вырождения, он равен ![]() .
.
Научный руководитель: к.п.н., доцент С.А. Мищик
Литература:
1. Ландау Л. Д., Лифшиц E. M.,
Статистическая физика, ч. 1, 3 изд.,М., 1976. — С. 584.
2. Майер Дж., Гепперт-Mайер M.,
Статистическая механика, пер. с англ., 2 изд., M., 1980, гл. 7. — С. 546.
3. Xуанг К., Статистическая механика, пер с
англ., M., 1966. — С. 521
4.Боголюбов H. H., Лекции по квантовой
статике. Избр. труды, т. 2, К., 1970 Д. H. Зубарев. — С. 523.
5.Трофимова Т.И., Курс физики, 8-е изд., М.,
2004. — С. 434-436
6. Бозе — Эйнштейна статистика // Бари —
Браслет. — М. : Советская энциклопедия, 1970. — Большая советская энциклопедия
: [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 3. — С. 640.