Технические науки/3.Отраслевое машиностроение.

К.т.н Айкеева А.А.¹, д.т.н. Жаутиков Б.А.², магистрант Роговая К.С.¹, магистрант Жаутиков Ф.Б.³, студент Мухтарова П.А.⁴, студент Оспанов А.Е.⁵

¹ Карагандинский Государственный Университет им. академика Е.А. Букетова, Казахстан;

² Атыраусский Государственный Университет им. Х.Досмухамедова, Казахстан;

³ Карагандинский Государственный Индустриальный Университет, Казахстан;

⁴ Азиатский Тихоокеанский Университет Инноваций и Технологий, Малайзия;

⁵ Карагандинский Государственный Технический Университет, Казахстан.

Динамический анализ основных характеристик элементов электромагнитной подъемной установки

Данная работа направлена на построение имитационной модели элементов системы «скип-постоянный магнит-катушка» электромагнитной подъемной установки. В работе представлен и описан принцип работы элементов электромагнитной подъемной установки. Для моделирования использовалась программа ANSYS Maxwell. Задача моделирования: определение основных магнитных характеристик элементов установки (силы Лоренца, напряженности магнитного поля и магнитной индукции). В работе описаны пять экспериментов, по рассчитанным параметрам которых построены общие графические диаграммы. По результатам экспериментов составленные инженерные уравнения с несколькими переменными. Полученные уравнения позволяют определить рассчитываемые в работе характеристики магнитного поля.

Ключевые слова: электромагнитная подъемная установка, «скип-постоянный магнит-катушка», ANSYS Maxwell, индукция магнитного поля, сила Лоренца, напряженность магнитного поля.

Процесс имитационного моделирования процессов взаимодействия элементов электромагнитной подъемной установки, защищенной инновационным патентом №27177 «Электромагнитная подъемная установка (варианты)»[1], преследует своей целью без дорогостоящих экспериментов расчетным путем определять оптимальные и рациональные параметры системы. Современные возможности компьютеров и прикладных программ позволяют полностью реализовывать системный подход к описанию многофакторных динамических состояний органически взаимосвязанных звеньев единой динамической системы «скип – постоянный магнит - катушка»[2,3].

В ходе исследований была разработана модель движения скипа в стволе шахты. Данная модель основывается на эффекте магнитной левитации. Суть метода состоит в том, что на скипе или под скипом располагаются постоянные магниты, а по всей высоте ствола шахты предлагается расположить витки катушки. В этом случае скип с постоянными магнитами движется в стволе сквозь катушку. При прохождении постоянных магнитов через катушку возникает магнитное поле, которое позволяет скипу развить скорость, тем самым двигая его вверх [4,5,6].

При разработке модели данного исследования свойства материалов задаются из библиотеки программы ANSYS Maxwell. Материалом для постоянного магнита был выбран элемент NdFeB (неодим-железо-бор). Это класс редкоземельных магнитов, изготавливаемых прессованием или литьем из интерметаллида Nd2Fe14B. Преимуществами этого класса магнитов являются высокие магнитные свойства (B, H и (B-H)max), а также невысокая стоимость. В связи со слабой коррозионной устойчивостью обычно покрываются медью, никелем или цинком. В нашем случае магниты предполагаемо должны быть покрыты никелем. Материалом для обмоток катушки была выбрана медь. Дополнительно выбирались размеры скипа и катушки[7,8].

Исследовались 5 моделей с различными геометрическими параметрами скипа и катушки. Начальный эксперимент проводился на модели малого размера. Исходные данные для разработки имитационных моделей указаны в таблице 1, геометрические параметры моделей указаны в таблице 2.

Таблица 1 - Исходные данные для разработки имитационных моделей

Вид модели	Элемент	х, см	у, см	z, см	dх, см	dу, см	dz, см	tдвиж, c
Начальная модель	Скип	0	0	-1	0	1,4	1	8
	Катушка	0	1,5	-2,5	0	2,5	2,5	0
Модель 1	Скип	0	0	-1	0	1	1	8
	Катушка	0	1,1	-2,5	0	2,1	2,5	0
Модель 2	Скип	0	0	-1	0	0,6	1	8
	Катушка	0	0,7	-2,5	0	1,7	2,5	0
Модель 3	Скип	0	0	-1	0	1,8	1	8
	Катушка	0	1,9	-2,5	0	2,9	2,5	0
Модель 4	Скип	0	0	-1	0	2,2	1	8
	Катушка	0	2,3	-2,5	0	3,3	2,5	0

Таблица 2 - Геометрические параметры имитационных моделей

Вид модели	Радиус скипа, см	Высота скипа, см	Внутренний радиус катушки, см	Внешний радиус катушки, см	Высота катушки, см
Начальная модель	1,4	2	1,5	2,5	5
Модель 1	1	2	1,1	2,1	5
Модель 2	0,6	2	0,7	1,7	5
Модель 3	1,8	2	1,9	2,9	5
Модель 4	2,2	2	2,3	3,3	5

В ходе исследования основными параметрами, которые необходимо определить, являлись показатели вектора магнитной индукции B, напряженности магнитного поля H и силы Лоренца J. Первые характеристики указывают основные параметры магнитного поля. Сила Лоренца направлена по оси z, согласно размещению катушки в стволе шахты. Пример расчета с определением параметра J показан на рисунке 1.

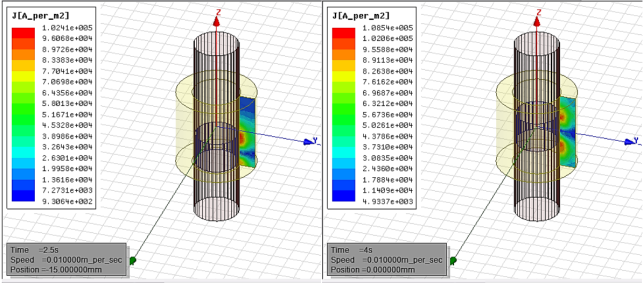
а) б)

а) на 2,5 секунде движения скипа; б) на 4 секунде движения скипа

Рисунок 1 – Результаты расчета силы Лоренца начальной модели

На рисунках 2 и 3 представлены этапы решения модели, в которых определяются характеристики индукции и напряженности магнитного поля. Для полноты картины взаимодействия представлен момент нахождения скипа 2,5 секунде движения и в середине ствола шахты, то есть на четвертой секунде движения. На цветной диаграмме слева указаны значения характеристики от самой минимальной при взаимодействии, выделенной синим цветом, до самой максимальной, выделенной красным цветом.

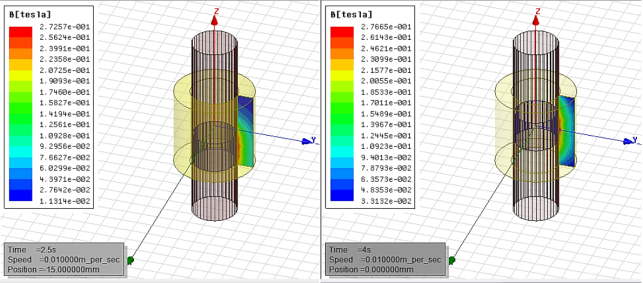
а) б)

а) на 2,5 секунде движения скипа; б) на 4 секунде движения скипа

Рисунок 2 - Результаты расчета магнитной индукции B начальной модели

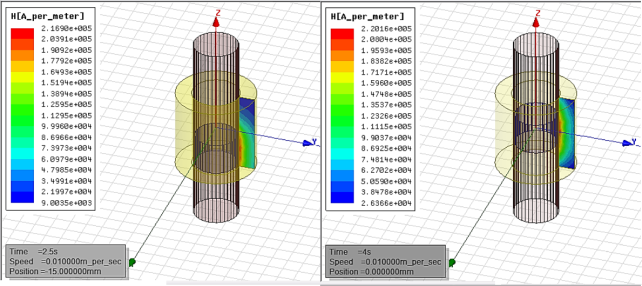
а) б)

а) на 2,5 секунде движения скипа; б) на 4 секунде движения скипа

Рисунок 3 - Результаты расчета напряженности магнитного поля начальной модели

В начальном этапе на каждой секунде модели показано взаимодействие массива из постоянных магнитов на скипе с катушкой в стволе шахты. В соответствии с расположением скипа на модели картина взаимодействия изменяется. По вышеописанной методике были исследованы 5 моделей с различными геометрическими параметрами. По результатам решения построены семейства кривых B, H и J каждой модели. Данные для построения выбраны исходя из максимальных параметров в каждой секунде проводимого исследования.

На рисунке 4 представлено семейство зависимостей параметров силы Лоренца от времени всех пяти экспериментальных моделей. Как видно из графика, самые высокие и низкие значения силы Лоренца наблюдаются у модели 4. У данной модели при решении были заданы самые большие геометрические параметры. Самые малые максимальные и минимальные значения параметров силы Лоренца наблюдаются у модели 2. У данной модели при решении были заданы самые малые геометрические параметры. Таким образом, зависимость геометрических параметров прямо пропорциональна результатам силы Лоренца. Чем больше значение геометрических величин, тем больше максимальные и минимальные значения силы Лоренца. Такая же картина наблюдается и на рисунке 5, где представлена зависимость параметров силы Лоренца от перемещения скипа по оси Z. Чем больше геометрические параметры скипа, тем больше значения силы Лоренца.

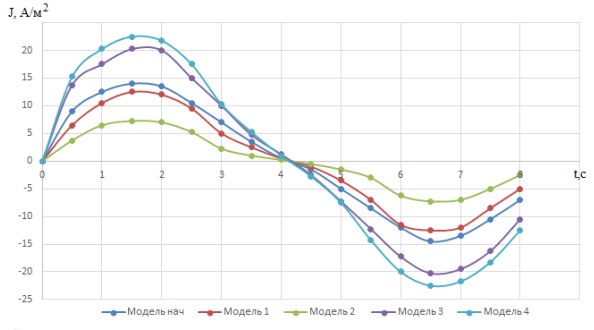
Рисунок 4 - Семейство зависимостей силы Лоренца от времени

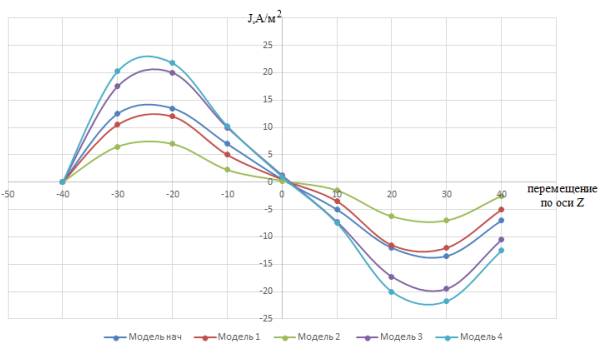
Рисунок 5 - Семейство зависимостей силы Лоренца от перемещения по оси Z

На рисунке 6 представлено семейство зависимостей параметров напряженности магнитного поля от времени всех пяти экспериментальных моделей. Как видно из графика, самые высокие и низкие значения напряженности магнитного поля наблюдаются также у модели 4. Самые малые максимальные и минимальные значения параметров напряженности магнитного поля наблюдаются у модели 2. У данной модели при решении были заданы самые малые геометрические параметры. Таким образом, зависимость геометрических параметров пропорциональна результатам напряженности магнитного поля. Чем больше значение геометрических величин, тем больше максимальные и минимальные значения параметра H. На рисунке 7 наблюдается более плавная картина. Здесь не видно пиков в модели 4, так как скачки величин происходили в половинные доли секунд, а позициям перемещения по оси Z в данном случае соответствуют целые доли секунд. Поэтому в данном случае зависимость обратно пропорциональная. Чем больше или меньше геометрические параметры скипа, тем плавнее представлены на графике перепады максимальных и минимальных значений напряженности магнитного поля. То есть параметры будут выше у модели 1 и 3, у которых относительно всех моделей геометрические значения были по величине вторые и четвертые соответственно.

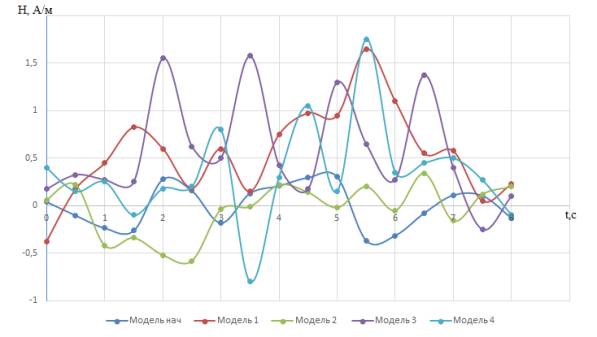
Рисунок 6 - Семейство зависимостей напряженности магнитного поля от времени

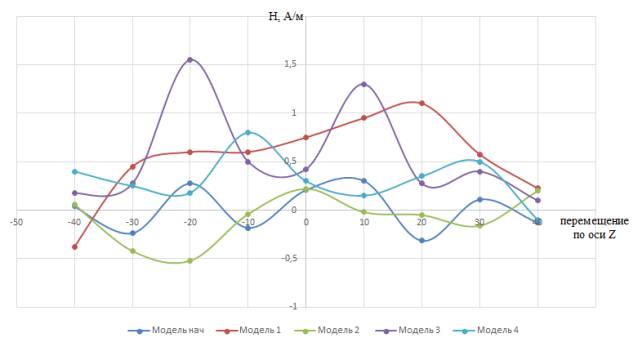
Рисунок 7 - Семейство зависимостей напряженности магнитного поля от перемещения по оси Z

На рисунке 8 представлено семейство зависимостей параметров индукции магнитного поля от времени всех пяти экспериментальных моделей. Как видно из графика, самые высокие и низкие значения магнитной индукции наблюдаются у модели 4. Самые малые максимальные и минимальные значения параметров индукции магнитного поля наблюдаются у модели 2. Таким образом, зависимость геометрических параметров пропорциональна результатам магнитной индукции B. Чем больше значение геометрических величин, тем больше максимальные и минимальные значения параметра B. На рисунке 9 наблюдается более плавная картина. Здесь не видно пиков в модели 4, так как скачки величин происходили в половинные доли секунд, а позициям перемещения по оси Z в данном случае соответствуют целые доли секунд. Поэтому в данном случае зависимость обратно пропорциональная. Чем больше или меньше геометрические параметры скипа, тем плавнее представлены на графике перепады максимальных и минимальных значений индукции магнитного поля. То есть параметры будут выше у модели 1 и 3, у которых относительно всех моделей геометрические значения были по величине вторые и четвертые соответственно.

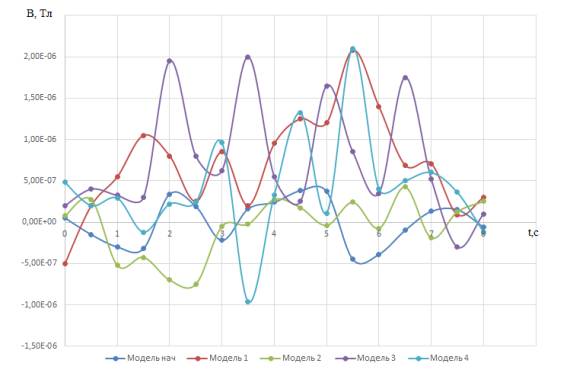
Рисунок 8 - Семейство зависимостей индукции магнитного поля от времени

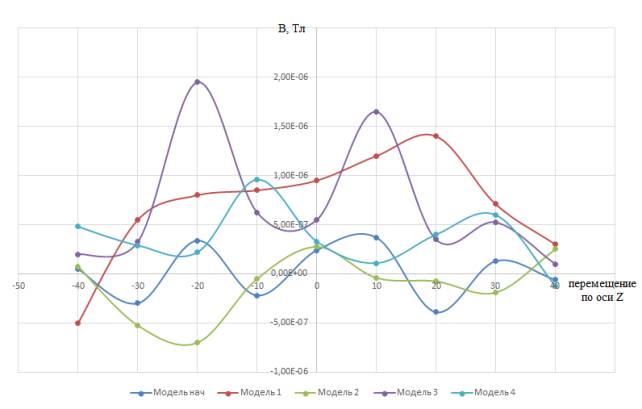
Рисунок 9 - Семейство зависимостей индукции магнитного поля от перемещения по оси Z

C помощью программы определения функциональных зависимостей от нескольких переменных ANETR получены нелинейные зависимости силы Лоренца, магнитной индукции и напряженности магнитного поля на основании параметров начального эксперимента:

J (R_c, h_c, R_{кат внеш}, R_{кат внут}, h_кат, t) = (6.62221E-02 ´ R_c²-1.17237E+00´R_c +

+5.85667E+00) ´ (-6.24003E-03´h_c²+1.86122E-02´h_c+2.69197E+00) ´

´ (2.73563E+00-3.85961E-02´R_{кат внеш}) ´ (2.78227E+00-5.70922E-02´R_{кат внут}) ´

´ (-7.99830E-02´h_кат²+2.49417E-01´h_кат+2.95974E+00) ´ (-2.48646E-02´t²-

-3.20559E-01´t+4.01304E+00)/1.223708E+02,

H (R_c, h_c, R_{кат внеш}, R_{кат внут}, h_кат, t) = (-8.83693E-03´ R_c²+2.40522E+01´R_c+

+1.05605E+01) ´ (1.84315E+01-5.95177E-02´h_c) ´ (1.83474E+01-6.14728E-02´

´R_{кат внеш})´(1.79308E+01-5.74880E-02´R_{кат внут})´(1.81042E+01-4.11898E-02´h_кат)´ ´ (1.88361E+01-1.00375E-01´t)/1.466868E+06,

B (R_c, h_c, R_{кат внеш}, R_{кат внут}, h_кат, t) =(-1.02949E-02´R_c²+2.35418E-01´R_c+

+4.07206E+00)´(4.45300E+00-1.59320E-03´h_c)´(4.81287E+00-7.89474E-02´

´R_{кат внеш})´(4.63128E+00-4.13494E-02´R_{кат внут})´(h_кат/(6.79117E-02+2.45307E-01´

´h_кат)) ´ (2.50443E-02´ t²-5.63115E-01´t+5.76167E+00) / 1.734153E+03.

где J – сила Лоренца, H – напряженность магнитного поля, B – магнитная индукция, R_c – радиус скипа, h_c – высота скипа, R_{кат внеш} – внешний радиус катушки, R_{кат внут} – внутренний радиус катушки, h_кат – высота катушки, t – время движения скипа.

Данная статья написана на основании результатов исследований, выполняемых в рамках грантового финансирования МОН РК по подприоритету «Технологии разработки полезных ископаемых», по теме № 2684/ГФЗ «Обоснование и разработка энергосберегающей технологии выемки горной массы путем создания электромагнитной подъемной установки», а также по приоритету «Энергетика и машиностроение» по теме № 0686/ГФ4 «Разработка системы автоматического управления и комплексной защиты энергосберегающей электромагнитной подъемной установки».

Литература:

1. Инновационный патент на изобретение - Электромагнитная подъемная установка (варианты), № 27177 МЮ РК, авторы Жаутиков Б.А., Айкеева А.А., Жаутиков Ф.Б., Мухтарова П.А.

2. Айкеева А.А. Имитационное моделирование динамики уплотняющих устройств в шахтных пневмоподъемных установках. // Materiały iv międzynarodowej naukowi-praktycznej konferencji «strategiczne pytania światowej nauki – 2008».- Przemśl: Wydawca Nauka I studia, 2008. - Т.9. – С. 30-34.

3. Казаков Ю.Б., Щелыкалов Ю.Я. Исследование магнитного поля в воздушном зазоре стартера СТ230Б.//Тезисы докл. н.-т. конф. /Иванов, энергетич. ин-т. - Иваново, 2008, с. 129.

4. Чигарев А.В., Кравчук А.С., Смалюк А.Ф. ANSYS для инженеров: Справ, пособие. - М.: Машиностроение-1, 2004. - 512 с.

5. Айкеева А.А., Жаутиков Б.А., Роговая К.С., Жаутиков Ф.Б., Мухтарова П.А. Применение компьютерного моделирования для выбора параметров электромагнита //Автоматика и информатика КарГТУ 2015

6. Aikeyeva A.A., Zhautikov B. A., Rogovaya X.S., Zhautikov F.B, Mukhtarova P.A. 3-D modeling of elements of skip-electromagnet system// Eurasian Physical Technical Journal. – Караганда: Изд-во КарГУ, 2015 (в печати)

7. Айкеева А.А., Жаутиков Б.А., Жанасбаева А.С., Мухтарова П.А. Исследование нагрузок на скип шахтной и карьерной электромагнитной подъемной установки// Вестник Карагандинского государственного Университета - Караганда: Изд-во КарГУ, 2015. .№3(79) –С.90-95

8. Айкеева А.А., Жаутиков Б.А., Жаутиков Ф.Б., Мухтарова П.А. The research loads on the skip of mine and quarry electromagnetic lifting installation // Eurasian Physical Technical Journal. – Караганда: Изд-во КарГУ, 2015.№1 (23) –С.59-64.