Студент Павловська К.В., ассистент Коваленко М.А.
Національний технічний університет України

«Київський політехнічний інститут»

Аналіз електромагнітного поля та теплового режиму однофазного трансформатора

В класичній теорії електричних машин та електромашинобудуванні використовуються класичні підходи до розрахунку та проектування електромеханічних об’єктів. Ці методи базуються на чисельних припущеннях, спрощеннях, використанні простих схем заміщення. Такий підхід не відповідає сучасним вимогам по забезпеченню точного та надійного розрахунку параметрів складних електромеханічних структур. В наш час набув розповсюдження польовий метод розрахунку електромагнітного поля, що використовує основні рівняння електромагнітного поля та метод скінченних елементів для розрахунку значень магнітного поля в вузлах розрахункової сітки.

Теоретичною базою для математичного моделювання електромагнітних полів є рівняння поля, сформовані Максвеллом. Рівняння Максвелла встановлюють взаємозв'язок між векторними польовими функціями, характеристиками джерел поля та фізичними параметрами матеріальних середовищ. У сучасній формі запису ці рівняння мають наступний вигляд:

(1)

(2)

(3)

(4)

(5)

(6)

У наведеній системі позначено: польові функції – вектори напруженості магнітного та електричного полів, вектор магнітної індукції і вектор електричного зміщення ; коефіцієнти, які характеризують фізичні властивості матеріальних середовищ – магнітна проникність μ, електропровідність γ, діелектрична провідність ε; щільність електричних зарядів ρ.

Вираз (6) дозволяє знайти густину струмів , обумовлену сумою доданків різної фізичної природи. Доданок обумовлює індуковану щільність струму в електропровідному середовищі; доданок – щільність струму діелектричного зміщення. Доданок визначає щільність струму, яка викликана сторонніми ЕРС; доданок характеризує щільність струмів переміщення вільних зарядів.

У загальному випадку будь-яка польова функція є векторної функцією, і кожна її складова залежить від чотирьох незалежних змінних – трьох просторових координат точки і часу.

При розрахунку магнітного поля використовувалося нестаціонарне нелінійне диференціальне рівняння для векторного магнітного потенціалу в рухомому електропровідному середовищі:

₍₇₎

де: μ, σ – магнітна проникність та електропровідність; – вектори швидкості руху середовища та сторонньої густини струму; – диференціальний оператор Набла.

Для розрахунку електромагнітного поля в квазістатичному режимі рівняння (7) набуває наступного вигляду:

(8)

Польовий розрахунок дозволяє багаторазово збільшити продуктивність в порівнянні з традиційною технологією конструювання.

На наступному етапі задаються початкові і граничні умови. Бувають граничні умови трьох типів:

1) граничні умови 1-го роду - це відомі значення польових функцій на межах:

; (5.9)

2) граничні умови 2 -го роду – це відомі значення нормальної похідної польовий функції на межах області:

; (5.10)

3) граничні умови періодичності – ці умови створюються в тих випадках, коли заздалегідь відомо, що розподіл поля періодично повторюється вздовж зворотного напрямку в розрахунковій області.

– умова періодичності; (5.11)

Граничні умови задаються за допомогою зовнішньої області, що обмежує область розрахункової області по двох координатах.

Початкові умови необхідні при вирішенні нестаціонарних задач, що залежать від часу. При цьому необхідно задати початкові умови – значення польовий функції в середині області в початковий момент часу.

; (5.13)

Джерела поля. В трансформаторах джерелами поля є: щільності струмів в обмотках НН і ВН, неоднорідні граничні умови на межі розрахункової області трансформатора.

Як правило, при розрахунку трансформатора задається щільність струму. При цьому вводиться допущення, при якому елементарні провідники обмотки та ізоляція замінюються однією суцільною підобластю, в якій протікає повний струм в обмотці, а реальна щільність струму замінюється еквівалентною:

, (5.15)

де: I_н [a] – амплітуда номінального струму обмотки НН та ВН; W – число ефективних провідників обмотки НН та ВН ; a – число паралельних гілок; S_п [мм2] – площа поперечного перерізу обмотки.

Після всіх математичних перетворень завдання зводиться до вирішення нелінійної системи алгебраїчних рівнянь щодо невідомих значень векторного магнітного потенціалу у вузлах сітки скінченних елементів.

Розрахунок був виконаний для номінального режиму із чисто активним навантаженням.

Іншою задачею являється розрахунок теплового режиму досліджуваного трансформатора.

Для спрощення побудови моделі розглядається лише обмотки НН та ВН відповідно. У тепловій моделі враховуються втрати в магнітному осерді та обмотках.

Додатково, для розрахунку теплової моделі, задаються джерела теплових втрат: для магнітного осердя втрати в магнітному осерді, для кожної з обмоток – відповідні втрати короткого змикання в них.

Крім того, задаються власні значення теплопровідності та питомої теплоємності для кожного із матеріалів трансформатора: охолоджувального повітря, міді обмотки НН та ВН, сталі магнітного осердя стержня та ярма.

Модель теплових процесів із природнім повітряним охолодженням моделюється та записується за допомогою наступного двовимірного рівняння теплового поля:

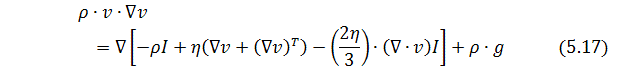
де:

ρ – питома густина матеріалу;

v – оператор, що описує швидкість руху охолоджувального повітря всередині трансформатора;

– оператор Набла;

Т – температура середовища (функція, що обчислюється);

η – величина, що залежить від температури (обчислюється за вбудованими в COMSOL функціями);

g – сила плавучості матеріалу.

Розрахунок теплового поля базується на дотриманні закону теплового балансу середовища і записується у вигляді:

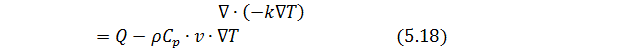
де:

k – коефіцієнт теплопровідності вибраного матеріалу;

С_р – коефіцієнт теплоємності вибраного матеріалу;

Q – теплові втрати в одиниці розрахункового об’єму.

Температура в самій гарячій точці обмотки не перевищує допустиму величину температури для даного класу ізоляції обмоток 60 ⁰С.

Література:

1. Васьковський Ю.М. «Польовий аналіз електричних машин»

2. Тихомиров П. М. "Расчет трансформаторов"