Ýêîëîãèÿ / 2. Ýêîëîãè÷åñêèå
è ìåòåîðîëîãè÷åñêèå ïðîáëåìû áîëüøèõ ãîðîäîâ è ïðîìûøëåííûõ çîí.
PhD Nemtsova À.À.
National
University of Pharmacy, Ukraine
Impact assessment of runoff on river water quality
Land runoff is one of the main diffuse
pollution sources for water bodies. In Ukraine about 80% of total amount of
pollutants are discharged water bodies with runoff. Most of settlements do not
have storm-water sewage systems or these systems cover only some parts of
cities As result not only agriculture runoff and runoff from natural lands are
coming into surface waters, but urban runoff is entered into them directly too.
Unsatisfactory sanitary state of urban areas leads to high level of runoff
pollution. E.g. average content of suspended solids reaches up to 1000 g/m3,
average content of oil products 16 g/m3, and average content of
organic substances (in units of BOD20) 150 g02/m3.
In Ukraine, mainly small rivers represent surface waters. In this case, the
negative influence is doubled, especially for anthropogenic impact of runoff.
Compounds variability and particularly high level of pollutants are
characteristic features of runoff. Runoff characteristics are depended on
watershed area use. E.g. high level of pesticides, nutrients and high dissolved
solids content feature agricultural runoff. Urban runoff usually contains
oil-product additionally However all kinds of runoff are characterized by high
level of organic matter and suspended solids. Suspended solids are the most
characteristic pollutants of land runoff. They exert the major influence on
water quality and on ecological conditions of water bodies. Essential increase
of oxygen consumption by bottom deposits and change of living conditions for
microorganisms in water and deposits reflects this influence. Therefore, impact
assessment of runoff using suspended solids content in watercourses is
necessary.
At the same time suspended
solids content in water body is determined not only by their impact from
external sources, but by sediment transport capacity as well. There is
permanent exchange of suspended solids between water body and bottom deposits.
This fact stimulates specific requirements to calculation methods. At present,
the methods used for impact assessment of runoff on water quality do not allow
taking into account this peculiarity of suspended solids. The aim of this paper
is development of mathematical model, which allow evaluating impact of
non-point sources of pollution on suspended solids content in watercourses.
The mathematical model is
based on the mass conservation principle. One-dimension statement of the
problem is considered. This approach can use for relatively non-wide
watercourses.
Consider an elementary section of
watercourse in the shape of prism. (See Fig. 1)
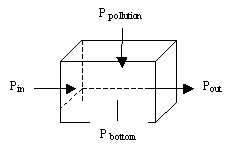
Figure 1. Scheme of mass balance in elementary section of
watercourse.
The mass balance of
suspended solids in the section can be written in the form:
![]() (1)
(1)
Pin = mass of suspended solids is entered into
section through left lateral face per second, g/s.
Pout = mass of suspended solids is coming out section
through right lateral face per second, g/s.
Ppollution = mass of suspended solids is entered into
section through top face with runoff per second, g/s.
Pbottom = Pdown – Pup.
Pdown = mass of suspended solids is settling through
bottom face per second, g/s.
Pup = mass of suspended solids is
entered into section through bottom face in process of re sedimentation per
second, g/s.
Hydraulic characteristics of stream flow for section are assumed to be
constant.
Consider every term in expression (1) separately.
a. Mass of suspended solids is
entered through left lateral face of section. Pin can be
determined as:
Pin = Q×C (2)
Q = flow rate, m3/s.
C = average concentration of
suspended solids on the left lateral face of section, g/m3.
b. Mass of suspended solids is
entered into section by runoff per second. Ppollution can be
determined as:
Ppollution = f×L (3)
f = specific (per the unit
of length of watercourse) entrance of suspended solids into water body per
second, g/(m×s).
L = length of section of watercourse, m.
The value f is obtained as:
f = Qpollution×Cpollution (4)
Qpollution = specific (per unit of
watercourse length) discharge of runoff from watershed area, m3/s.
Cpollution- concentration of suspended solids in runoff,
g/m3.
c. Alteration of suspended
solids mass as a result of water body and bottom deposits exchange per second. Pbottom
can be determine as:
Pbottom = q×B×L (5)
q = sediment discharge in
the vertical direction, g/(m3×s). B = width of watercourse,
m.
d.
Mass of suspended solids is coming out from section
per second. Pout can be determined as:
Pout = Q×(C + DC) (6)
DC = change of average concentration of
suspended solids along watercourse, g/m3 It can be positive or
negative.
The method to obtain the
sediment discharge in the vertical direction depends on degree of saturation of
water flow by suspended solids. The value of resedimentation concentration is
usually used as criteria of saturation by suspended solids. Stream flow is
sediment over laden if the average concentration of suspended solids in water
body is more than concentration of sediments. Otherwise, the stream flow is
normal.
The value of
resedimentation concentration can be determined by Karaushev's empirical
formula (Karaushev, 1977):
![]() (7)
(7)
N and h are non-dimensional
parameters. They can be determined as:
![]() (8)
(8)
Sh = Shezi's coefficient, m1/2/s.
g = the acceleration due to gravity, m2/s.
Sediment discharge in the
vertical direction for normal stream is formed under influence of two major
factors: sedimentation of suspended solids and resedimentation as result of
turbulent exchange between water body and bottom deposits.
Mass of suspended solids that
settle out from volumetric element of water body to unit area of bottom is determined as product of
two factors: settling velocity of suspended fractions and average concentration
of suspended solids.
Mass of suspended solids that rise
from bottom deposits to water body under the influence of the turbulent
exchange can be assumed proportionate to difference between concentration of
resedimentation and average concentration of suspended solids in water body
(Karaushev, 1987).
Thus, the value of sediment discharge in vertical direction is evaluated
from formula
![]() (9)
(9)
u = settling velocity, m/s.
k = dimensional coefficient of proportion, m/s.
Value of the coefficient k is found from relationship
![]() (10)
(10)
G = non-dimensional hydro
mechanical parameter of sediments. Value of this parameter depends on
value of Shezi's coefficient (Sh) and non-dimensional parameter G = u/v. Values of hydro
mechanical parameter are indicated in Table
1.
Table 1. Values of hydro mechanical parameter G
|
G |
Sh |
||||
|
20 |
30 |
40 |
50 |
60 |
|
|
0,0001 |
0,998 |
0,9950 |
0,9600 |
0,98600 |
0,9800 |
|
0,0010 |
0,960 |
0,9340 |
0,9000 |
0,86000 |
0,8160 |
|
0,0020 |
0,927 |
0,8740 |
0,8120 |
0,74200 |
0,6690 |
|
0,0050 |
0,827 |
0,7160 |
0,6010 |
0,48400 |
0,3870 |
|
0,0100 |
0,687 |
0,5200 |
0,3730 |
0,25900 |
0,1770 |
|
0,0200 |
0,479 |
0,2900 |
0,1690 |
0,09900 |
0,0660 |
|
0,0300 |
0,337 |
0,1680 |
0,0840 |
0,04400 |
0,0260 |
|
0,0400 |
0,254 |
0,1100 |
0,0520 |
0,02600 |
0,0150 |
|
0,0600 |
0,041 |
0,0490 |
0,0188 |
0,00890 |
0,0045 |
|
0,0800 |
0,079 |
0,0231 |
0,0084 |
0,00330 |
0,0015 |
|
0,1000 |
0,044 |
0,0123 |
0,0038 |
0,00143 |
0,0005 |
Substituting relationships
(2) - (6), (9) to (1) and approaching the limit as L ® 0 we obtain the following equation
![]() (11)
(11)
The boundary conditions are C= C0 at L = 0.
Taking into account (10), the solution of the equation (11) can be formulary
as
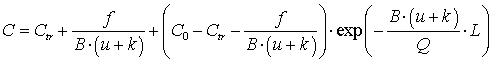 (12)
(12)
C0 = suspended solids
concentration on the left boundary of watercourse section, g/m3.
Ctr = concentration,
corresponding to sediment transporting capacity of stream flow (Rodziller, 1984).
![]() (13)
(13)
For sediment overladen
streamflow (C0 > Cres) only
intensive gravitational settling of suspended solids is characteristic. In this
case, sediment discharge in the vertical direction is introduced in form:
![]() (14)
(14)
The balance equation (11) is reduced and can be
written in the form
![]() (15)
(15)
Its solving is
![]() (16)
(16)
Expressions (12) and (16)
were obtained under assumption that all suspended solids have same settling velocity. The
superposition principle can be used to extend these expressions on real streamflow conditions.
The developed mathematical
model was used for calculation of suspended solids content in the Lopan River (Ukraine). This river
flows through the city of Kharkov (with population about 1,5 million). Part of runoff
non-collected by storm-water drain system discharges river. The discharge from urban
wastewater treatment plant is located at distance 3 km upstream mouth of river. The Lopan River
is the small one. Average long-term flow rate Q = 2,4 m3/s, stream
velocity v = 0,13 m/s, depth of stream h = l m. Wastewater entered into water body leads to increase of
suspended solids content downstream. The average concentration of suspended
solids is 30 mg/l. The average discharge of a runoff is 0,43 m3/s.
The concentration of suspended solids in a runoff from urban area is about 1000
mg/l. Granulometric composition of suspended solids is heterogeneous. They
presented by fine-dyspersated sediments mainly. About 80 % of suspended solids
have a size no more than 0,05 mm, including about 15% of
sediments with diameter less than 0,005 mm. Eight the most representative fractions
can be selected on the basis of long-term observations. Characteristic of
suspended solids granulometric composition is shown in Table 2.
Table 2. Granulometric composition of suspended solids.
|
Diameter, m |
10-3 |
5×10-4 |
2×10-4 |
10-4 |
5×10-5 |
10-5 |
5×10-6 |
10-6 |
|
Hydraulic size, m/s |
10-1 |
6×10-2 |
2×10-2 |
8×10-3 |
2×10-3 |
8×10-5 |
3×10-5 |
8×10-7 |
|
Content for river, % |
25,3 |
15,8 |
28,9 |
10,2 |
4,6 |
4,2 |
5,0 |
6,0 |
|
Content for runoff, % |
0 |
5 |
5 |
10 |
25 |
40 |
7 |
8 |
The main hydromechanical
characteristics of streamflow for each fraction - concentration of
resedimentation Cres and concentration, corresponding to sediment
transporting capacity of stream Ctr - were calculated by
relationships (7), (13) respectively. Results of calculation are presented in
Table 3.
Table 3. The main hydromechanical
characteristics of streamflow by fractions.
|
Diameter, m |
10-3 |
5×10-4 |
2×10-4 |
10-4 |
5×10-5 |
10-5 |
5×10-6 |
10-6 |
|
Cres, mg/l |
11,62 |
7,26 |
13,28 |
4,69 |
2,11 |
1,93 |
2,30 |
2,76 |
|
Ctr, mg/l |
1,2×10-4 |
1,4×10-4 |
0,20 |
0,66 |
1,01 |
2,09 |
2,10 |
2,89 |
The calculations of
suspended solids concentration by the relationships (12), (16) were carried out
for each of eight fractions separately. They have shown that the sedimentation
and resedimentation processes to exercise a significant influence on suspended
solids content. Sedimentation processes dominates for fractions with a diameter
of particles from 0,05 mm to 1,00 mm. Resedimentation processes is more typical
for fine-dyspersated sediments with a diameter from 0,001 mm to 0,005 mm. The
process becomes stabilize at the distance about 200 m from initial point. The
results of calculations for some fractions are shown on Fig. 2.
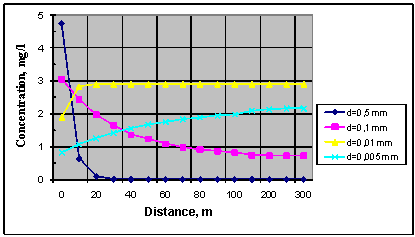
Figure 2. Change of suspended solids
concentration for different fractions.
Total concentration of
suspended solids, obtained on the basis of the superposition principle, shown
that incoming of runoff leaded to increasing of suspended solids content on
10,8% in compares with sediment transporting capacity of stream. The results of
calculation were compared with five-year field data. (See Fig. 3) and confirmed
adequacy of the model.
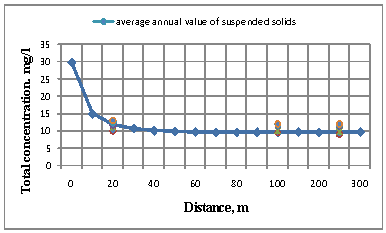
Figure 3. Comparison of calculated suspended solids
concentration with field data
REFERENCES
Karaushev A V (1977). Theory and methods of calculation of river
sediments, Gidrometeoizdat, Leningrad, 272 p. (In Russian).
Karaushev A V (1987). Metodological
fundamentals of assessment and reglamentation of anthropogenic impact on
surface water quality, Gidrometeoizdat, Leningrad, 250 p (In Russian).
Rodziller I D (1984).
Forecasting of water quality of water bodies, Strojizdat, Moskow, 263 p. (In
Russian).
Nemtsova A.A., Ponomarenko E.G. (2012). Use of balance and one-component models for assessment of river water quality. Materials of
International Scientifical-Practical Conference “The Science and education in 21 century”.
Vol. 40. Ecology. Sofia. p. 3-8.