The honored science and education member of the RANS, corresponding-member of the IAS of HS, Dr.S. (eng.). Professor, Pil E.A. Russia, Saint-Petersburg, Saint-Petersburg State Marine Technical University

VARIANTS OF MACROECONOMY DEVELOPMENT AFTER BEING AFFECTED BY INTERNAL AND EXTERNAL FORCES

When affected by external or internal forces (or by both of them combined), economic shells deform, and their deformation can be sorted into the following types presented in the table.

At the simultaneous expansion (retraction) of economic shells (or at their expansion and retraction combined) it is implied that it may take place proportionally, i.e. according to one mathematical law and by one and the same relative value percentagewise, as well as disproportionally, i.e. according to different mathematical laws and by different values percentagewise.

Complex deformation of an economic shell is understood as deformation during which there is simultaneous influence of external and internal forces applied to different locations. That said in one or several areas the economic shell retracts under the influence of external forces, and in one or several locations it expands under the influence of internal forces. In this case external and internal forces affecting the economic shell may be similar or different in value.

As forces P_V affecting an economic shell may differ in their relative value, let us introduce the following three levels for them:

· P_b is a major external (internal) force;

· P_m is a medium external (internal) force;

· P_s is a minor external (internal) force.

Let us set the force value as P_V with the “-” sign for external forces that retract an economic shell so that it deforms and its volume decreases. If an economic shell is affected by internal forces, let us consider them positive, i.e. with the “+” sign, as in this case the economic shell also deforms, but its volume increases. In order not to complicate further description, we will omit the “+” sign.

Hereafter in diagram descriptions there will be the “forces” term which will imply both forces and force. This is done in order not to complicate the description.

Now let us give definitions to all the three forces.

The major external (internal) force P_b is a force under whose influence an economic shell deforms significantly and receives at least one fracture.

The medium external (internal) force P_m is a force under whose influence an economic shell deforms significantly, but in this case it does not receive any fractures.

The minor external (internal) force P_s is a force under whose influence an economic shell deforms slightly.

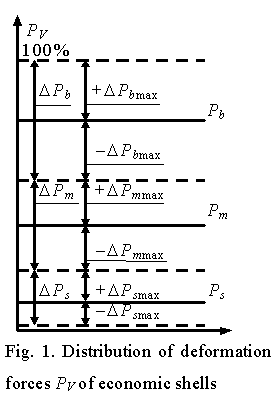
Fig. 3 presents the distribution view of the deformation force P_V of an economic shell on whose basis we can deduce the following formulas (1-3)

DP_b = +DP_bmax + ï-DP_bmaxï, (1)

DP_m = +DP_mmax + ï-DP_mmaxï, (2)

DP_s = +DP_smax + ï-DP_smaxï, (3)

where: DP_i is the value of the deformation force P_V of an economic shell. Hereafter we will understand the “force P_V” term as forces similar in value and affecting an economic shell homogeneously which is shown below on the figures;

+DP_max is the maximum deviation of the value of deformation force P_V of an economic shell increasingly;

-DP_max is the maximum deviation of the value of deformation force P_V of an economic shell decreasingly;

Thus, the value of deformation force P_V of an economic shell can be presented by the following equation (4)

P_V = DP_b + DP_m + DP_s = +DP_bmax + ï-DP_bmaxï + (+DP_mmax) + ï-DP_mmaxï + (+DP_smax) + ï-DP_smaxï = 100%. (4)

Here we must specify that the values of DP_b exceed the values of DP_m and exceed by many times those of DP_s, i.e. DP_b > DP_m, DP_h >> DP_s, and that said the values of DP_b must change in time much rarer than those of DP_m, and far much rarer than those of DP_s. Otherwise, the economic system will be unstable and face often economic perturbations in the form of world economic crises. Moreover, it is difficult to imagine that every month there might be such laws adopted or such cataclysms happening that would lead to this state of the economic shell.