Экономические науки/8. Математические методы в экономике
Ст. преподаватель кафедры высшей
математики Козлова Н.Г.
Студентка гр. МЭ-32 Бондаренко К.
Карагандинский экономический
университет Казпотребсоюза, Казахстан
Применение
кластерного анализа для классификации стран по укрупненной структуре экономики
Главное назначение
кластерного анализа – разбиение множества исследуемых объектов и признаков на
однородные в соответствующем понимании группы или кластеры. Это означает, что
решается задача классификации данных и выявления соответствующей структуры в
ней. Методы кластерного анализа можно применять в самых различных случаях, даже
тогда, когда речь идет о простой группировке, в которой все сводится к образованию
групп по количественному сходству.
Большое достоинство
кластерного анализа в том, что он позволяет производить разбиение объектов не
по одному параметру, а по целому набору признаков. Кроме того, кластерный
анализ в отличие от большинства математико-статистических методов не накладывает
никаких ограничений на вид рассматриваемых объектов, и позволяет рассматривать
множество исходных данных практически произвольной природы.
Попадание в один или разные кластеры объектов
определяется понятием расстояния между Хi и Хj. В данной работе будем использовать квадрат евклидова
расстояние, которое определяется по формуле:
![]()
Для пересчета расстояний между кластерами используются
следующие методы: «ближнего соседа», «дальнего соседа», средней связи.
Рассмотрим применение кластерного анализа для
классификации стран входящих в Еразийский экономический союз. В таблице приведены
данные по доли промышленности и сельского хозяйства в ВВП за 2013г. для данных
странах необходимо провести классификацию с помощью метода кластерного анализа.
|
№ |
Страна |
Доля промышленности в ВВП, % |
Доля сельского хозяйства в ВВП, % |
|
1 |
Армения |
16,8 |
18,9 |
|
2 |
Беларусь |
27,2 |
7,9 |
|
3 |
Казахстан |
27,0 |
4,4 |
|
4 |
Киргизия |
16,1 |
15,2 |
|
5 |
Россия |
25 |
3,2 |
Составлена авторами на основе данных
Статкомитета СНГ.
Первоначальный графический анализ показал, что
данные пять стран можно разбить на два кластера: 1) Беларусь, Казахстан и
Россия; 2) Армения, Киргизия (Рис.1).
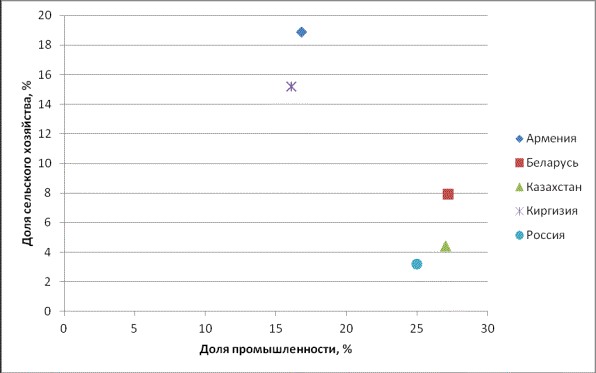
Рис. 1.
Проверим этот вывод с мощью кластерного анализа и
для пересчета расстояний между группами будем использовать метод ближнего
соседа. Метод ближнего соседа заключается в том, что расстояние между
кластерами определяется как расстояние между самими близкими объектами из
рассматриваемых кластеров.
В следующей таблице приведена матрица расстояний,
определенных с помощью квадрата евклидова расстояния:
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
229,16 |
314,29 |
14,18 |
313,73 |
|
2 |
229,16 |
0 |
12,29 |
176,5 |
26,93 |
|
3 |
314,29 |
12,29 |
0 |
235,45 |
5,44 |
|
4 |
14,18 |
176,5 |
235,45 |
0 |
223,21 |
|
5 |
313,73 |
26,93 |
5,44 |
223,21 |
0 |
Первоначально каждый объект считаем отдельным
кластером. На последующих этапах близкие кластеры объединяются в один. Близкие
кластеры определяем с помощью минимального межкластреного расстояния. Процедура
объединения кластеров повторяется, пока все объекты не сформируют один кластер.
Так как изначально анализируется 5 объектов, следовательно, для завершения
процедуры кластеризации потребуется 4 шага.
1 Шаг. Минимальное расстояние
5,44 между кластерами 3 и 5 (Казахстан и Россия) их и объединим в один кластер
и пересчитаем новые межклассовые расстояния.
Столбец и строка соответствующие 3 объекту аннулируются. При пересчете новой
матрицы расстояний необходимо пересчитывать только расстояния до нового
кластера. Расстояния между кластерами, не участвующими в объединении на данном
шаге, не изменяются. В результате получаем следующую матрицу расстояний между
кластерами.
|
|
1 |
2 |
3+5 |
4 |
|
1 |
0 |
229,16 |
313,73 |
14,18 |
|
2 |
229,16 |
0 |
12,29 |
176,5 |
|
3+5 |
313,73 |
12,29 |
0 |
223,21 |
|
4 |
14,18 |
176,5 |
223,21 |
0 |
2 Шаг. Минимальное расстояние
12,29 между кластерами 3+5 и 2 (Казахстан,
Россия и Беларусь) их и объединим в один кластер и аналогичным образом
пересчитаем новые расстояния.
|
|
1 |
2+(3+5) |
4 |
|
1 |
0 |
229,16 |
14,18 |
|
(2+3)+5 |
229,16 |
0 |
176,5 |
|
4 |
14,18 |
176,5 |
0 |
3 Шаг. Минимальное расстояние
14,18 между кластерами 1 и 4 (Армения и
Киргизия) их и объединим в один кластер и пересчитаем новые расстояния.
|
|
1+4 |
(2+3)+5 |
|
1+4 |
0 |
176,5 |
|
(2+3)+5 |
176,5 |
0 |
4 Шаг. Объединение всех объектов в один кластер [(1+4)]+[(2+3)+5].
Процесс кластеризации
прекращается в том случае, когда минимальное расстояние между кластерами резко
увеличивается. В нашем случае резкое изменение происходит на последним шаге с
14,18, до 176,5. Следовательно, нам нецелесообразно проводить объединение на последнем
шаге кластеров (1+4) и (2+3)+5 в один. Таким образом, после проведения анализа
с помощью метода ближнего соседа с использованием квадрата евклидовой метрики
были получены два кластера: 1+4–
Армения, Киргизия и 2+(3+5) – Беларусь, Казахстан, Россия.
Использую для пересчета
расстояний между кластерами методы дальнего соседа и средней связи были
получены аналогичные разбиения стран на группы.
Следует отметить широкое
использование кластерного анализа, не только в экономике, но и в различных
других отраслях знаний. Очень часто кластерный анализ применяется в маркетинге
для проведения сегментации рынка или потребителей, в психологии для разбития
людей по психотипу, в биологии для классификации живых существ, в медицине и
т.д.
Список литературы:
1. Дубров A.M.,
Мхитарян B.C., Трошин Л.И. Многомерные статистические
методы. - М.: Финансы и статистика, 2003.
2.
Межгосударственный
статистический комитет СНГ. [Электронный ресурс]– Режим доступа:
http://www.cisstat.com/