Белес А.О., Тленова А., Абдиева З.А.

Шымкентский университет, Казахстанский инженерно-педагогический университет Дружбы народов, Шымкент, Казахстан

Об одной постановке задачи линейного программирования

Введение. Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Особенно широкое распространение линейное программирование получило в экономике, так как исследование зависимостей между величинами, встречающимися во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные [1].

Формулировка задачи. Даны линейная функция

(1)

и система линейных ограничений

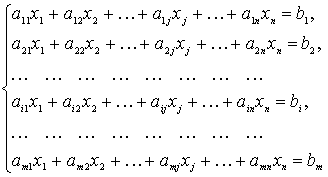(2)

(3)

где , и – заданные постоянные величины.

Найти такие неотрицательные значения которые удовлетворяют системе ограничений (2) и доставляют линейной функции (1) минимальное значение. В системе ограничений (2) все можно считать неотрицательными. Общая задача имеет несколько форм записи.

Векторная форма записи. Минимизировать линейную функцию при ограничениях

(4)

где ; ; - скалярное произведение; векторы

, , ...,

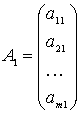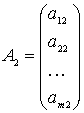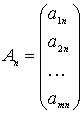
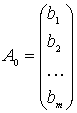
состоят соответственно из коэффициентов при неизвестных и свободных членов.

Определение 1. Планом или допустимым решением задачи линейного программирования называется вектор удовлетворяющий условиям (2) и (3).

Определение 2. План называется опорным, если векторы , входящие в разложение (4) с положительными коэффициентами являются линейно независимыми. Так как векторы являются -мерными, то из определения опорного плана следует, что число его положительных компонент не может превышать .

Определение 3. Опорный план называется невырожденным, если он содержит положительных компонент, в противном случае опорный план называется вырожденным.

Определение 4. Оптимальным планом или оптимальным решением задачи линейного программирования называется план, доставляющий наименьшее (наибольшее) значение линейной функции.

В дальнейшем рассмотрено решение задач линейного программирования, связанных с нахождением минимального значения линейной функции. В тех задачах, где необходимо найти максимальное значение линейной функции, достаточно заменить на противоположный знак линейной функции и найти минимальное значение последней функции. Заменяя на противоположный знак полученного минимального значения, определяем максимальное значение исходной линейной функции. Свойства решений задачи линейного программирования тесно связаны со свойствами выпуклых множеств.

Пример. [2] Для изготовление двух видов продукции , используют три вида сырья: , и . Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, приведены в табл.1. Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль [2].

Обозначим через количество единиц продукции , а через -количество единиц продукции . Тогда, учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья получим систему ограничений

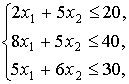
которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысить имеющихся запасов. Если продукция не выпускается, то , в противном случае . То же самое получаем и для продукции . Таким образом, на неизвестные и должно быть наложено ограничение неотрицательности: , .

Таблица 1

Вид сырья	Запас сырья	Количество единиц сырья, идущих на изготовление единицы продукции.
	20 40 30	2 8 5	5 5 6
Прибыль от единицы продукции в тенге		50	40

Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции - выразим как функцию двух переменных и Реализация единиц продукции вида и единиц продукции вида P₂ дает соответственно и тенге прибыли, суммарная прибыль (тенге).

Условиями не оговорено неделимость единицы продукции, поэтому и (план выпуска продукции ) могут быть и дробными числами, следовательно, задача имеет бесконечное множество вариантов планов (значений и , которые удовлетворяют системе ограничений).

Необходимо найти такие неотрицательные значения и , при которых функция достигает максимума, т.е. найти максимальное значение линейной функции при ограничениях

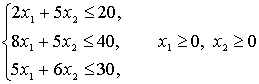
Построенная линейная функция называется функцией цели и совместно с системой ограничений образует математическую модель рассматриваемой экономической задачи.

Литература

1. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. –М.: Высшая школа, 1980. –300 с.

2. Куракбаев Д.С., Ибрагимов О.М., Куракбаева С.Д. Основы линейного программирования. Электронный учебник. / Гос.регистр. в Комитете по правам интеллект. собст. МЮ РК №1569 от 15.10.2010.