Математика/1. Дифференциальные и интегральные уравнения

К.ф.-м.н. Тингаев А.А.

Одесский торгово-экономический институт КНТЭУ, Украина

Свойства решений сингулярного уравнения 2-го порядка при простых корнях характеристического уравнения

Solutions properties of second order singular equation with simple real roots of characteristic equation. This article contains the investigation of conditions on which singular second order differential equations have solutions that satisfy to the set estimation. The sufficient conditions of existence of such solutions are obtained.

Свойства решений сингулярного уравнения 2-го порядка при различных действительных корнях характеристического уравнения. Изучается проблема существования решений сингулярных дифференциальных уравнений 2-го порядка, удовлетворяющих заданной оценке. Получены достаточные условия существования таких решений.

Постановка задачи. Изучение асимптотических свойств решений дифференциальных уравнений и систем принадлежит к наиболее актуальным задачам качественной теории дифференциальных уравнений, к которым, как известно, сводятся математические модели механики, электротехники, атомной и ядерной физики, физической химии, математической биологии и других областей науки. Направления исследований таких уравнений и их систем достаточно разнообразны. Во многих случаях новая задача требует собственных, не традиционных подходов и доказательств фундаментальных теорем.

Анализ последних достижений. Теория дифференциальных уравнений второго порядка в достаточно полном виде появилась в прошлом веке (библиографию можно посмотреть в [1]). Актуальность практических применений повлияла на появление многих видов дифференциальных уравнений второго порядка, которые исследуются по нынешнее время. Данная статья есть продолжение работы [2].

Цель статьи. Провести изучение вопроса о существовании решений сингулярных дифференциальных уравнений 2-го порядка, удовлетворяющих заданной оценке вблизи точки сингулярности. Получить достаточные условия существования таких решений в случае асимптотически различных действительных корней характеристического уравнения.

Изложение основного материала. Рассмотрим уравнение вида

(1)

где на (0;∆]; 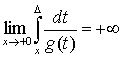при ∆ > 0;

, , при x→+0.

Обозначим , . Положим

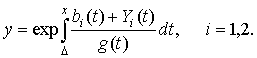
Как и в [2], решения уравнения (1) ищутся в полном нормированном пространстве Х_y функций в котором

a) , где , (2а)

b) . (2b)

Положим поочередно 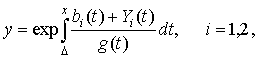где Y_i(t) – новые неизвестные функции вместо y(x). Тогда, заметив, что

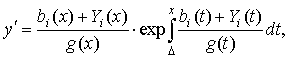
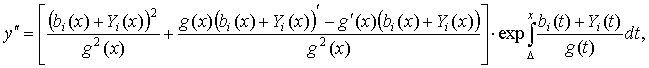
получим для Y₁(t) сингулярное интегро-дифференциальное уравнение

(3)

где .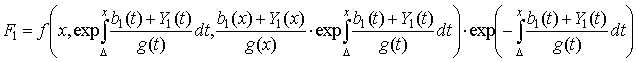

Введём класс функций :

.

Дальнейшие рассуждения основаны на принципе неподвижной точки Шаудера ([3]) и топологическом принципе Важевского ([4]).

Теорема 1. Пусть

1) дифференциальное уравнение

()

удовлетворяет условиям теоремы существования и единственности непрерывного решения в области

D₁ =

2) , причём что на [0;∆]:

3) такое, что в D₁

а) равномерно ограничены функции , и

б) при x→+0:

Тогда уравнение (3) имеет хотя бы одно решение при соответствующем α.

Возвращаясь к уравнению (1), получаем, что оно имеет по крайней мере одно решение такое, что на (0;∆]:

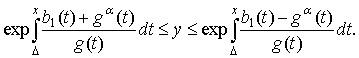
Доказательство.

Доказательство аналогично случаю асимптотически равных корней (см. [2]). Заметим только, что в условиях теоремы .

Рассуждая таким же образом, лишь заменяя Y₁(t) на Y₂(t), получим уравнение

(4)

Введём класс функций :

.

Теорема 2. Пусть

4) дифференциальное уравнение

()

удовлетворяет условиям теоремы существования и единственности непрерывного решения в области

D₂ =

5) , причём что на [0;∆]:

6) такое, что в D₂

а) равномерно ограничены функции , и

б) при x→+0: : 

Тогда уравнение (4) имеет интегральное многообразие размерности единица из при соответствующем β.

Замечание

В условиях теоремы 2 . Отсюда, согласно топологическому принципу Важевского ([4]) сделан вывод о существовании интегрального многообразия уравнения (4) размерности единица, в отличие от существования хотя бы одного решения уравнения (3).

Перспективы исследования. Изучается вопрос о существовании решений сингулярных дифференциальных уравнений 2-го порядка, удовлетворяющих заданной оценке вблизи точки сингулярности в случае асимптотически различных комплексных корней характеристического уравнения.

Литература

1. Рейссиг Р, Сансоне Г., Конти Р. Качественная теория нелинейных дифференциальных уравнений. М., Наука, 1974.-320 с.

2. Тингаев А.А. Свойства решений сингулярного уравнения 2-го порядка при равных корнях характеристического уравнения // Новейшие научные достижения. – 2014. Том 28. София. «Бял ГРАД-БГ» - с.3-8

3. Хартман Ф. Обыкновенные дифференциальные уравнения: Пер. с англ. - М.: Мир, 1970. - 720 с.

4. Wazewski T. Sur une principe topologique de l'examen asymptotique des integrales des equations differentielles//Ann. Soc. Polon. Math. - 1947. - Vol. 20, №8.- Р. 279-313.