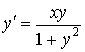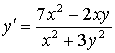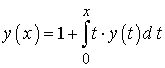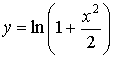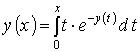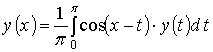Математика / Дифференциальные и интегральные уравнения

к.т.н. Нікулін О.В., к.ф.-м.н. Наконечна Т.В.

Дніпродзержинський державний технічний університет, Україна

Дніпропетровський національний університет ім. О. Гончара, Україна

Тести відповідності для диференціальних та

інтегральних рівнянь

Важливою складовою математичної підготовки у вищих навчальних закладах є вивчення теорії звичайних диференціальних та інтегральних рівнянь, яка потім широко використовується при математичному моделюванні. З цього приводу при модульної організації процесу навчання в планах і робочих навчальних програмах по диференціальним рівнянням, а також інтегральним рівнянням, як правило, відводяться окремі змістовні модулі. В їх рамках проводяться контрольні роботи, а також інші види контролю успішності, отже, питання планування тестування з диференціальних та інтегральних рівнянь є актуальними.

За результатами огляду відомих варіантів задач і тестів можна зробити висновок, що у більшості випадків спостерігається закрита форма тестів [1] або їх тісний зв'язок з індивідуальними розрахунковими завданнями [2,3]. Перевірка успішності розв'язання тестів визначає лише достатній рівень або потрібна трудомістка перевірка розв’язків викладачами, причому сам процес вирішення студентами – трудомісткий. В результаті можливі сумніви в повноті та репрезентативності перевіреного засвоєння розділів курсу.

Метою роботи вибрано вдосконалення структури та змісту тестів з диференціальних (ДР) та інтегральних рівнянь (ІР), щоб забезпечити їх репрезентативність, зниження трудомісткості розв'язання і можливість автоматизації перевірки. З урахуванням педагогічних і психологічних аспектів тестування використовуються напрацювання незалежного зовнішнього оцінювання з математики. У модульну контрольну роботу включаються закриті тести, тести відповідності та тести з короткою числовою відповіддю. У порівнянні з варіантами контрольних з [4] в кожен з них додаються тести відповідності [5]. Їх проектування і побудова має методичне та практичне значення.

Пропонуються варіанти оцінювання успішності освоєння диференціаль-

них та інтегральних рівнянь з двадцяти структурних одиниць кожний. З них на тести відповідності відводиться вісім одиниць, тобто два завдання.

Прийнята форма тестового завдання на відповідність складається з двох множин, на які поділяються задачі з розв’язками та розташованих ліворуч і праворуч робочого поля. При випробуванні студент повинен встановити зв'язок між елементами множин, заповнивши клітинки таблиці згідно інструкції. Рядки таблиці відповідають елементам заданої множини, а стовпці – елементам, що підлягають вибору. Якщо студент встановлює наявність відповідності між елементами множин, то на перетині відповідних рядків і стовпців ставиться позначка, наприклад "" або "". Можна розглянути типові приклади.

 Тест відповідності для ДР. Для даних диференціальних рівнянь першого порядку (1– 4) встановити їх тип (А – Д). Результати занести в таблицю. Позначки правильних відповідей на питання  проставляються на перетині відповідних рядків (цифри) і колонок (букви).

Рівняння	Тип		А	Б	В	Г	Д
1.	А однорідне рівняння	1
		2
2.	Б лінійне рівняння	3
		4
3.	В рівняння Бернуллі
4.	Г рівняння у повних диференціалах
	Д рівняння з відокремлюваними змінними

Розв’язок завдання. Таблиця відповідностей :

	А	Б	В	Г	Д
1
2
3
4

Розв’язання.

 1. Перетворимо рівняння до виду , який відповідає визначенням в теорії диференціальних рівнянь, тобто . Отже, маємо лінійне рівняння. Обираємо тип  Б. 

2. Перетворимо рівняння до виду , який відповідає визначенням в теорії диференціальних рівнянь, тобто . Отже, маємо рівняння з відокремлюваними змінними. Обираємо тип Д.

 3. Перетворимо рівняння до виду ,  який відповідає визначенням в теорії диференціальних рівнянь, тобто . Отже, маємо рівняння Бернуллі. Обираємо тип  В. 
 4. Перетворимо рівняння до виду  , який відповідає визначенням в теорії диференціальних рівнянь, тобто . Отже, маємо однорідне рівняння. Обираємо тип  А.  

За отриманими результатами заповнюємо таблицю.

Тест відповідності для ІР. Установіть відповідність між інтегральними рівняннями (1–4) та функціями (А – Д), які є їх розв’язками. Результати занести в таблицю. Позначки правильних відповідей на питання проставляються на перетині відповідних рядків (цифри) і колонок (букви).

Рівняння	Розв’язок		А	Б	В	Г	Д
1.	А	1
		2
2.	Б	3
		4
3.	В
4.	Г
	Д

Розв’язок завдання. Таблиця відповідностей:

	А	Б	В	Г	Д
1
2
3
4

Розв’язання.

1. Диференціюємо інтегральне рівняння. Отримуємо . Після відокремлення змінних та інтегрування знаходимо загальний розв’язок . З початкового рівняння отримуємо умову . Знаходимо . Обираємо розв’язок В.

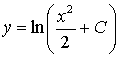2. Диференціюємо інтегральне рівняння. Тоді . Після відокремлення змінних й інтегрування знаходимо загальний розв’язок . З початкового рівняння отримуємо умову . Знаходимо , отже 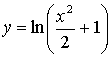. Обираємо розв’язок А.

3. Методом послідовного диференціювання зводимо дане рівняння до диференційного рівняння . Розв’язуючі ЛОДР ІІ знаходимо . Обираємо розв’язок Г.

4. Методом диференціювання зводимо дане рівняння до рівняння

. Розв’язуючі ЛОДР І знаходимо . Після підстановки в інтегральне рівняння знаходимо . Обираємо розв’язок Б.

За отриманими результатами заповнюємо таблицю.

Тести подібної структури проходять апробацію в другому навчальному семестрі першого курсу, доповнюють варіанти контрольних робіт другого модуля з вищої математики [5]. Вирішення проблем модернізації вищої освіти в Україні включає вдосконалення фундаментального навчання, зокрема, з математики. Реалізація відповідних програм вимагає застосування нових або видозмінених методик, в тому числі і при контролі навчальним тестуванням. Розроблені, апробовані, підготовлені для подальшого використання тести відповідності змістовних модулів з диференціальних та інтегральних рівнянь. Готується до публікації перевидання навчального посібника з допрацьованими тестами.

Література

1. Тестові завдання з вищої математики: Навчальний посібник / С.І. Гургула, В.М. Мойсишин, В.О. Воробйова та ін.; За ред. С.І. Гургули, В.М. Мойсишина. – Івано - Франківськ: Факел, 2008. – 737 с.

2. Кадильникова Т.М. Вища математика в прикладах та задачах. Частина IV: Навч. посіб. / Т.М. Кадильникова, І.В. Щербина,

П.Г. Хорошманенко – Дніпропетровськ: НМетАУ, 2010. – 96 с.

3. Кривошея С.А. Диференціальні та інтегральні рівняння: Підручник / С.А. Кривошея, М. О. Перестюк, В.М. Бурим. – К.: Либідь, 2004. – 408 с.

4. Шумейко О.О. Модульне і підсумкове оцінювання: тести з вищої математики / О.О. Шумейко, Т.В. Наконечна, О.В. Нікулін. – Дніпропетровськ: «Наука і освіта», 2009. – 172 с.

5. Нікулін О.В. Вища математика: факти і формули, задачі і тести / О.В. Нікулін, Т.В. Наконечна . – Дніпропетровськ: Біла К.О., 2015. – 187 с.