Д.ф.-м.н. Срумова Ф.В.

Таджикский национальный университет

О ПРИНЦИПЕ ЛОКАЛИЗАЦИИ ДЛЯ РЯДОВ ФУРЬЕ ПО ФУНДАМЕНТАЛЬНОЙ СИСТЕМЕ ФУНКЦИЙ ПОЛИГАРМОНИЧЕСКОГО ОПЕРАТОРА

Рассмотрен принцип локализации для рядов Фурье по фундаментальной системе функций полигармонического оператора.

Ключевые слова: ряды Фурье по фундаментальной системе функций полигармонического оператора.

В [1] доказано, что «почти вся» последовательность частичных сумм ряда Фурье по фундаментальной системе функций оператора Лапласа имеет порядок

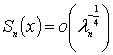
(соответственно .

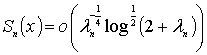Рассматриваемому вопросу посвящены [2-5].

Далее, известна [6] асимптотическая формула для числа собственных значений полигармонического оператора:

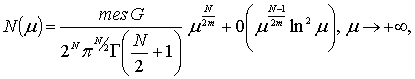(1)

где -произвольная -мерная область, справедливая для краевых условий 1-го, 2-го и 3-го рода.

Учитывая (1), сформируем следующую теорему.

Теорема. Пусть выполнены следующие требования для функции и для фундаментальной системы функций:

1) ; 2) в подобласти области ; 3) для фундаментальной системы функций полигармонического оператора имеет место (1).

Тогда почти всюду в справедлива оценка:

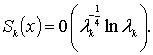(2)

Для доказательства теоремы достаточно установить сходимость почти всюду в ряда

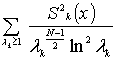(3)

Здесь -тая частичная сумма ряда Фурье функции по фундаментальной системе функций полигармонического оператора.

Доказательство сходимости почти всюду в ряда (3) проводится так же, как и в [1], только при использовании асимптотической формулы среднего значения, установленный в [7], появляются некоторые дополнительные рассуждения.

Введем вспомогательную функцию

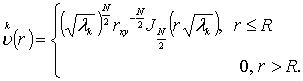
С помощью формулы среднего значения определим коэффициент Фурье этой функции, который имеет вид

где

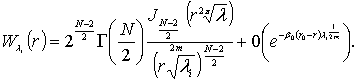
Далее, интегрируя по частям -раз выражение

получаем

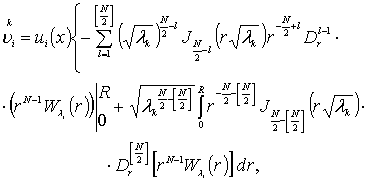
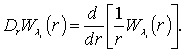(4)

Все подстановки при обращаются в нуль. Так же как и в [1], умножаем (4) на коэффициент Фурье функции , удовлетворяющей условиям теоремы, и производим суммирование по всем от 1 до . В силу свойств функции и и равенства Парсеваля

Лемма. Пусть и в и в пограничной полосе области

равномерно в . Здесь - любое целое число.

Далее, следуя методу [7], учитывая лемму, на основании рассуждений [1], получаем

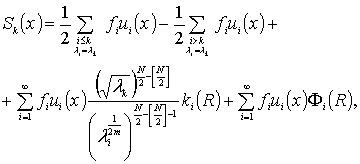(5)

где

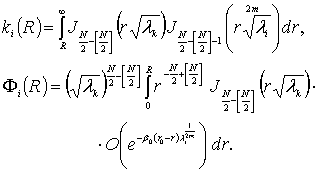
Из (5) вытекает, что достаточно доказать равномерную в сходимость ряда

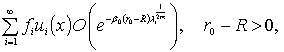
что следует из неравенства Коши-Буняковского и равенства Парсеваля при учете, что

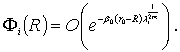
Замечание. Оценка (2) неулучшаемая, нельзя заменить

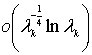на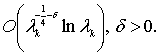

Литература

1. В.А.Ильин «Сиб. матем. ж.», т.9, №5, (1968), 1093-1106.

2. G.H.Hardy, I.E. Littlewood. Comptes Rendus (Paris), 156, (1913), 1307-1309.

3. J.Marcinikiewicz, J.London Math. Soc., 14, (1939), 162-168.

4. G. Alexits, D. Kralik. Magyar tud. akad. Mat. Kutato int közl. 8, N 3, (1964), 317-327.

5. А.Зигмунд. Тригонометрические ряды. «Мир», М., 1965.

6. И.А.Шишмарев. ДАН СССР, т.186 №4, (1969), 781-782.

7. И.А.Шишмарев. Функциональный анализ и его приложения, т.3, вып. 4, (1969), 69-76.