Математика/4. Математическое моделирование

 

Аманбаев Т.Р., Курманалиева А.

Институт математики и математического моделирования, Казахстан,

Южно-Казахстанский государственный университет им. М. Ауэзова

 

Моделирование и расчет течения ультрадисперсной смеси в квазигомогенном приближении

 

Многофазные (или гетерогенные), в частности, двухфазные дисперсные системы часто встречаются в различных областях современной техники и человеческой деятельности. При этом течение таких сред в большинстве случаев сопровождается тепло- и массообменными процессами. Исследование течений гетерогенных сред является одной из актуальных проблем динамики и теплофизики многофазных дисперсных систем [1,2].

В последние годы процессы испарения и конденсации в различных средах стали использовать для получения наноматериалов (в частности при синтезе углеродных нанотрубок), а также для получения наноразмерных (ультрадисперсных) частиц в расширяющихся каналах за счет зародышеобразования (нуклеации) и их роста [3-7]. При этом для описания процесса роста зародышей используются различные модели, в частности, монодисперсная модель, в которой предполагается наличие коагуляции зародышей. В практике часто встречаются процессы, в которых в исходном состоянии рабочая среда является однофазной, например, в виде газа (пара), а в ходе исследуемого процесса создаются условия для появления новой фазы в виде капель [1]. Именно этими процессами определяется начальная стадия фазовых переходов в однофазных (в исходном состоянии) средах (например, в переохлажденном паре). Молекулярно-кинетическая теория процесса гомогенной нуклеации была заложена в работах ряда исследователей [1]. Эта теория основана на том, что в газе в результате флуктуаций концентрации молекул в их хаотическом движении беспрерывно образуются и разрушаются кластеры (микрокапли в переохлажденном паре). Флуктуационное зародышеобразование и дальнейший конденсационный рост кластеров в пересыщенном паре является одним из наиболее важных процессов, приводящих к зарождению и развитию дисперсной фазы. Отметим, что проблема математического описания процесса зародышеобразования (нуклеации) остается актуальной до сих пор. В последнее время она активно обсуждается в связи с задачей роста нанокластеров в дисперсных системах.

Появившиеся в результате нуклеации зародыши жидкой фазы являются достаточно мелкими (наноразмерными) и в связи с этим подвержены броуновскому блужданию. Броуновское блуждание приводит к их взаимному столкновению, поэтому является одним из основных, постоянно действующих механизмов, способствующих коагуляции микрокапель. Коагуляция (слияние) частиц является одной из основных причин эволюции дисперсных систем. Это явление наблюдается в различных физических ситуациях и оказывает воздействие на рост кластеров в растворах, газодисперсных системах. Подробный анализ механизмов, приводящих к движению и столкновению частиц в дисперсных системах, приведен в [8].

Целью данной работы является построение математической модели и проведение расчетов течения смеси газа и зародышей жидкой фазы в канале переменного сечения в двумерной постановке. Рассматривается простейший случай, когда внешние силы, поток тепла извне и трение со стенкой отсутствуют. Считается, что на входе в канал однофазная среда находится в переохлажденном состоянии, когда температура среды ниже температуры насыщения. Кроме того предполагается, что процесс конденсации в метастабильном состоянии пара протекает в две стадии. На первой стадии за счет гомогенной нуклеации появляются зародыши жидкой фазы. Некоторые из них исчезают, а некоторые (размеры которых превышают критического радиуса) растут в дальнейшем за счет броуновской коагуляции и фазовых превращений (конденсации). Ввиду малости размеров зародышей, можно считать, что скорости и температуры дисперсной и несущей фаз совпадают.

Далее будут рассматриваться только сферические кластеры, в которых число молекул  однозначно связано с радиусом кластера

 

 

Здесь  - масса одной молекулы газа, a – радиус кластера. В случае максвелловского распределения молекул по скоростям распределение указанных кластеров по радиусу описывается формулой Гиббса

 

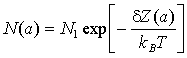
где  - число молекул несущей фазы в единице объема,  - постоянная Больцмана,  T – температура несущей среды,  - так называемая работа создания кластера радиусом a. Работа  равна изменению термодинамического потенциала Гиббса для вещества, входящего в кластер с учетом вклада для создания поверхности жидкой фазы [1]. Используя линейное разложение потенциала Гиббса около состояния насыщения вдоль изотермы для переохлажденного пара получим [1]:

 

,    ,    

 

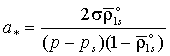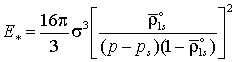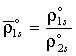
где  - критический радиус зародыша, а  - работа создания критического зародыша.  ,  - истинные плотности газовой и жидкой фаз в состоянии насыщения. Концентрация критических зародышей определяется по формуле

 

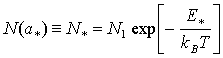
Обычно появление даже небольшого количества жидкости может заметно влиять на параметры течения. Выделение тепла приводит к уменьшению степени перенасыщения, в результате чего образование новых зародышей прекращается, и в дальнейшем кластеризация идет уже на вновь образовавшихся центрах конденсации. Так что все центры конденсации зарождаются, как правило, в самом начале процесса нуклеации, когда имеет место достаточно большое перенасыщение. После этого переход от метастабильного состояния в состояние насыщения может произойти довольно быстро и носить скачкообразный характер. Отсюда следует, что процесс кластеризации в высокоскоростных потоках можно разделить на две стадии. На первой стадии определяющим является процесс образования зародышей критического размера, на второй – процесс конденсационного роста вновь образовавшихся зародышей, когда нуклеацию можно не учитывать. Хотя в ряде случаев одновременно протекают оба процесса, такое разделение представляется вполне разумным.

Анализ процессов уноса и осаждения молекул пара на межфазной границе приводит к формуле Герца-Кнудсена-Ленгмюра для результирующей интенсивности фазовых переходов, а зависимость температуры насыщения фаз от давления удовлетворяет дифференциальному уравнению Клапейрона–Клаузиуса [1], с учетом которого интенсивность фазового перехода может быть выражена через перегрев или переохлаждение. Для моделирования движения двухфазной дисперсной смеси при наличии процессов нуклеации, коагуляции зародышей и фазовых переходов используем уравнения и замыкающие соотношения механики многофазных сред [1,2], которые, учитывая допущения и уравнения, приведенные выше, запишем в квазигомогенном приближении

 

, ,   ,          (1)      

,     ,                                (2)

,  ,   ,   ,          (3)

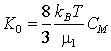 ,   ,   ,    ,         (4) ,      .                                (5)

 

Здесь αi , , ρi , ci – объемные доли, истинные и приведенные плотности, а также теплоемкости несущей (i=1) и дисперсной (i=2) фаз; ρ, p, T, e, E, v – плотность, давление, температура, внутренняя и полная энергии, а также вектор скорости эффективной среды (равновесной смеси газовой и дисперсной фаз);  – интенсивность фазового перехода, отнесенная на единицу площади межфазной поверхности;  – коэффициент коагуляции зародышей, обусловленной их броуновским движением;  - динамическая вязкость несущей фазы; n, a – концентрация и радиус микрокапель;  – поправка Каннингема–Милликена. Газ будем считать калорически совершенным с постоянной теплоемкостью, а вещество конденсированной фазы  – несжимаемым.

Таким образом, система уравнений (1)-(5) вместе с замыкающими соотношениями представляет собой математическую модель течения ультрадисперсной смеси в квазигомогенном приближении при наличии процессов коагуляции и фазовых превращений.

Рассмотрим течение двухфазной газодисперсной смеси в канале с внезапным расширением (рис. 1). При этом учитывая вышесказанное, будем полагать, что на первой стадии из-за процесса нуклеации в узкой части канала непрерывно появляются зародыши жидкой фазы (согласно теории гомогенной нуклеации). Затем при течении сформированной газодисперсной смеси в расширенной части канала осуществляются процессы коагуляции и фазовых переходов. С учетом симметрии течения для постановки задачи зададим следующие граничные условия на входе в расширяющуюся часть канала (h – ширина узкой части канала):

 

x=0, 0≤y≤h/2: , , , , , u=u0, v=0,  .

 

Здесь ,  - критический радиус и концентрация зародышей, отвечающие начальному пересыщению пара на входе в канал. 

Вдоль оси канала примем условие симметрии, на твердых границах – условие непротекания, а на свободной границе – условие непрерывности течения. В качестве начальных условий в расширенной части канала примем условия невозмущенной газовой фазы (без зародышей жидкой фазы).

y
 
                                                 

 

u0
 

0
 

h
 
                                                                            

                                                                                                                                             x        

 

 


Рис. 1

 

Для решения поставленной задачи необходимо использовать численные методы, например, метод крупных частиц, который разработан для решения задач газовой динамики, а впоследствии модифицирован для задач механики многофазных сред [1,2]. Расчеты показали, что течение ультрадисперсной смеси имеет вихревую структуру, причем такая структура перемещается по расширенному каналу, сохраняя свою форму. Также обнаружено, что наиболее крупные капли формируются именно в зоне вихря, причем первоначальный радиус капель за счет процессов коагуляции и конденсации увеличивается на расчетный момент времени более чем в 10 раз. Таким образом, процесс коагуляции существенно влияет на рост кластеров при течении смеси пара и зародышей конденсированной фазы в канале.

 

CПИСОК ЛИТЕРАТУРЫ

1.   Нигматулин Р.И. Динамика многофазных сред. - М.: Наука, 1987.

2.  Ивандаев А.И., Кутушев А.Г., Нигматулин Р.И. Газовая динамика многофазных сред. М.: ВИНИТИ, 1981.

3.  Горбунов В.Н., Муслаев А.В., Пирумов У.Г., Розовский П.В. Неравновесная конденсация паров металла в смеси с инертным газом при расширении в соплах установок для генерации кластерных пучков // Мех. жидк. и газа. – 1995. - №3. – С. 80-91.

4.  Пирумов У.Г. Перспективные методы получения ультрадисперсных частиц в высоскоростных потоках // Проблемы машиностроения и надежности. – 1996. - №1. – С. 94-116.

5.  Аникеев В.И., Степанов Д.А., Ермакова А. Моделирование и расчет процесса быстрого расширения сверхкритического флюида с образованием наночастиц // Теор. основы хим. технол. – 2011. – Т. 45, №2. – С. 155-169.

6.  Weber M., Russell L.M., Debenedetti P.G. Mathematical modeling of nucleation growth formed by the rapid expantion of supercritical solution under subsonic conditions // J. Supercrit. Fluids. – 2002. - Vol. 23. – P. 65-80.

7.   Jun Li, Matos H.A., Gomes de Azevedo E. Two-phase homogenous model for particle formation gas saturated solution process // J. Supercrit. Fluids. – 2004. - Vol. 32. – P. 275-293.

8.    Волощук В.М., Седунов Ю.С. Процессы коагуляции в дисперсных системах. – Л.: Гидрометеоиздат, 1975. – 370 с.