UDC: 62-83:681.3
Ermaganbetova S.*1, Zharkymbekova M2, Toygozhinova
Zh.2, Shadhin Y2
1Al-Farabi
Kazakh national university, Almaty, Kazakhstan
2Almaty University of Energy and Communications, Almaty, Kazakhstan
Definition for stability of motion of system of TPN – AD
by program MatLab
Abstract.The article provides a block diagram of a closed-loop nonlinear system
of thyristor frequency converter -an induction motor with a short-circuited rotor and the
mathematical description of dynamics of system. It is given the
calculation of the phase trajectories of the system in MATLAB.
Definition for stability of motion of the
closed-loop nonlinear system the thyristor voltage converter– an induction
motor is one of necessary problems of projection of this system. The objective stability of motion of
system of TPN– a АD can be solved by Lyapunov's method or method of a harmonic
linearization [1]. However the objective can be also successfully solved by
method of phase trajectories by means of computer MATLAB system on the
Computer.
Key words: induction motor, thyristor voltage converter, block diagram, nonlinear
system, differential equations, stability.
УДК 62-83:681.3
С.Д.
Ермаганбетова*1, М. Б. Жаркымбекова 2, Ж.Ж. Тойгожинова 2,
Ю.И. Шадхин2
1Казахский национальный университет имени
аль-Фараби, г .Алматы, Казахстан
2Алматинский Университет энергетики и связи, г. Алматы, Казахстан
Определение устойчивости движения системы ТПН – АД
в программе MatLab
Абстракт. Определение устойчивости движения замкнутой
нелинейной системы тиристорный преобразователь напряжения – асинхронный
двигатель является одной из необходимых задач проектирования данной системы.
Поставленная задача устойчивости движения замкнутой системы ТПН – АД может быть
решена методом Ляпунова или методом гармонической линеаризации [1]. Однако
поставленная задача может быть также успешно решена методом фазовых траекторий
с помощью компьютерной системы MATLAB на ЭВМ.
Ключевые слова: асинхронный двигатель,
тиристорный преобразователь напряжения, структурная схема, нелинейная система,
дифференциальные уравнения, устойчивость.
УДК 62-83:681.3
С.Д.
Ермағанбетова*1, М. Б. Жаркымбекова 2, Ж.Ж. Тойғожинова 2,
Ю.И. Шадхин2
1Әл-Фараби
атындағыҚазақҰлттық Университеті, Алматы
қ., Қазақстан
2 Алматы энергетика
және университеті, Алматы қ., Қазақстан
MatLab
программасының көмегімен КТТ – АҚ жүйесі
қозғалысының тұрақтылығын анықтау
Абстракт. Статьяда
қысқа тұйықталған роторлы ЖТТ – АҚ
тұйықталған бейсызықты жүйенің
құрылымдық сұлбасы және динамикалық
жүйені математикалық сипаттау келтірілген. MATLAB
бағдарламасында жүйенің фазалық траекториясына
есептеулер жүргізілген.
Түйін
сөздер: асинхронды
қозғалтқыш, кернеуді тиристорлы түрлендіргіш,
құрылымдық сұлба, бейсызықты жүйе,
дифференциалдық теңдеу, орнықтылық.
Introduction.
Phase curve preparation in the ТПН - АД coordinates by which it is defined
stability of motion of this system. Differential equations for
calculating the phase curve. The
experimental data
The experimental data for calculation of
parameters of system of ТPN – АD.
Experimental
The Method of phase
trajectories allows to define stability of system of TPN – АD and
self-oscillations of system that is especially important. The block diagram of
closed-loop nonlinear system of TPN – АD in the MATLAB environment is
illustrated in figure 1.
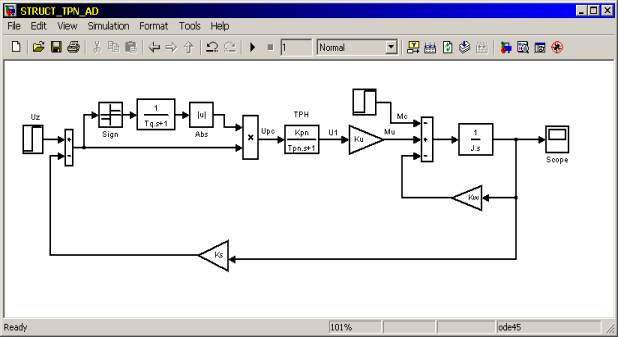
Figure 1. The block diagram of system of TPN – АD with velocity feedback
The block diagram of an induction
motor [2] consists of the integrating component
with
coefficient of a feedback Kw and an inertialess component with coefficient Ku.
The thyristor voltage converter of system is
shown in Figure 1 by inertial
component
). The nonlinear filter with amplitude attenuation [1] is used
as a velocity governor of system for improvement of quality of management
processes. Created differential
equations for research of a dynamic stability of nonlinear system of TPN – АD by method of phase trajectories at Mc=0
(the static moment of loading) formed by:
;
; (1)
,
where 
is
the velocity of the engine; 
is
the output voltage of thyristor voltage convert;
is
the output signal of an inertial component of a velocity governor; 
is the transmitting coefficient of an induction motor; 
is the TPN transmission coefficient; 
is
the feedback coefficient on velocity; 
is the electromechanical time constant of АD; 
is the time constant of ТPN; 
is the time constant of an inertial component of the nonlinear
filter with amplitude attenuation; 
is the setting influence
To calculate the phase trajectory of the phase space of the system of equations (1) on the computer
the equations (1) we can lead to the following
form:
;
(2)
here
Summary
Numerical integration of differential
equations (2) is carried out in MATLAB system[3]. The program of the solution
of the system of equations (2) is illustrated in figure
2.
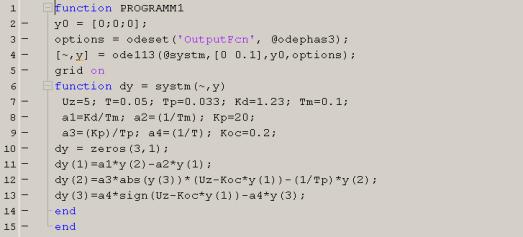
Figure 2.
Program of the solution of the system of equations
In the program coefficients of system of
differential equations (2) are calculated for an induction motor with a
short-circuited rotor type RA132MA6. The phase curve of dynamics of closed-loop
system of TPN – a BP is illustrated in figure 3.
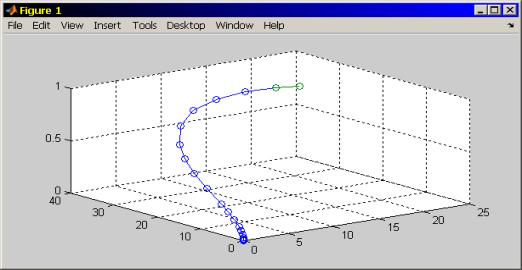
Figure 3. A
phase trajectory of dynamics of clpsed-loop system of TPN – a BP
The
phase trajectory tends to the origin of coordinates of the closed-loop
nonlinear system of TPN – a BP, whic corresponds to stability
of motion of system [4].
REFERENCES
1. Popov E. The theory of
nonlinear systems of automatic control and management. - M .: Science, Ch. Ed.
nat. - mat. lit., 1988.
2. Terekhov V., Osipov O.
Control systems of electric drives. - M .: Publishing center
"Academy", 2008.
3. Anoufriev I., Smirnov A., Smirnov E. MATLAB 7. - SPb .: BHV -
Petersburg, 2005.
4. Besekersky V. Popov E.
The theory of automatic control systems. - SPb.: Publisher
"Occupation", 2004.