Сатыбалдиев О.С., Мекебай Н.А.

 

Қ.И.Сәтбаев атындағы ҚазҰЗТУ, Қазақстан

 

Шекарасында берілген қысымның мәндері бойынша жартылай шексіз облыстағы мұнай қатпарының қысымын анықтау

 

 және  мәндерінде қысымы нөлге тең және  шексіздікке алыстағанда нөлге ұмтылатын, ал қатпардың сол жақ шетінде бірлік қысымды сақтайтын жазық жартылай қатпардағы қысымды анықтау қажет болсын.

Алдымен есеп шартына сәйкес оның математикалық моделін құралық.

                                (1)

теңдеуінің   жазық жартылай қатпар облысының шекарасындағы қысымының мәндеріне сәйкес, яғни

1)  

2)                                                                                                        (2)

3)  шексіздікке ұмтылғанда  нөлге ұмтылады,

4)   шарттарын қанағаттандыратын шешімін табу керек.

Шешімі.  шексіздікке ұмтылғанда  нөлге ұмтылатындықтан

болады. Мұндағы , . (2) теңдіктің 1) - шарты орындалсын деп ұйғаралық. Сонда

,

(2) теңдіктің 2) - шартынан кезкелген  үшін

теңдіктерін аламыз. Соңғы теңдіктен  теңдігі шығады. Олай болса  . Сонымен, әрбір  үшін

 

шешуін аламыз. Лаплас теңдеуі сызықтық теңдеу, сондықтан соңғы шешімдердің қосындылары да осы Лаплас теңдеуінің шешімі болады, яғни

(2) теңдіктің соңғы шартынан

                                      (3)

теңдігін аламыз. (3) теңдікті коэффициенттері

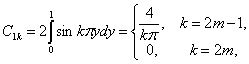
болатын, периодты функцияның синустар бойынша Фурье қатарына жіктелуі ретінде қарастыруға болады.

Сонымен, ізделіп отырған шешіміміз

болады екен.

Тағыда бір есепті қарастыралық.  облысында (1) теңдеудің 

                                                  

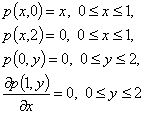
шарттарын қанағаттандыратын шешімін табалық [11].

 

 

17 – сурет. Мұнай қатпарының қысымы

        

 (1) теңдеу  және  шарттарын қанағаттандыруы үшін жоғарыдағы теңдікпен берілген шешімді таңдаған жеткілікті:

.

Үшінші шарттан  және

Мұндағы . Соңғы  теңдіктен

                         

                            

                       (4)

 (4) теңдіктің екінші шартын қанағаттандыру үшін оған парапар формасын жазалық

,

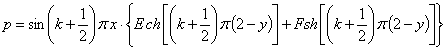Екінші шарттан  екендігі шығады. Демек,

 (5)

(5) теңдікпен анықталған  шешімін  бойынша қосып

.

теңдігін аламыз.

Бірінші шарттан

                                      .                                       (6)

(6) – теңдік  функциясының синустар бойынша Фурье қатарына жіктелуін береді.  Жіктелу коэффициенті

.

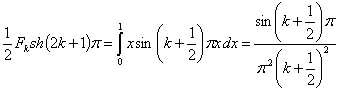Сонымен, іздеп отырған шешіміміз мына түрде жазылады

.

 

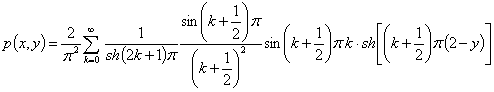Пайдаланылған әдебиеттер

 

1. Яглом И.М. Математические структуры и математическое моделирование. – М., Наука, 2010. -327с.

2. Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов.- М., Мир, 2012. -357с.

3. Гусейнзаде М.А. и др. Применение обобщенных функций в задачах трубопроводного транспорта нефти и газа. – М.:РГУ нефти и газа им. И.М. Губкина, 2011. - 415с.