УДК (ӘӨЖ)  517. 957

  БІР КЛАСТЫ  ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІҢ ШЕШІМДЕРІНІҢ ҚАСИЕТТЕРІН ЗЕРТТЕУ

                            Рахимова Г.Қ. ф.-м.ғ.к.,  Ахан А.Ә. магистрант

 

РЕЗЮМЕ

            В работе рассматриваются существование, гладкость решении  линейных вырождающихся уравнении одного класса в пространстве . При  изучении полученных результатов, сформулировали необходимые и достаточные условия   аппроксимативных свойств полупериодических задач Дирихле для нелинейных вырождающихся уравнений.

SUMMARY

              There are  space the smooth of solutions of the  one class  linear functioning equations  degenerated  are researched. Before research it of coercive solutions of  the high series one class no linear degenerated equations of a Dirichlet semi periodic problem necessary and sufficient conditions were obtained. 

 

Жоғарғы ретті  дифференциалдық теңдеудің шешімінің бар болуы, оның қасиеттерінің тегістілігі, осы жұмыста зерттелген.
            Бұл жұмыста берілген Ω={(x,y):0<x<2π,0<y<1} облысында төмендегі жоғарғы ретті  дифференциалдық теңдеуді

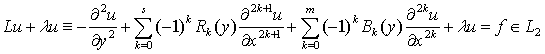,            (1)

 мынадай шектік есепте қарастырамыз:

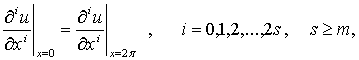                           (2)

                                                                                                             (3)

мұнда   .

         Бұл жұмыстың ерекшелігі, қарастырып отырған есеп, Петровский классификациясына кірмейтін стандартты емес есеп және сонымен қатар ол сызықты  дифференициалдық теңдеу.  Жұмыста алынған негізгі нәтиже ол,  осы дифференциалдық теңдеудің шешімінің бар және жалғыз екендігі көрсетілген.

      Барлық жерде (1) теңдеудің коэффиценттерін төмендегі шектеулер қоямыз:

 бөлікті-үздіксіз функциялар және берілген аргументтері бойынша төмендегі шарттарды қанағаттандырады:

     i) ;

    ii) және [0,1]аралығында кемімейді,  және [0,1] аралығында кемімейді;

  iii) .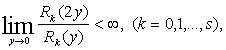

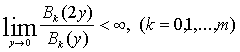- арқылы төмендегі норма арқылы толықтырылған функциялар кеңістігін белгілейміз

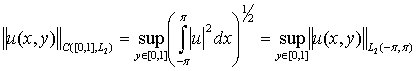     (4)

ал    -төмендегі нормамен алынған функциялар кеңістігін белгілейміз

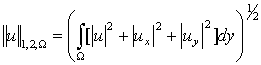               .                              (5)

Анықтама функциясын (1)-(3)  есебінің күшті шешімі  дейміз, егер  табылып, n→∞ жағдайда төмендегі шартты қанағаттандырса

         Теорема 1 Айталық і)-ііі) шарттары орындалсын, онда кез –келген fÎL2 үшін (1)-(3) есібінің L2(Ώ) кеңістігінде жататын жалғыз шешімі бар болады және ол төмендегі теңсіздікті қанағаттандырады

.

Мұндағы   –  кеңістігінің нормасы.

        Теорема 2  Айталық і)-ііі) шарттары орындалсын, онда кез –келген fÎL2 үшін (1)-(3) есібінің L2(Ώ) кеңістігінде жататын жалғыз шешімі бар болады және оған төмендегі баға орындалады

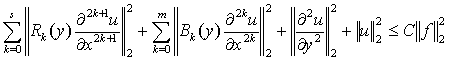,    (6)

мұндағы  С>0- тұрақты сан.

Осындай жоғарғы ретті  дифференциалдық теңдеулердің қолданбалы қасиеттері бар болуына байланысты, яғни газдік динамикада, гидромеханикада және моментсіз қабықшалар теориясында ерекше роль атқарады, сондықтан соңғы жылдары классикалық емес сызықты нұқсанды теңдеулердің жартылай периодты Дирихле есебінің шешімдері және оның тегістілігі актуальді болып табылыды.  Дифференциалды теңдеулерді зерттеу кезінде көбіне көңіл бөлінетін сұрақтар мынадай: шешімнің бар болуы, жалғыздығы, олардың қасиеттері. Дифференциалды теңдеудің шешімінің бар болуы және жалғыздығы шарты нақты жүріп жатқан процестің сипаттауының қажетті шарты болып табылады.    Барлық алынған нәтижелер леммалар мен теоремалар түрінде тұжырымдалған.  Ал леммалар мен теоремалардың  дәлелдеулері көрсетілмеген жағдайда оларға сілтемелер жасалған.

 

ҚОЛДАНЫЛҒАН  ӘДЕБИЕТТЕР ТІЗІМІ

1.      Соболев С.Л. Некоторые применения функционального анализа в математической физике. -М.: Наука, 1988. -336с.

2.      Кальменов Т.Ш., Отелбаев М.О. О гладкости решений одного класса вырождающихся эллиптических уравнений // Дифференциальные уравнения. –1977 – Т. 13. – № 7. – С.1244 - 1255.

3.      Муратбеков М.Б. Коэрцитивные оценки для одного дифференциального оператора высшего порядка // Дифференциальные уравнения. –1981 – Т.17. –  № 5. – С. 893 - 901.

4.      Муратбеков М.Б. О гладкости решений одного класса неравномерно вырождающихся эллиптических уравнений // Известия АН Каз ССР. Серия физико-математическая.- 1981.- № 5. - С. 71 - 73.

5.      Муратбеков М.Б. О гладкости решений одного класса неравномерно вырождающихся эллиптических уравнений высокого порядка // Корректные краевые задачи для неклассических уравнений математической физики.- Новосибирск.- 1981.- С.144 - 146.

6.      Муратбеков М.Б. О гладкости решений вырождающихся эллиптических уравнений и одномерного нелинейного стационарного уравнения Шредингера // Автореферат канд. дисс.  физ.-мат. наук. - Алматы. - 1982. - 16 с.

7.      Муратбеков М.Б. Разделимость и оценки поперечников множеств, связанных с областью определения нелинейного оператора типа Шредингера // Дифференциальные уравнения. - 1991.