УДК 54-142

Кажикенова А.Ш., Алибиев Д.Б., Турдыбеков К.М., Турдыбекова К.М.

Карагандинский государственный университет им. Е.А.Букетова, Казахстан

Математическое моделирование Вязкости расплава кадмия с учетом ассоциации кластеров

Для теоретического описания физико-химических свойств из трех агрегатных состояний вещества наиболее сложным является жидкое состояние. В структуре жидкости пространственное расположение атомов не находится в свободном состоянии, как в газе, но и не закреплено, как в кристалле. Поэтому жидкость по своим свойствам может приближаться к газу вблизи температуры кипения или к твердому телу вблизи температуры плавления.

Вязкость, одна из основных характеристик жидкости, не поддается строгому теоретическому выражению на основании различного учета сил связи частиц, то есть структурных факторов. После многочисленных исследований многие авторы [1] приходят к выводу, что единственно достаточно достоверным источником сведений о вязкости жидких металлов при различных температурах является эксперимент, аналитическое описание которого возможно либо статистическими аппроксимирующими моделями, либо полуэмпирическими моделями с двумя и более подгоночными параметрами. Свойства жидких металлов получены в основном из экспериментальных исследований. Однако, с развитием науки появляется необходимость в новых альтернативных методах исследования свойств расплавов металлов.

Сотрудниками Химико-металлургического института (г. Караганда) была разработана модель температурной зависимости вязкости металлов, основанная на концепции хаотизированных частиц [2]. Авторы концепции предполагают во всех агрегатных состояниях трех видов частиц: кристаллоподвижных, жидкоподвижных и пароподвижных частиц. Согласно концепции, три агрегатных состояния вещества рассматриваются с единой точки зрения по его бесструктурной составляющей, которая численно определяется долей сверхбарьерных и подбарьерных по теплосодержанию в точках плавления RT_m и кипения RT_b частиц согласно распределению Больцмана. Предложенная авторами концепции базовая модель кинематической вязкости определяется влиянием на эту характеристику кристаллоподвижных частиц

, (1)

где в качестве реперной можно использовать не только точку плавления T_m, но и любую другую надежно определенную величину вязкости n_r при T_r.

Авторами данной концепции были предложены еще две модели:

- с учетом кристаллоподвижных и жидкоподвижных частиц

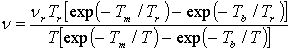, (2)

где T_m и T_b – соответственно температуры плавления и кипения;

- с учетом всех видов частиц:

n 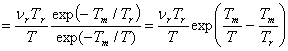. (3)

В ходе дальнейших исследований было установлено, что более сильная зависимость вязкости от температуры может быть объяснена образованием ассоциированных элементарных кластеров, разрушение которых с повышением температуры происходит параллельно с разрушением элементарных кластеров. Авторами данной работы был учтен данный эффект в рамках базовой первой модели путем усиления температурного фрагмента (Т_r/Т) и на этом основании предложена обобщенная математическая модель кинематической вязкости

n = n_r(T_r/T)^a, (4)

где показатель a - степень ассоциации`п-частичных кластеров.

Параметр а может быть определен путем логарифмирования

. (5)

Для определения параметра а целесообразно использовать все экспериментальные значения вязкости при различных температурах за исключением n_r, T_r, приводящего к неопределенности вида [0/0]. Затем находим среднее значение параметра агрегации по формуле:

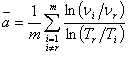. (6)

Полученное среднее значение необходимо проверить на представительность по критерию однородности множества и затем использовать в уравнении (4) для получения расчетных значений и сравнения с экспериментальными по коэффициенту корреляции.

Покажем применение предлагаемой модели на примере расплава кадмия. По кадмию в монографии [1] авторами [3, 4] приводится уравнение для динамической вязкости кадмия для интервала температур 591-840 К:

lnh = - 3,447 + 8,374×10³/Т – 6,109×10⁶/Т² + 1,636×10⁹/Т³, мПа×с. (7)

В справочнике [5] указаны температуры плавления и кипения T_m = 594 K и T_b = 1039 K, значения плотности при трех температурах, данных по вязкости нет. По уравнению (7) и плотности рассчитана кинематическая вязкость, которую сопоставили с расчетными по четырем моделям. Результаты всех расчетов приведены в таблице 1 и на рисунке 1.

Таблица 1 – Сопоставление сглаженных экспериментальных [1, 5] и рассчитанных по моделям (1)-(4) данных кинематической вязкости кадмия,

n ×10⁷, м²/с

T	ν(эксп)	ν(1)	ν(2)	ν(3)	a	ν(4)
Tm =594	-	1,395	1,402	1,416	-	1,412
603	1,374	1,374	1,374	1,374	-	1,374
673	1,103	1,231	1,199	1,111	2,000	1,128
873	0,762	0,949	0,915	0,700	1,593	0,707
Tb=1039	-	0,797	0,790	0,527	-	0,517

T, K

T_b

T_m

n×10⁷, м²/с

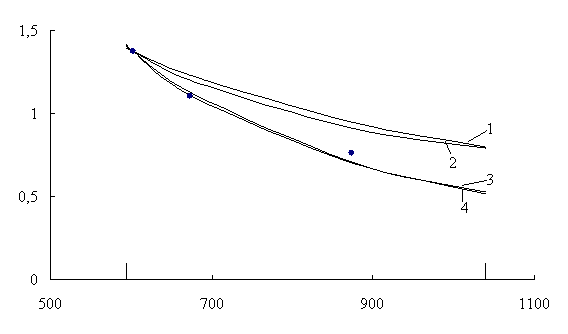
n - кинематическая вязкость, Т – температура.

Точки – экспериментальные данные [5],

1 – по модели (1), 2 – по (2), 3 – по (3), 4 – по (4)

Рисунок 1 – Зависимость кинематической вязкости кадмия от температуры

В качестве реперной взята точка с данными T_r = 603 К и n_r = 1,374×10^-7 м²/с. Здесь четко видно преимущество моделей (3) и (4). Коэффициенты корреляции соответственно равны 0,979 и 0,980. Коэффициент корреляции для усовершенствованной модели выше, поэтому для расчета вязкости можно применить модель более общего вида (4).

Среднее значение ā = 1,80 указывает на то, что в расплаве существует возможность формирования молекулярных ковалентных связей. Однородность полученного множества для а по критерию Налимова соблюдается: S(x) = 1,606; = 1,179 < r_cr = 1,483. Таким образом, с учетом степени ассоциированности кластеров в качестве обобщенной модели вязкости расплавов можно использовать модель (4). Расчетная формула для кинематической вязкости кадмия примет вид

м²/с. (8)

В указанном интервале температур для экспериментальных данных энергия активации Дж/моль, а для предлагаемой модели – Дж/моль. Зависимость логарифма вязкости кадмия от обратной температуры представлена на рисунке 2.

10⁴/T

lnν

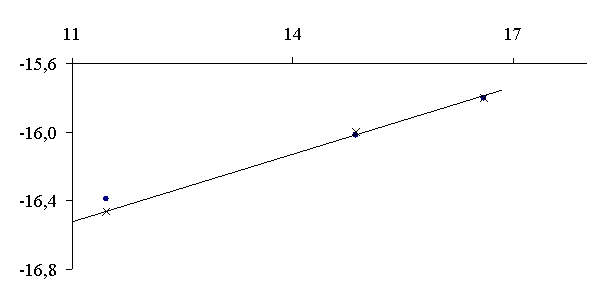n - кинематическая вязкость, Т – температура.

Точки – экспериментальные данные,

крестики – для модели (8), прямая – по уравнению

Рисунок 2 – Зависимость логарифма кинематической вязкости кадмия от обратной температур

Предлагаемая модель была проверена на 28 металлах, по которым имеются экспериментальные значения вязкости [6]. Во всех случаях предлагаемая модель описывает температурную зависимость наилучшим образом, о чем свидетельствуют полученные высокие коэффициенты корреляции.

Выводы:

1. Таким образом, для вязкости на основе концепции хаотизированных частиц создается возможность определить с удовлетворительной точностью температурную зависимость этой важнейшей характеристики в полном диапазоне жидкого состояния по единой модели, учитывающей степень ассоциации элементарных кластеров из динамически существующих кристаллоподвижных частиц.

2. Если в расплаве существуют неустойчивые зародыши твердой фазы – кластеры, состоящие из комплекса кристаллоподвижных частиц, то именно они должны препятствовать жидкотекучести металлов. Тем самым кластеры могут определять вязкость жидкости и ее зависимость от температуры. На этом основании выведена новая полуэмпирическая обобщенная модель вязкости жидких металлов в зависимости от температуры с учетом не только образования кластеров, но и степени их ассоциированности, т.е. с усилением роли кристаллоподвижных частиц.

3. Полученные данные по вязкости жидких металлов будут гарантировать практическое осуществление процессов, рассчитанных с использованием этих значений при очень высоких температурах, в более надежных оптимальных условиях.

Список использованных источников

1. Шпильрайн Э.Э., Фомин В.А., Сковородько С.Н., Сокол Т.Ф. Исследование вязкости жидких металлов. – М.: Наука, 1983. – 244 с.

2. Малышев В.П., Турдукожаева А.М., Кажикенова А.Ш. Вязкость расплавов металлов по концепции хаотизированных частиц // Тяжелое машиностроение. – 2009. – № 6. – С. 37-39.

3. Авелиани М. И., Каплун А. Б. Вязкость жидких висмута, кадмия и меди // Изв. СО АН СССР. Техн. науки, 1973. – Вып. 1. – С. 139-142.

4. Соловьев А. Н., Каплун А. Б. Исследование вязкости расплавленных металлов вибрационным методом. В кн.: Физико-механические и теплофизические свойства металлов. – М.: Наука, 1976. – 214 с.

5. Свойства элементов: Справ. изд. – В 2 кн. Кн. 1 // Под ред. Дрица М. Е. – 3-е изд., перераб. и доп. – М.: Изд. дом «Руда и Металлы», 2003. – С.448.

6. Кажикенова А.Ш. Разработка обобщенной полуэмпирической модели вязкости жидких металлов на основе концепции хаотизированных частиц с учетом степени ассоциированности кластеров: автореф. дисс. … канд. техн. наук: 05.16.08. – Караганда: КарГУ им. Е.А.Букетова, 2010. – 21 с.