Куракбаев Д.С, Самбетова Р.А., Ибрагимов У.М.

Южно-Казахстанский государственный университет им. М.Ауезова, Шымкент, Казахстан

об Одном алгоритме решения задачи избежания столкновений фазовой точки в управляемой системе

Пусть дана управляемая система [1]

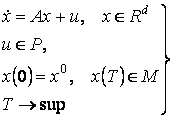(1)

где –фазовый вектор, –вектор управления, принимающий свои значения из области , являющаяся компактным подмножеством .

Для формулировки принципа максимума мы рассмотрим еще одну систему уравнений относительно допольнительных переменных

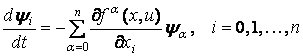. (2)

Вводя -мерный вектор и функцию Понтрягина

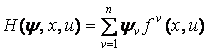, (3)

мы можем записать уравнения (1) в виде

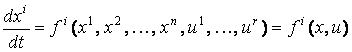, (4)

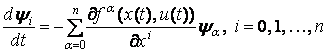и (5)

в виде гамильтоновой системы

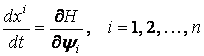, (6)

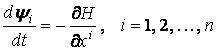. (7)

Теорема [2]. Пусть , - такое допустимое управление, переводящее фазовую точку из положения в положение , a - соответствующая траектория, так что . Для оптимальности управления и траектории необходимо существование такой ненулевой непрерывной вектор-функции , соответствующей функциями и , что:

1⁰. для всех , функция переменного достигает в точке максимума

; (8)

2⁰. в конечный момент выполнено соотношение

. (9)

Пример [3]. Пусть - тело (материальная точка), которое может совершать прямолинейное движение (рис.1). Массу этого тела будем предполагать постоянной и равной , а его размерами будем пренебрегать. Координату тела будемь обозначать через . При движении тела его координата меняется с течением времени. Производная представляет собой скорость движения тела . Будем предполагать, что на тело действуют две внешние силы: сила трения и упругая сила , кроме того тело снабжено двигателем.

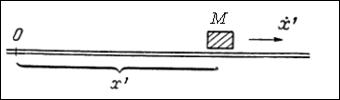
Рис. 1 – Движение тела (материальной точки)

Развиваемую двигателем силу воздействия на тело обозначим через . Таким образом, по второму закону Ньютона движение тела с течением времени будет описывать дифференциальным уравнением

(10)

Обозначив скорость движения через , мы сможем записать закон движения в виде следующей системы дифференциальных уравнений:

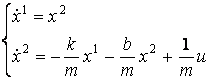(11)

Далее, рассмотрим случай, когда сила трения и упругая сила отсутствуют (, ), масса равна единице (), а управляющий параметр подчинен ограничениям . Иначе говоря, мы рассматриваем материальную точку массы , свободно и без трения движущуюся по горизонтальной прямой и снабженную двигателем, развивающим силу , где .

Согласно (11) уравнения движения тела имеют вид

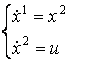(12)

Функция в рассматриваемом случае имеет вид

, (13)

а матрица записывается в виде

.

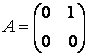Далее, для вспомогательных переменных мы получаем систему уравнений

,

откуда ( - постоянные). Соотношение (8) дает нам (учитывая (13) и условие )

. (14)

Из (14) следует, что каждое оптимальное управление , являются кусочно-постоянной функцией, принимающей значения и имеющей не более двух интервалов постоянства (ибо линейная функция не более одного раза меняет знак на отрезке ).

Для отрезка времени, на котором , мы имеем (в силу системы (12))

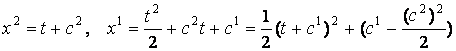
( - постоянные интегрирования), откуда получаем

, (15)

где - постоянная. Таким образом, фазовые траектории, для которого , представляет собой дугу параболы.

Аналогично, для отрезка времени, на котором , мы имеем

,

,

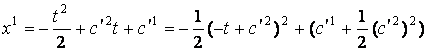откуда получаем

. (16)

На следующей рисунке (рис.2) изображено все полученные таким образом фазовые траектории (-траектория уравнения (15), расположенная в нижней полуплоскости; -траектория уравнения (16), расположенная в верхней полуплоскости). Фазовая точка движется по проходящей через начальную точку траектории уравнеия (16), если точка расположена выше линии и по траектории уравнения (15), если точка расположена ниже этой линии. Иначе говоря, если начальное положение расположено выше траектории , то фазовая точка должна двигаться под воздействием управления до тех пор, пока она не попадет на траекторию ; в момент попадания на траекторию значение управления переключается и становится равным +1 вплоть до момента попадания в начало координат. Если же начальное положение расположено ниже траектории , то управление должно быть равно +1 до момента попадания на траекторию , а в момент попадания на траекторию значение управление переключается и становится равным -1.

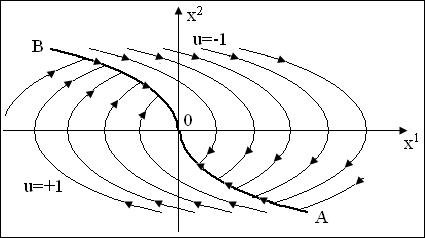
Рис. 2 – Оптимальные траектории уравнения (12)

Таким образом, найденные траектории являются оптимальными, и других оптимальных траекторий, ведущих в начало координат, не существует.

Литература

1. Куракбаев Д.С. Ибрагимов У.М. Численное моделирование задачи живучести в управляемых системах // LAP LAMBERT Academic Publishing. Germany, 2012. -72 c.

2. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. –М.: Наука, 1969. -384 с.

3. Болтянский В.Г. Математические методы оптимального управления. –М.: Наука, 1968. -408 с.