К.ф.-м.н Сейтханова А.К

Инновационный Евразийский университет, Казахстан, г.Павлодар

О построении матрицы коэффициентов отражения и преломления связанных упругих и термоупругих волн

Связанная система уравнений движения и уравнения теплопроводности описывающая распространения термоупругих волн на основе метода матрицанта может быть приведена к системе обыкновенных дифференциальных уравнений (в случае неоднородности вдоль оси z):

; ;

- вектор-столбец граничных условий;

- компоненты вектора смещения;

- компоненты тензора напряжений;

- приведенная температура среды;

- компонента вектора теплового потока.

Матрица В является матрицей коэффициентов, содержащая в себе упругие и термомеханические параметры среды.

В данной статье рассматривается отражение упругой волны от термоупругого полупространства. Плоскость контакта определяется координатой z=0.

В случае плоских гармонических волн граничные условия для определения полей отраженных, преломленных волн имеют вид:

(1)

(2)

Здесь - поле заданных падающих волн на границе z=0 из области z<0.

Область z>0 является термоупругой средой. - поле отраженных волн. - поле преломленных волн. Область z<0 – упругая изотропная среда.

Формальное решение системы уравнении (1) и (2) имеет вид:

Вычисление матриц R₀, R_t .

Рассмотрим одномерное распространение термоупругих волн с матрицей коэффициентов B термоупругой среды в виде

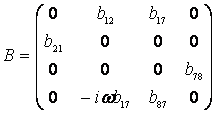
Получено выражение для матрицы R.

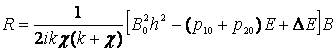(3)

где

; , (4)

Вычисления на основе (3), с учетом выражений (4) позволяют получить явный вид матрицы R_t:

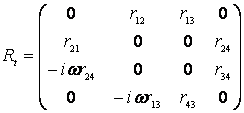(5)

Элементы матрицы R_t получены в виде:

, , , , ,

, , , ,

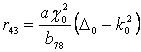Матрица коэффициентов B упругих и тепловых волн в анизотропной среде имеет вид:

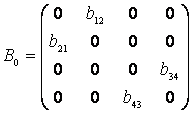(6)

, , ,

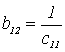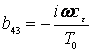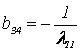
Матрица R₀ имеет вид:

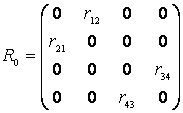(7)

Элементы матрицы R₀ получены в виде:

, , ,

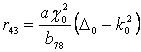
следует: , , .

Обратная матрица определена в виде:

(8)

Литература:

1. Новацкий В. Теория упругости. - М.: «Мир», 1986, 556 с.

2. Тлеукенов С.К., Кудерин М.К., Козионов В.А., Испулов Н.А., Баяубаев Е.К., Сейтханова А.К. Динамические и термодинамические процессы в скальных грунтах и строительных конструкциях. Монография под ред. академика АЕН, д.ф.-м.н., профессора С.К. Тлеукенова. - Павлодар, 2006 г.

3. С.К. Тлеукенов, М.Н. Ильясов, К.Р. Досумбеков, О матричной формулировке задачи отражения и преломления термоупругих волн // Материалы международной научной конференции «Вторые Ержановские чтения», г. Актобе, 2007 г.

4. Сейтханова А.К. О задаче отражения – преломления упругой волны на границе термоупругого полупространства // Вестник ПГУ. Серия Физико-математическая, № 4, Павлодар, НИЦ ПГУ им. С. Торайгырова, 2010 г.