Математика/4. Прикладная математика

К.ф.-м.н. Зинченко А.Б., Колотушкина Д.М.

Южный федеральный университет. Россия

Новое компромиссное значение кооперативной ТП-игры

Классическая кооперативная игра , где , , , , имеет экспоненциальную (относительно числа агентов ) длину входа, т.к. . Если в игре много участников, то нахождение решения, зависящего от всех (или почти всех) значений характеристической функции , - сложная вычислительная задача. Однако существуют классы игр, в которых трудно вычисляемые в общем случае решения находятся за полиномиальное (относительно ) время.

Приведем несколько примеров:

· в формуле для N-ядра и τ-значения игры большого босса [1]

используются только значений функции ;

· для нахождения элемента С-ядра производственной игры [2] достаточно решить линейную задачу с числом переменных, равным количеству видов продукции, и числом ограничений, равным количеству типов ресурсов;

· τ-значение выпуклой игры определяется системой, содержащей значений функции ;

· -значения игры с непустыми множествами дележей и двойственных дележей определяются формулами

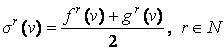, (1)

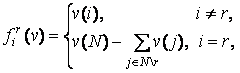
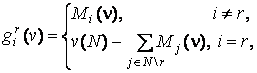(2)

, , содержащими значений функции .

Выпуклые игры, игры большого босса и другие классы игр, для которых существуют эффективные алгоритмы вычисления основных решений, составляют небольшую часть множества всех игр . Решения, которые вычисляются просто (-значения, СС-ядро и др.) часто не соответствуют интуитивному понятию справедливости.

В данной работе вводится новое одноточечное решение (-центр ) игры , являющиеся средним арифметическим -значений , ,

.

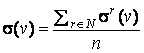Исследуются свойства . Имея ту же оценку сложности , что и -значения, -центр, как правило, более приемлем для конкретных игр, чем любое из -значений. Кроме того, -центр, как и -значения, определен на достаточно широком подмножестве игр , удовлетворяющих условию

. (3)

Пусть - множество всех характеристических функций , . Подмножество функций , удовлетворяющих (3), обозначим через . Подставив (2) в (1), получаем

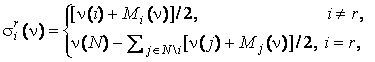(4)

для всех . Покажем, что удовлетворяет трем из четырех аксиом, характеризующим значение Шепли. Пусть - множество значений игры , где , а - множество значений игры , где .

Аксиома 1 (эффективность): для всех .

Аксиома 2 (симметричность): для всех , , если и симметричные игроки.

Аксиома 3 (аддитивность): для любых , ,

где , .

Теорема 1. В классе , -центр удовлетворяет аксиомам эффективности, симметричности, и аддитивности.

Доказательство. Используя (4), получаем следующую формулу для -центра: , где

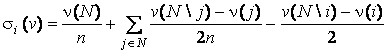. (5)

Суммируя , имеем

.

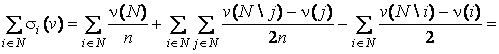
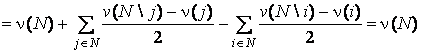Значит, удовлетворяет аксиоме эффективности.

Если игроки симметричны, т.е. , , то и для -элементных коалиций , , имеем . Следовательно, . Доказано, что удовлетворяет аксиоме симметричности.

Пусть . Из соотношений

,

вытекает , т.е. . Кроме того,

, .

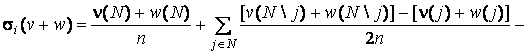
Из и следует, что -центр удовлетворяет аксиоме аддитивности. š

Для аксиоматического обоснования -центра введем новую аксиому, определяющую выигрыш нулевого игрока.

Аксиома 4 (модифицированное свойство нулевого игрока). Для любой функции , если - нулевой игрок в , то

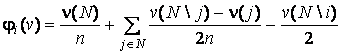. (6)

Теорема 2. В классе , существует единственное значение , удовлетворяющее аксиомам 1 - 4. Оно совпадает с -центром игры .

Доказательство. Если - нулевой игрок в , то подставив в (5), получаем (6). Значит, удовлетворяет аксиоме 4, а также, согласно теореме 1, аксиомам 1 - 3. Докажем, что эти аксиомы определяют единственное значение игры , где , , - игра единогласия: для , для .Из сбалансированности игры следует, что .

Рассмотрим три случая.

1. . Игра симметричная. По аксиоме 2, , .

2. для некоторого . Тогда , , , для . Все игроки коалиции нулевые в . Согласно аксиоме 4, , . По аксиоме эффективности .

3.. Тогда для всех , для , для . Все игроки коалиции нулевые в . По аксиоме 4, , .

По аксиоме 1,

.

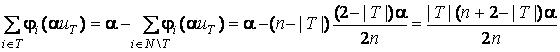Все игроки коалиции попарно симметричны. По аксиоме 2,

, .

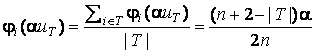Доказано, что однозначно определено аксиомами 1 – 4. Единственность для любой функции следует из аксиомы аддитивности и из того, что семейство функций , , образует базис в . •

Пример 1. В парламенте 60 мест. Большая партия (большой игрок) имеет 30 мест, три малые партии (малые игроки) - по 10 мест каждая. Решение принимается простым большинством голосов. Это игра голосования с множеством минимальных выигрывающих коалиций =. Единственный дележ С-ядра, совпадающий с N-ядром, называют в литературе по кооперативным играм контр-интуитивным и даже тираническим. Согласно значению Шепли большой игрок получает 3/4 выигрыша максимальной коалиции, а остаток - равномерно распределяется между малыми игроками. В -центре выигрыши малых игроков увеличиваются. Нетрудно проверить, что доминирует по Лоренсу и .

Пример 2. В парламенте 40 мест. Большая партия имеет 20 мест, две малые партии - по 10 мест, т.е. имеем игру , где =. С-ядро состоит из одного дележа . В этой игре -центр совпадает с значением Шепли и доминирует по Лоренсу .

Литература:

1. Muto S., Nakayama M., Potters J., Tijs S. On big boss games // The Economic Studies Quarterly. 1988. Vol. 39. No. 4. P. 303-321.

2. Owen G. On the core of linear production games // Math. Programming. 1975. Vol. 9. P. 358-370.