К.п.н. Алексеева Е.Е.

Балтийская государственная академия рыбопромыслового флота, Калининград, Россия

РАЗЛОЖЕНИЕ В СТЕПЕННОЙ РЯД ЛОГАРИФМИЧЕСКИХ ФУНКЦИЙ

Для получения разложения в ряд логарифмической функции воспользуемся функцией гиперболы и её разложением в ряд:

(1)

Интегрируя обе части равенства (1) в пределах от 0 до получим:

(2)

Другая форма записи уравнения гиперболы и её разложения в ряд имеет вид:

Интегрирование этого разложения в тех же пределах даёт логарифмическое разложение вида:

(3)

Разложение (3), как и разложение (2) сходится на единичном отрезке, хотя сами функции существуют и за пределами этого отрезка. Здесь так же, как и с биномом Ньютона встаёт вопрос о получении ряда-эквивалента, воспроизводящего исходную функцию за пределами единичного отрезка. Отыскание ряда-эквивалента в данном случае можно осуществить, применяя композиционный метод. Подставляя в выражение (3) вместо x обратную величину 1/x, получим:

(4)

Значение в правой части выражения (4) можно в свою очередь разложить в ряд, например:

(5)

Окончательно выражение (4) с учётом (5) перепишется к виду:

Таким образом, полное разложение в ряд функции во всей области её существования записывается в виде:

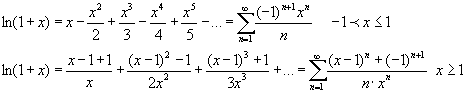(6)

Подобным образом может быть получено разложение в ряд любой логарифмической функции во всей области её существования.

Композиционный метод получения разложений в ряд логарифмических функций

Разложение функции в ряд представляется в виде равенства этой функции и ряда. Если аргументом функции и соответствующего ей функционального ряда является действительное число, то аргумент и в функции и в ряде можно заменить произвольной функцией при единственном условии, что функция во всей области определения выражается действительным числом. В сути этого положения лежит принцип суперпозиции, а такой метод образования новых функций и их разложений в ряд называется композиционным.

Композиционный метод позволяет получить из одного выражения бесконечное множество других выражений с другими характеристиками.

Так, например, заменяя по правилу суперпозиции в выражении (2) величину величиной , получим:

(7)

Замена в выражении (7) величины аргумента на величину даёт:

(8)

Любому действительному числу , кроме нуля, можно однозначно поставить в соответствие его обратную величину . В связи с этим по правилу суперпозиции имеем право в выражении (7) заменить значение аргумента величиной ему обратной , после чего получим:

(9)

Заменив в выражении (8) аргумент на обратную величину , получим формулу разложения:

(10)

Как видно, композиционный метод преобразования логарифмических разложений позволяет получать самые разнообразные логарифмические разложения в ряд.

Другие разложения в ряд логарифмических функций, полученных таким образом, к примеру, имеют вид:

(11)

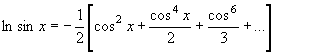
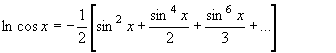
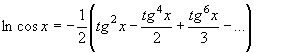
Почленное вычитание логарифмических рядов позволяет переходить к другим видам функций и их разложений. К примеру, вычитая почленно из равенства (3) равенство (2), получим:

(12)

Произведя операцию замены в выражении (12) значения аргумента на значение получим:

(13)

Метод композиции применительно к разложениям в ряд логарифмических функций позволяет достаточно быстро и эффективно находить новые решения, но следует напомнить, что для каждого нового найденного разложения радиус сходимости ряда должен находиться заново.

Повышение сходимости логарифмических рядов и увеличение их радиуса сходимости

При практических вычислениях логарифмов, как в компьютерных вычислениях, так и в приближённых аналитических расчётах представляют повышенный интерес разложения в ряд с высокой сходимостью и большим радиусом сходимости. Решение этой задачи выполняется весьма эффективно с использованием того же самого композиционного метода.

Покажем это на примере логарифмического разложения (4), которое, имеет единичный радиус сходимости:

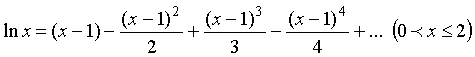(14)

На основании принципа суперпозиции заменим в этом выражении аргумент функцией имеющей вид , после чего оно перепишется к виду:

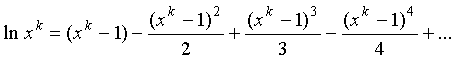(15)

Этот новый ряд можно переписать к виду:

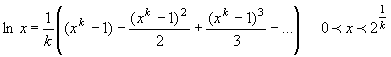(16)

Из выражения (16) видно, что для увеличения радиуса сходимости ряда показатель степени следует выбирать меньше единицы.

К примеру, если , то ряд перепишется к виду:

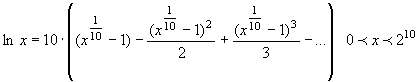(17)

Из сравнения выражений (14) и (17) видно, что радиус сходимости в данном случае увеличился в 512 раз.

Для вычисления значения с точностью до третьей значащей цифры в выражении (14) необходимо просуммировать 304 слагаемых, а в выражении (17) достаточно только 2 слагаемых. Это обстоятельство представляется особо ценным фактом в вопросах аналитической аппроксимации логарифмических функций с использованием рядов.

По выражению (14) можно считать логарифмы только от нуля до двух, а по выражению (17) от нуля до 1024. Очевидно, что такие преимущества достаются ценой необходимости вычисления корня десятой степени из аргумента .