Акишев Г., Мырзагалиева А.Х.
Карагандинский государственный
университет им. Е.А. Букетова, Караганда
ОЦЕНКИ НАИЛУЧШЕГО
ОРТОГОНАЛЬНОГО ПРИБЛИЖЕНИЯ КЛАССА НИКОЛЬСКОГО-БЕСОВА
Пусть 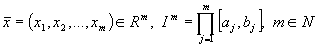 . Через
. Через 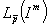 обозначим пространство измеримых по Лебегу
функций
обозначим пространство измеримых по Лебегу
функций 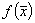 , для которых (см. [1])
, для которых (см. [1])
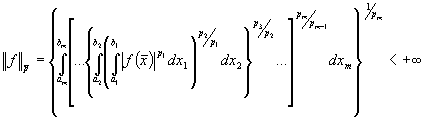 ,
,
где 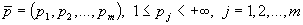 .
.
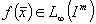 , если
, если 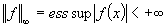 (см. [1]).
(см. [1]).
Определение 1 (см. [2]).
Система функций 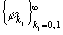 обладает B-свойством, если существует такое
обладает B-свойством, если существует такое 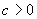 , что 1) каждый полином
, что 1) каждый полином 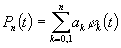 по этой системе непрерывен
и кусочно-дифференцируем, при этом длина интервалов дифференцируемости больше
или равно
по этой системе непрерывен
и кусочно-дифференцируем, при этом длина интервалов дифференцируемости больше
или равно 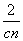 ; 2) для него выполняется неравенство типа Бернштейна:
; 2) для него выполняется неравенство типа Бернштейна: 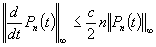 .
.
Определение
2 (см.
[2]). Система функций 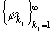 обладает R-свойством, если полином
обладает R-свойством, если полином 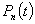 по этой системе
кусочно-постоянен и длина интервалов постоянства не меньше, чем
по этой системе
кусочно-постоянен и длина интервалов постоянства не меньше, чем 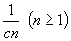 , где
, где 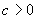 - константа,
зависящая лишь от системы.
- константа,
зависящая лишь от системы.
Замечание. В качестве примеров
систем, обладающих В-свойством, укажем тригонометрическую систему, а также
системы сплайн-функций, изучавшиеся в работах Чисельского и его учеников, в
частности, системы Франклина 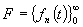 и Чисельского
и Чисельского 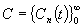 . Примерами систем, обладающих R-свойством,
могут служить системы Уолша, Хаара и их обобщения – периодические мультипликативные
системы Виленкина и связанные с ними так называемые системы сходимости – при
ограниченных в совокупности образующих числах
. Примерами систем, обладающих R-свойством,
могут служить системы Уолша, Хаара и их обобщения – периодические мультипликативные
системы Виленкина и связанные с ними так называемые системы сходимости – при
ограниченных в совокупности образующих числах 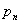 .
.
Рассмотрим на каждом отрезке 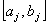 ортонормированную
систему функций
ортонормированную
систему функций 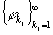 , удовлетворяющую
, удовлетворяющую 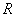 или
или 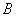 - условиям. Через
- условиям. Через 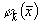 обозначим декартовое
произведение этой функции
обозначим декартовое
произведение этой функции 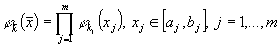 .
.
Пусть 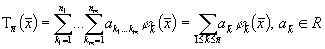 полином по данной
системе. Любой полином по данной ортонормированной системе функций можно
представить в виде
полином по данной
системе. Любой полином по данной ортонормированной системе функций можно
представить в виде
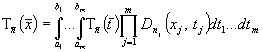 , (1)
, (1)
где 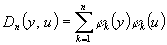 - ядро Дирихле.
- ядро Дирихле.
Пусть 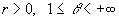 ,
, 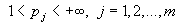 . Пространством Бесова
. Пространством Бесова 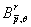 называется множество функций
называется множество функций
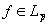 , для которых
, для которых
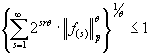 ,
,
где 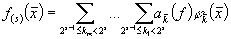 , если же
, если же 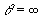 , то
, то 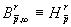 - класс Никольского.
- класс Никольского.
Пусть 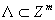 некоторое конечное множество.
Количество его элементов обозначим через
некоторое конечное множество.
Количество его элементов обозначим через 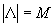 . Для заданной функции
. Для заданной функции 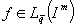 положим
положим
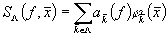 .
.
Наилучшим
ортогональным приближением называется (см. [3])
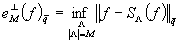 .
.
Для заданного класса 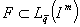 положим
положим
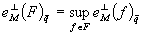 .
.
Оценки
этой величины для различных классов исследовали В.Н. Темляков [3], Э.С.
Белинский [4], А.С. Романюк [5], [6].
Через 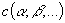 будем обозначать
положительные величины, зависящие от указанных в скобках параметров, различные
в разных формулах.
будем обозначать
положительные величины, зависящие от указанных в скобках параметров, различные
в разных формулах.
Для
краткости будем пользоваться записью 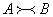 , которая означает, что существуют положительные постоянные
, которая означает, что существуют положительные постоянные 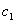 и
и 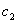 такие, что
такие, что 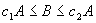 .
.
Задача данной работы заключается в
нахождении порядка величины 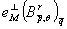 для
для 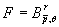 . Для этого сначала докажем неравенство Джексона -
Никольского, которое будет использоваться при доказательстве основного
результата.
. Для этого сначала докажем неравенство Джексона -
Никольского, которое будет использоваться при доказательстве основного
результата.
Теорема
1 .
Пусть 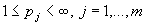 и система функций
и система функций 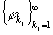 удовлетворяет
удовлетворяет 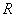 или
или 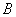 условиям. Тогда для
любого кратного полинома по этой системе имеет место неравенство
условиям. Тогда для
любого кратного полинома по этой системе имеет место неравенство
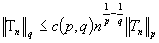 .
.
Доказательство. Пусть 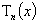 произвольный полином
по системе функций
произвольный полином
по системе функций 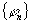 . Из формулы (1) при
. Из формулы (1) при 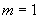 следует
следует
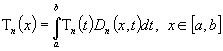 . (4)
. (4)
Представим
в (4) выражение под интегралом в виде
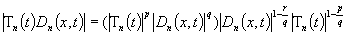
и применим для
оценки интеграла неравенство Гельдера для трех функций (см. [1]) при 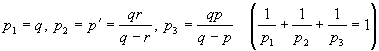 . Тогда
. Тогда
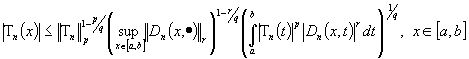 .
.
Теперь
обе части возведем в степень 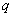 и проинтегрируем,
применяя теорему Фубини (см. [7]) для интеграла и,
возводя в степень
и проинтегрируем,
применяя теорему Фубини (см. [7]) для интеграла и,
возводя в степень 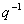 , находим
, находим
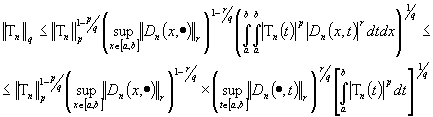
Отсюда 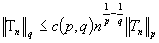 . Теорема доказана.
. Теорема доказана.
Замечание. Теорема 2 была доказана в
работе Комисарова А.А. (см. [2]), выше же был приведен иной способ
доказательства.
Теорема 3. Пусть 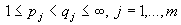 и система
и система 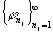 удовлетворяет
удовлетворяет 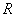 или
или 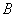 условиям. Тогда для
любого полинома по этой системе имеет место неравенство
условиям. Тогда для
любого полинома по этой системе имеет место неравенство
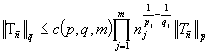 .
.
Доказательство. Используем метод
математической индукции. Пусть 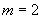 , тогда
, тогда
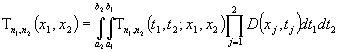 .
.
Для оценки интеграла применим теорему 2
при фиксированном 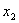 , т.е.
, т.е.
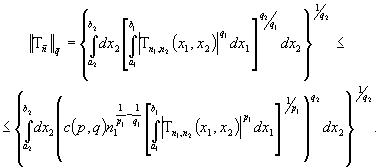 (5)
(5)
Известно, что 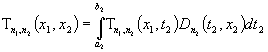 . Данное равенство ставим во внутренний интеграл выражения
(5) при фиксированном
. Данное равенство ставим во внутренний интеграл выражения
(5) при фиксированном 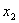 , после применяем обобщенное неравенство Минковского (см.
[1]). В итоге получаем
, после применяем обобщенное неравенство Минковского (см.
[1]). В итоге получаем
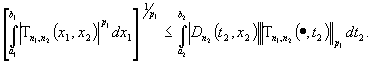 (6)
(6)
Из (5) и (6) следует
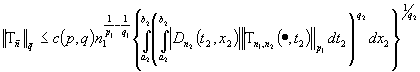 . (7)
. (7)
В неравенстве (7) обозначим через 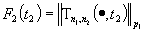 , соответственно получим
, соответственно получим
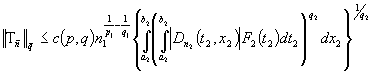 .
.
Теперь
повторяя всю процедуру доказательства теоремы 2, получим
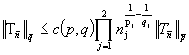 , где
, где 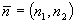 .
.
Пусть неравенство верно при 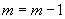 , т.е.
, т.е.
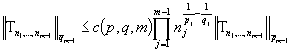 , (8)
, (8)
где 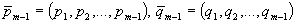 .
.
Теперь докажем для 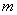 . Пользуясь предположением (8), имеем
. Пользуясь предположением (8), имеем
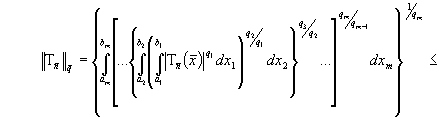
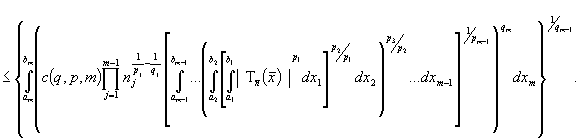 (9)
(9)
Формулу 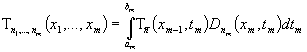 ставим во внутренний
интеграл в неравенстве (9) при фиксированном
ставим во внутренний
интеграл в неравенстве (9) при фиксированном 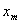 , после этого применяем обобщенное неравенство Минковского
(см.[1]) и в итоге получаем
, после этого применяем обобщенное неравенство Минковского
(см.[1]) и в итоге получаем
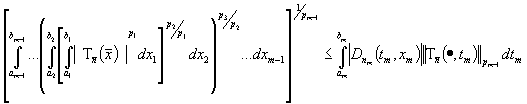 . (10)
. (10)
Из (9), (10) следует
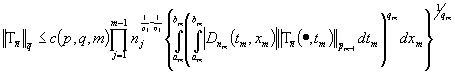 .
.
Обозначим через 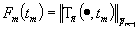 , тогда получим
, тогда получим
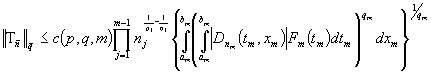 .
.
Снова повторяя процедуру доказательства
теоремы
2, получим
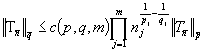 .
.
Теорема доказана.
Замечание. В частности из теорем 1 и
3 следуют известные неравенства Джексона – Никольского для полиномов по
тригонометрической системе и системам Уолша, Хаара [8].
Теорема 4. Пусть 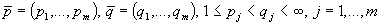 ,
,
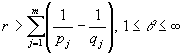 и система
и система 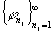 удовлетворяет
удовлетворяет 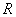 или
или 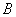 условиям. Тогда
условиям. Тогда
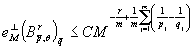 ,
,
где 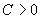 постоянная,
независящая от
постоянная,
независящая от 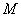 .
.
Доказательство.
Известно, что 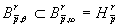 , то оценку достаточно доказать для
, то оценку достаточно доказать для 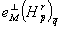 .
.
Пусть
функция 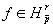 . Для
. Для 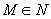 выберем число
выберем число 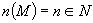 так, чтобы
так, чтобы 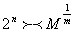 . Также для функции
. Также для функции 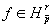 рассмотрим кубическую
частичную сумму
рассмотрим кубическую
частичную сумму 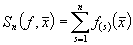 . Тогда, применяя теорему 3, получим
. Тогда, применяя теорему 3, получим
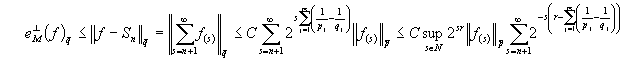 .
.
Так как 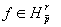 и
и 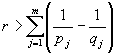 , то
, то 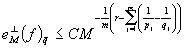 .
.
Следовательно, 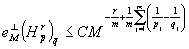 .
.
Так как 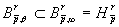 , то
, то 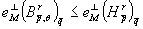 . Поэтому из доказанного неравенства следует, что
. Поэтому из доказанного неравенства следует, что 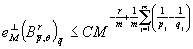 . Теорема доказана.
. Теорема доказана.
Замечание. Точность утверждения
теоремы 4 доказана для системы Уолша и тригонометрической системы. При 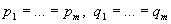 утверждение теоремы 4 для тригонометрической системы
доказал А. С. Романюк [6].
утверждение теоремы 4 для тригонометрической системы
доказал А. С. Романюк [6].
Литература:
1.
Бесов
О.В., Ильин В.П., Никольский С.М. Интегральные представления функций и теоремы
вложения. − М.: Наука, 1975. − 480 с.
2.
Комиссаров
А.А. О некоторых свойствах функциональных систем// Деп. в ВИНИТИ. – М.: – 1983.
- №5827-83. – С.28.
3.
Темляков
В.Н. О приближении периодических функций нескольких переменных // Докл. АН
СССР. – 1984. – Т. 279. - № 2. – С. 301 – 305.
4.
Белинский
Э.С. Приближение плавающей системой экспонент на классах периодических функций
с ограниченной смешанной производной// Исследования по теории функций многих
вещественных переменных. Ярославль: ЯГУ, 1988. С. 16-33.
5.
Романюк
А.С. Приближение классов периодических функций многих переменных// Мат.
заметки. – 2002. – Т. 71. – Выпуск 1. – С. 109-121.
6.
Romanyuk A.S. Approximative
characteristics of the isotropic classes of periodic functions of many
variables// Ukrain. Math.
Journal. – 2009. –
Vol. 61. - № 4. – P. 613 – 626.
7.
Колмогоров
А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.:
Наука, 1976 г.
8.
Голубов
Б.И., Ефимов А.В., Скворцов В.А. Ряды и преобразования Уолша. − М.:
Наука, 1987. − 344 с.
![]() . Через
. Через ![]() обозначим пространство измеримых по Лебегу
функций
обозначим пространство измеримых по Лебегу
функций ![]() , для которых (см. [1])
, для которых (см. [1])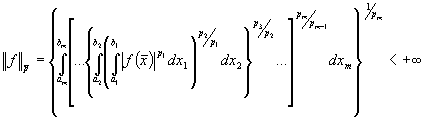 ,
,![]() .
.![]() , если
, если ![]() (см. [1]).
(см. [1]).![]() обладает B-свойством, если существует такое
обладает B-свойством, если существует такое ![]() , что 1) каждый полином
, что 1) каждый полином ![]() по этой системе непрерывен
и кусочно-дифференцируем, при этом длина интервалов дифференцируемости больше
или равно
по этой системе непрерывен
и кусочно-дифференцируем, при этом длина интервалов дифференцируемости больше
или равно ![]() ; 2) для него выполняется неравенство типа Бернштейна:
; 2) для него выполняется неравенство типа Бернштейна: ![]() .
.![]() обладает R-свойством, если полином
обладает R-свойством, если полином ![]() по этой системе
кусочно-постоянен и длина интервалов постоянства не меньше, чем
по этой системе
кусочно-постоянен и длина интервалов постоянства не меньше, чем ![]() , где
, где ![]() - константа,
зависящая лишь от системы.
- константа,
зависящая лишь от системы.![]() и Чисельского
и Чисельского ![]() . Примерами систем, обладающих R-свойством,
могут служить системы Уолша, Хаара и их обобщения – периодические мультипликативные
системы Виленкина и связанные с ними так называемые системы сходимости – при
ограниченных в совокупности образующих числах
. Примерами систем, обладающих R-свойством,
могут служить системы Уолша, Хаара и их обобщения – периодические мультипликативные
системы Виленкина и связанные с ними так называемые системы сходимости – при
ограниченных в совокупности образующих числах ![]() .
.![]() ортонормированную
систему функций
ортонормированную
систему функций ![]() , удовлетворяющую
, удовлетворяющую ![]() или
или ![]() - условиям. Через
- условиям. Через ![]() обозначим декартовое
произведение этой функции
обозначим декартовое
произведение этой функции ![]() .
.![]() полином по данной
системе. Любой полином по данной ортонормированной системе функций можно
представить в виде
полином по данной
системе. Любой полином по данной ортонормированной системе функций можно
представить в виде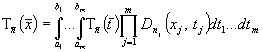 , (1)
, (1)![]() - ядро Дирихле.
- ядро Дирихле.![]() ,
, ![]() . Пространством Бесова
. Пространством Бесова ![]() называется множество функций
называется множество функций
![]() , для которых
, для которых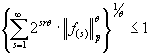 ,
,![]() , если же
, если же ![]() , то
, то ![]() - класс Никольского.
- класс Никольского.![]() некоторое конечное множество.
Количество его элементов обозначим через
некоторое конечное множество.
Количество его элементов обозначим через ![]() . Для заданной функции
. Для заданной функции ![]() положим
положим![]() .
.![]() .
.![]() положим
положим![]() .
.![]() будем обозначать
положительные величины, зависящие от указанных в скобках параметров, различные
в разных формулах.
будем обозначать
положительные величины, зависящие от указанных в скобках параметров, различные
в разных формулах.![]() , которая означает, что существуют положительные постоянные
, которая означает, что существуют положительные постоянные ![]() и
и ![]() такие, что
такие, что ![]() .
.![]() для
для ![]() . Для этого сначала докажем неравенство Джексона -
Никольского, которое будет использоваться при доказательстве основного
результата.
. Для этого сначала докажем неравенство Джексона -
Никольского, которое будет использоваться при доказательстве основного
результата.![]() и система функций
и система функций ![]() удовлетворяет
удовлетворяет ![]() или
или ![]() условиям. Тогда для
любого кратного полинома по этой системе имеет место неравенство
условиям. Тогда для
любого кратного полинома по этой системе имеет место неравенство 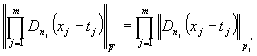 .
.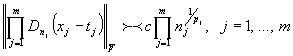 .
.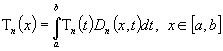 .
.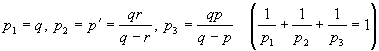 . Тогда
. Тогда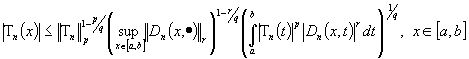 .
.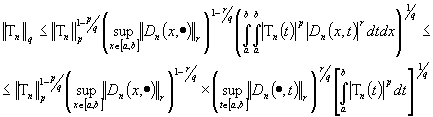
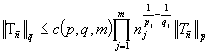 .
.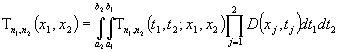 .
.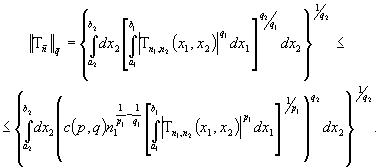
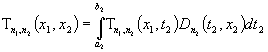 . Данное равенство ставим во внутренний интеграл выражения
(5) при фиксированном
. Данное равенство ставим во внутренний интеграл выражения
(5) при фиксированном 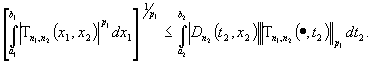
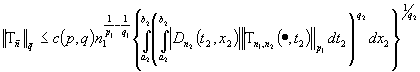 .
.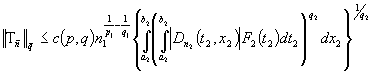 .
.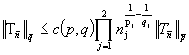 , где
, где 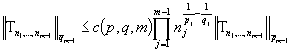 ,
,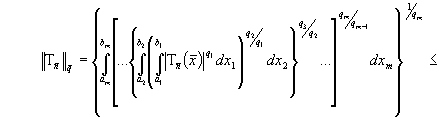
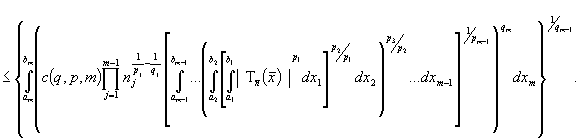
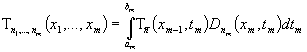
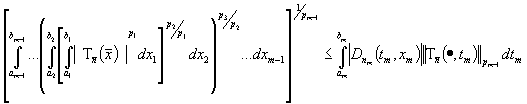 .
.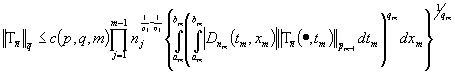 .
.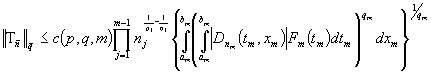 .
.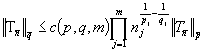 .
.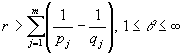
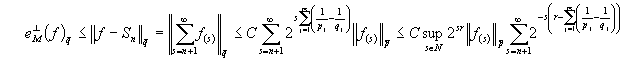 .
.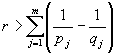 , то
, то