Количественное описание эффекта Томса в процессах транспортировки нефтяных эмульсий

Байбекова Л.Р., Шарифуллин А.В.

Казанский национальный исследовательский технологический университет

«Классическое» определение количественной оценки эффекта Томса выражается в увеличении расхода жидкости при постоянном давлении:

(1.1)

где L₀ – расход жидкости при отсутствии добавки, м³/ч;

L – расход жидкости в присутствии добавки, м³/ч.

Однако, преобразования формулы для количественной оценки величины эффекта Томса позволяют учесть, те данные, которые получены при проведении экспериментов. Так по определению давление должно быть постоянным, но после сокращений величина эффекта Томса (ВЭТ) будет рассчитываться по формуле

(1.2)

где λ и λ₀ – коэффициенты гидравлического сопротивления, которые находятся из формулы Дарси-Вейсбаха (1.3).

Формула Дарси-Вейсбаха (1.3) позволяет рассчитать перепад давления жидкости в трубопроводе диаметром d и длиной l. Здесь же используется такой параметр как коэффициент гидравлического сопротивления[5,6]

(1.3)

В таблице 1.1 представлены результаты экспериментов и расчетов величины эффекта Томса (ВЭТ) на примере полимера КМЦ найденные по двум формулам (1.1) и (1.2).

Таблица 1.1 – Результаты экспериментов и расчетов величины эффекта Томса при добавлении КМЦ

Номер экспериментальной точки	Концентрация присадки, мг/л	Расход, м^3/ч	Средняя скорость потока, м/с	Перепад давления на змеевике, кгс/см^2	Коэффициент гидравлического сопротивления	ВЭТ по формуле (1.1), %	ВЭТ по формуле (1.2), %
	0	1,263	4,469	3	0,065486
С1	2	1,28	4,529	3	0,063758	1,346	1,346
С2	6	1,33	4,706	3	0,059054	5,304	5,304
С3	8	1,33	4,706	3	0,059054	5,304	5,304
С4	10	1,316	4,656	2,8	0,056296	4,196	7,853
С5	12	1,345	4,759	3,02	0,058129	6,492	6,139
С6	15	1,342	4,748	2,9	0,056069	6,254	8,071
С7	17	1,332	4,713	2,9	0,056914	5,463	7,266
С8	20	1,33	4,706	2,9	0,057085	5,304	7,105

На основании данных таблицы 1.1 была определена графическая зависимость величины эффекта Томса (ВЭТ) от концентрации вводимого полимера, которая представлена на рис. 1.1.

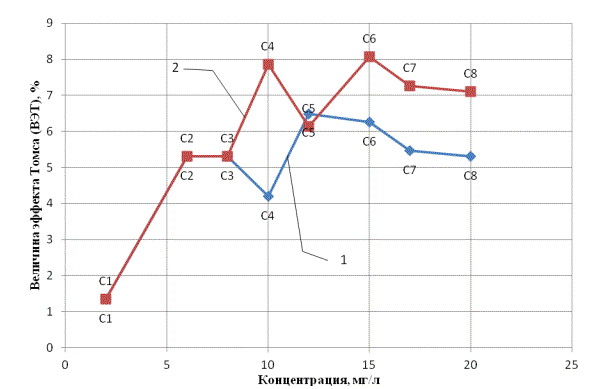
Рис. 1.1 – Сравнительная зависимость величины эффекта Томса (ВЭТ) от концентрации полимера КМЦ при t=25˚С и Re=40000÷60000: 1 – величина эффекта Томса (ВЭТ) по формуле (1.1); 2 –величина эффекта Томса (ВЭТ) по формуле (1.2)

Как видно на графике, при интерпретации эффекта Томса данными формулами, возникают некоторые различия в количественном отношении. Анализируя данную зависимость можно заметить, что различия возникают при появлении разницы давлений в опыте без введения присадки и с присадкой.

В экспериментальных точках от С1 до С3 происходит увеличение расхода жидкости при сохранении давления с контрольным опытом без присадки, поэтому никаких различий в величине эффекта Томса найденных по двум формулам не наблюдается. Далее в точке С4 расход жидкости в сравнении с предыдущим опытом (С3) уменьшается. Следует заметить, что при уменьшении расхода также произошло снижение перепада давления, что не определилось по формуле (1.2). Точка С4 на кривой 2 оказалась выше, чем на кривой 1. Величина эффекта Томса точки С4 вычислена с учетом перепада давления и в два раза превышает значения при сравнении с формулой (1.2).

Следующая точка С5 имеет обратные значения: при увеличении расхода увеличился перепад давления и опять же формула (1.2) недостаточно иллюстрирует все изменения в системе. Остальные точки С6÷С8 на обоих кривых имеют одинаковый характер лишь с разницей по перепаду давления.

Таким образом, для определения количественной оценки эффекта Томса будем применять формулу (1.2). Использование формулы (1.2) позволило учесть такие параметры как перепад давления, вязкость жидкости, кроме того подсчет параметров не вызывает сложностей, а их использование позволяет достаточно наглядно иллюстрировать влияние определенных факторов на эффект Томса.