DIM YUMAGULOV

Ufa State Aviation Technical University

FUNCTIONAL MOMENTUM STRATEGIES OF PORTFOLIO MANAGEMENT

Stock exchange is one of the most popular and profitable instruments of money investment. Investors very often try to associate their financial state with not one, but several companies and thus they can diversify their security portfolio. This gives an opportunity to investors to reduce the risk from one company regress and to get a complex profit from the set of securities. Moreover, stock exchange gives wide opportunities for investors to apply different strategies for efficient portfolios obtaining.

The new type of strategies for the securities portfolio management has been proposed – functional momentum strategies. Following these strategies, portfolio reforms by the formal rules at regular time intervals. An empirical research of such strategies has been conducted, which demonstrated their high efficiency for an appropriate choice of parameters.

Functional momentum strategies is based on next parameters.

Reformation period T. We adopted T equal to a week, a month, a quarter, a half-year, a year.

Momentum function f(x). Proportion of shares of a particular type is defined in accordance with the value of momentum function of share yield for the previous period. In the course of this research we considered functions f =; f =; f =; f =; f =; f =1.

Number of shares k. In each time interval portfolio consists of k shares, which values of momentum function became the largest for the previous period. Value of k varied from 1 to n – common number of shares being considered.

Costs for portfolio reformation were considered in this research. It is known that it is necessary to pay a part of share for buy-sell operation. This part is equal to r < 1.

The point of proposed functional momentum strategies of portfolio management is as follows. At the reformation moment t an investor has a shares portfolio. The market value of this portfolio at the moment is 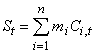, where m_i – number of shares of i-type in the portfolio, C_i,t – share cost at the moment t.

Further, the portfolio will be reformated through the time T by the following algorithm. Let us consider the segment of the market, which consists of the stocks of n issuers. We must calculate the yield through the time T for each type of stocks:

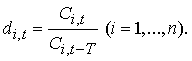
Next, we must calculate value of function for each type of selected stocks:

The part of capital allocated for the purchase of stocks of i-type will be equal

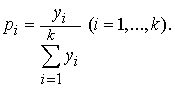
Let A be portfolio value before the reformation. Then, balance equation is:

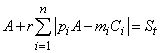
Let p_i equal to 0 for the shares, which will not be included in a new portfolio. Value is equal to the sum for the purchase (sale) of i-type stocks.

The function on the left side, as it is easy to verify, looks piece-wise linear and convex. The equation has the unique solution with respect to A, i.e. the cost of re-formed portfolio and its structure is uniquely determined.

Experimental verification of functional momentum strategies efficiency with the modern computer systems applied let make the next conclusions:

1) Functional momentum strategies are an effective instrument of portfolio management.

1) Investment at term of 5 years most profitable segments of the market are small (2-3 shares) and medium (8-12). And, more often on these segments more effective are the momentum function , small portfolio dimension (3-4 shares) and reformation period of 6 months.

2) In most cases, the next parameters are most profitable: momentum function , portfolio dimension k = 3 and reformation period T = 6 months.

REFERENCES

1. Sergio Ortobelli, Svetlozar Rachev, Isabella Huber, Almira Biglova Optimal Portfolio Selection and Risk Management: A Comparison between the Stable Paretian Approach and the Gaussian One // Handbook of Numerical Methods in Finance, Birkhäuser Boston, 2004, p. 197-252.

2. Jegadeesh, N. and Titman, S., 2001, Profitability of momentum strategies: An evaluation of alternative explanations // Journal of Finance. Vol. 56, pp. 699-720.

3. Chordia, T. and L. Shivakumar, 2002, Momentum, Business Cycles and Time-Varying Expected Returns // Journal of Finance, Vol. 57, pp. 985-1019.

4. Cooper, M. J., Gutierrez, R. C. Jr., and A. Hameed, 2004, Market States and Momentum // Journal of Finance, Vol. 59, 3, pp. 1345-1365.

5. Griffin, J.N, Ji, X. and J.S. Martin., 2003, Momentum investing and business cycle risk: Evidence from pole to pole // Journal of Finance, Vol. 58, pp. 2515-2547.