Экономические науки/8. Математические методы в экономике

К.ф.-м.н. Зинченко А.Б.

Южный федеральный университет. Россия

Техника вывода достаточных условий существования

С-ядра классической кооперативной игры

Интересы участников некоторых экономических ситуаций часто не совпадают, хотя и не являются противоположными. Конфликт заключается в том, что при совместной деятельности (кооперации) каждый старается сократить долю расходов, но увеличить прибыль. Одним из способов "справедливого" распределения общего дохода является использование кооперативной игры , где - множество игроков (агентов), - характеристическая функция, . Значение интерпретируется как доход, который может получить коалиция S независимо от действий остальных агентов. Игра в форме характеристической функции не учитывает многие факторы, свойственные реальным ситуациям (политические или социальные мотивы, личные качества агентов, родственные связи, симпатии и антипатии, возможность влияния на других и т.д.). Их формализация делает модель трудноразрешимой, поэтому кооперативная теория выработала несколько принципов "справедливости", каждый из которых может дать отличный прогноз для одной реальной ситуации и неприемлемые результаты для другой.

Предположим, что игра неотрицательна (, ) и отождествим с функцией . Множество всех неотрицательных игр лиц обозначим через . Для сокращения будем опускать фигурные скобки и запятые при указании коалиций, например, писать вместо , вместо .

Если выгодно объединение всех игроков, то наиболее популярной концепцией решения является -ядро (core) , где - множество эффективных распределений (predimputation set), - множество собственных коалиций. При любом дележе из -ядра суммарный выигрыш каждой коалиции не меньше ее собственной возможности . Игра, имеющая непустое -ядро, называется сбалансированной. Необходимое и достаточное условие сбалансированности игры [1]-[2] имеет вид

, , (1)

где , . Если известны все крайние точки многогранника , то для конкретной функции n условие (1) становится системой числовых неравенств. Общего описания крайних точек пока нет, но вычислено, что: , , , , . Количество неравенств системы (1) резко возрастают при увеличении , поэтому их разбивают на классы эквивалентности , каждый из которых содержит неравенства, отличающиеся перестановкой игроков. Для игры четырех лиц мы имеем 41 неравенство и 9 классов эквивалентности, представители которых приведены во втором столбце таблицы 1.

Таблица 1.

Условие существования -ядра игры четырех лиц

Класс экв-ти	Представитель класса	Мощность класса

Имеются более простые, чем (1), но уже только достаточные условия существования -ядра, наиболее известным из которых является условие выпуклости

, . (2)

Описан метод вывода достаточных условий [3]. В данной заметке предлагается более простой способ, приводятся примеры его реализации.

Рассмотрим систему

,, , (3)

отличающуюся от системы, определяющей -ядро игры тем, что уравнение

(4)

заменено неравенством . Если система (3) неразрешима, то игра не имеет -ядра. Пусть - решение системы (3) . Если удовлетворяет (4), то . В противном случае -ядру принадлежит дележ

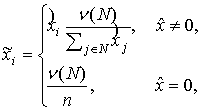(5)

являющийся проекцией на гиперплоскость .

Запишем (3) в виде

, (6)

где , , , для, . Первыми строками матрицы являются характеристические векторы коалиций

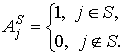(7)

Последняя строка матрицы соответствует максимальной коалиции . Очевидно .

Пусть - базис матрицы (невырожденная квадратная подматрица порядка ), тогда перестановкой строк систему (6) можно привести к виду , , где - подматрица матрицы , состоящая из строк, не вошедших в базис. Уравнения определяют базисное решение системы (5). При выполнении условия

. (8)

будет допустимым решением. Если удовлетворяет (8) и базис содержит строку , то для выполняется (4), следовательно, . В противном случае, соответствующий элемент -ядра можно вычислить, используя формулу (5). Таким образом, условие (8) выделяет подмножество (многогранный конус) сбалансированных игр , соответствующий базису .

В примерах 1 и 2 (ниже) получен явный вид условия (8) для игры лиц и двух базисов, один из которых не содержит строку , а другой – содержит.

Пример 1. Рассмотрим в начале самый простой базис , состоящий из характеристических векторов всех одноэлементных коалиций. Из (7) следует, что и - единичные матрицы порядка , . Условие (8) принимает вид

,, ,

и определяет множество сбалансированных игр, содержащее аддитивные игры.

Пример 2. Возьмем базис , полученный из базиса примера 1 заменой строки на . Тогда

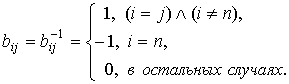
Вектор , где

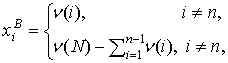
принадлежит -ядру и совпадает с одной из крайних точек множества дележей (imputation set) игры . При дележе выигрыш каждого агента минимален (он получает то, что может иметь без кооперации с остальными игроками). Выигрыш -го агента равен остатку кооперативной прибыли (surplus). Если является игрой большого босса (big boss game) [4] с игроком в качестве босса, то определенный (9) дележ является "точкой босса". Условие (8) принимает вид

, , .

и выделяет подмножество сбалансированных игр, -ядро которых содержит крайнюю точку симплекса . Аналогично определяется подмножество игр, содержащих любой другой элемент из .

В следующем примере рассматриваются игры с фиксированным количеством участников . Описан класс игр, -ядро которых содержит одну из крайних точек , ,

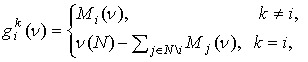(9)

множества двойственных дележей (dual imputation set) , где - вклад игрока в максимальную коалицию. Дана содержательная интерпретация неравенств системы (8).

Пример 3. Пусть . Возьмем базис , содержащий кроме характеристические векторы -элементных коалиций. Используя (7), получаем

, ,

.

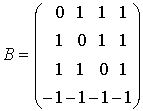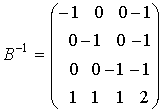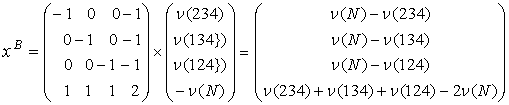Видно, что совпадает с крайней точкой (см. формулу (9)) множества . Подставив , и в (8), имеем

.

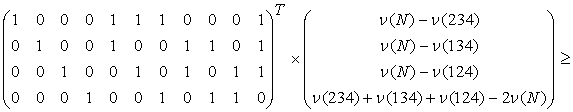
Условие (8), соответствующее выбранному базису, состоит из 11 (вместо 41, составляющих систему (1)) неравенств, приведенных во втором столбце таблицы 2.

Таблица 2.

Достаточное условие существования -ядра игры четырех лиц

№	Неравенство	Преобразованное неравенство
1
2
3
4
5
6
7
8
9
10
11

Первые 7 неравенств содержатся в системе (1). Они принадлежат классам , , (см. таблицу 1). Остальные 4 неравенства известны как "условие союза" и используются при определении игр большого босса. Преобразованные неравенства (третий столбец таблицы 2) допускают следующую интерпретацию. Значение каждой коалиции , не содержащей четвертого игрока, должно быть не больше суммы вкладов ее участников в максимальную коалицию. Неравенства 8-11 означают, что вклад каждой такой коалиции () в , наоборот, должен быть не меньше суммы вкладов , . Умноженные на (-1) неравенства 9-11 содержатся в (2). Следовательно, для выбранного базиса, система (8) содержит часть неравенств из условия вогнутости игры. Неравенства 1-3 являются частью условия супераддитивности

+£, , .

которое означает, что две непересекающиеся коалиции после объединения могут обеспечить себе не меньший доход, чем, действуя самостоятельно.

Литература:

1. Shapley L. S. On balanced sets and cores // Naval Research Logistics Quarterly. 1967. V. 14. P. 453-460.

2. Бондарева О.Н. Некоторые применения методов линейного программирования к теории кооперативных игр // Проблемы кибернетики. 1963. Вып. 10. М.: Физматгиз. С. 119-140.

3. Зинченко А.Б., Головань С.В. Достаточное условие существования с-ядра кооперативной игры // Известия высших учебных заведений. Северо-Кавказский регион. Естественные науки. 2001. №1. С. 8-11.

4. Muto S., Nakayama M., Potters J., Tijs S. On big boss games // The Economic Studies Quarterly. 1988. № 39. P. 303-321.