Современные информационные технологии. 1. Компьютерная инженерия

К.х.н. Туманов В.Е.

Институт проблем химической физики РАН, Россия

НЕЧЕТКАЯ БАЗА ЗНАНИЙ ДЛЯ ПРЕДСКАЗАНИЯ РЕАКЦИОННОЙ СПОСОБНОСТИ РЕАКЦИЙ ФЕНИЛ РАДИКАЛОВ С УГЛЕВОДОРОДАМИ

В результате научных исследований накоплены огромные массивы научных данных о характеристиках химических реакциях (константах скорости, энергиях активации, энтальпиях реакции), которые аккумулируются в электронных ресурсах. Экспериментальное определение констант скорости и энергий активации радикальных реакций является сложной экспериментальной задачей, и во многих практических случаях ее теоретическая оценка является актуальной задачей.

Начало исследований по предсказании энергии активации радикальных реакций по эмпирическим данным было положено известным линейным соотношением Поляни-Семенова [1], и дальнейшем получило свое развитие в работах [2,3]: корреляционные уравнения в рамках модели пересекающихся парабол и пересекающих термов Морзе. Методикам идентификации нелинейных, в том числе и эмпирических зависимостей нечеткими базами знаний посвящено достаточно много работ, обстоятельный обзор которых можно найти в монографии [4].

Целью настоящей работы является разработка нечеткой базы знаний для идентификации эмпирической зависимости энергии активации реакций фенил радикалов (C₆H^º₅, 4-CH₃- C₆H^º₅, 4-Br-C₆H^º₅, 4-Cl-C₆H^º₅ и т. д.) с углеводородами в жидкой фазе для предсказания последней.

Для определения пространства параметров идентификации (входных данных) энергии активации радикальной реакции E_экс в настоящей работе используется модель пересекающихся термов Морзе, которая определяется корреляционным соотношением [3]:

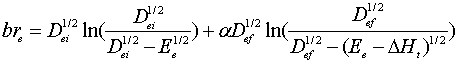(1)

Параметры, входящие в формулу (1) имеют следующий смысл:

1) DH_e = D_i - D_f + 0,5 (hLn_i - hLn_f) – энтальпия реакции включающая разницу энергий нулевых колебаний рвущейся и образующейся связей. Здесь h – постоянная Планка, L – число Авогадро, n_i – частота колебания молекулы вдоль разрываемой связи, n_f – частота колебания молекулы вдоль образующейся связи, D_i – энергия диссоциации разрываемой связи, D_ei = D_i + 0,5hLn_i, D_f – энергия диссоциации образующейся связи, D_ef = D_f + 0,5hLn_f. 2) E_e = E_экс – 0.5(hLυ_i – RT) -классический потенциальный барьер активации, который включает в себя энергию нулевого колебания рвущейся связи, R – газовая постоянная, T – температура в К. 3) Параметры b = p(2m_i)^1/2n_i и b_f = p(2m_f)^1/2n_f описывают зависимость потенциальной энергии от амплитуды колебаний атомов вдоль рвущейся (i) и образующейся (f) валентной связи. 2b² – силовая постоянная связи, m_i – приведенная масса атомов для разрываемой связи, m_f – приведенная масса атомов для образующейся связи. 4) Параметр r_e равен суммарному растяжению рвущейся и образующейся связей в переходном состоянии. 5) Параметр a² - равен отношению силовых постоянных рвущейся и образующейся связей.

Предполагается, что классический потенциальный барьер активации задается нелинейным объектом (параметр a остается постоянным для всей выборки):

(2)

Для моделирование зависимости используются два качественных параметра S₁ – характеристика реакционного центра углеводорода (определяемая классом соединения, рассматривается 40 классов) и S₂ – характеристика растворителя (неполярный, полярный, комплексообразующий полярный, комплексообразующий неполярный) [5]. Выборка (647 реакций) получена из базы данных по константам скорости радикальных жидкофазных реакций предметно-ориентированной системы научной осведомленности по физической химии радикальных реакций [6]. Особенностью выборки является сочетание количественных и качественных параметров в одной модели идентификации.

При построении нечеткой базы данных входные и выходная переменные в зависимости (2) рассматриваются как лингвистические переменные, заданные на соответствующих универсальных множествах. В качестве функции принадлежности элемента к нечеткому терму G выбрана:

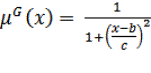(3)

где начальные значения параметров b и с были выбраны экспертным образом. Нечеткая база знаний задается системой логических высказываний в виде:

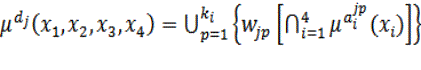(4)

Где x₁÷x₄ – лингвистические оценки входных переменных D_ei, D_ef, S₁, S₂; d_j – лингвистическая оценка выходной переменной E_e, w_jp – весовая матрица правил.

Для экспериментальной выборки для реакций фенил радикалов с углеводородами нечеткая база знаний была настроена с помощью генетического алгоритма [4]. В настоящий момент она включает 634 нечетких правила.

В Табл. 1 приведено сравнение значений классического потенциального барьера активации реакции фенил радикалов с углеводородами E_e, полученных с помощью нечеткой базы знаний, с вычисленными по экспериментальным значениям энергии активации E_{кл_экс} соответствующих реакций.

Таблица 1. Сравнение значений классического потенциального барьера активации реакции фенил радикалов с углеводородами.

Радикал	Углеводород	Растворитель	Ee, кДж/моль	Eкл_экс, кДж/моль
C6H5º	цикло-[CH=CHCH=CH(CH2)2]	Неполярный с комплексом	12,01	11,96
C6H5º	C6H5CH(CH3)2	Полярный с комплексом	21,10	21,06
C6H5º	(CH3)2CHOH	Полярный	21,40	21,37
C6H5º	(CH3)2CHOH	Полярный	21,46	21,44
C6H5º	cyclo-[CH=CH(CH2)4]	Полярный	21,78	21,81
C6H5º	C6H5CH2OH	Полярный с комплексом	21,90	21,86
4-NO2-C6H5º	C6H5CH(CH3)2	Неполярный с комплексом	24,0	23,98
C6H5º	C6H5CH(CH3)2	Неполярный с комплексом	24,0	23,98
4-Br-C6H5º	C6H5CH(CH3)2	Неполярный с комплексом	24,41	24,38
C6H5º	C6H5CH2CH3	Полярный	24,43	24,42
C6H5º	CH3CH2OH	Полярный с комплексом	24,50	25,51
C6H5º	C6H5C(CH3)2CH(O)	Неполярный с комплексом	25,58	25,55

Как видно из Табл. 1, наблюдается хорошее согласие между экспериментальными и полученными путем нечеткого логического вывода значениями классического потенциального барьера активации.

Таким образом, впервые на примере реакций фенил радикалов с углеводородами была выполнена попытка идентифицировать зависимость классического потенциального барьера активации радикальной реакции нечеткой базой знаний, построенной на основе количественных и качественных параметров.

Литература:

1. Семенов Н. Н. О некоторых проблемах химической кинетики и реакционной способности. Изд-во АН СССР. Москва. 1958. 686 с.

2. Денисов Е.Т. Нелинейные корреляции в кинетике радикальных реакций. Препринт ОИХФ АН СССР. Черноголовка. 1990. 18 с.

3. Денисов Е.Т., Туманов В.Е. Модель переходного состояния как результат пересечения двух термов Морзе в приложении к реакциям атомарного водорода // Журнал физической химии. 1994. Т. 68. № 4. С. 719-725.

4. Митюшкин Ю.М., Мокин Б.И., Ротштейн А.П. Soft Computing: идентификация закономерностей нечеткими базами знаний. Вiнниця. УНIВЕРСУМ- Вiнниця. 2002. 145 с.

5. Денисов Е.Т., Туманов В.Е., Денисова Т.Г., Дроздова Т.И., Покидова Т.С. Реализация Банка кинетических констант радикальных жидкофазных реакций на IBM PC/AT. Черноголовка. ИХФЧ РАН. Препринт. 1992. 58 с.

6. Туманов В.Е., Прохоров А.И., Лазарев Д.Ю., Соловьева М.Е. Система научной осведомленности по физической химии радикальных реакций. // Информационные ресурсы России. 2010. № 5. С. 16-21.