СОВРЕМЕННЫЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ / 2. Вычислительная техника и программирование

д.т.н. Дулесов А. С., Гаврилова Т. В., Хрусталев В. И., Хрусталев Р. И.

Хакасский государственный университет им. Н.Ф. Катанова

Выбор структуры системы управления на основе меры неопределенности информации

Повышение эффективности производства связано с необходимостью создания современной системы управления, обеспечивающей слаженность функционирования структурных подразделений. Однако любая система несет на себе печать неопределенности информации в процессе управления, которую желательно снять или уменьшить. Одним из путей решения такого рода задачи можно считать выбор эффективной структуры управления через меру неопределенности информации (энтропию). Практически любая система управления имеет структуру или может быть представлена в виде графа, на основе которого вычисляется энтропия. Анализируя факторы воздействия на систему, можно на основе значений энтропии видеть, например, степень согласованности или несогласованности между собой управленческих действий, выбирать из различных вариантов структур (схем) управления наиболее приемлемую с точки зрения наличия неопределенности.

Опираясь на предложенный в [1] метод определения энтропийной меры структурной сложности (или простоты) систем управления, предложим далее его практическую реализацию.

Процесс вычисления энтропии заключается в нижеследующем:

1. Имеющаяся структура системы управления, состоящая из подразделений (или элементов) отображается в виде графа: вершина отражает наличие в системе подразделения; ребро – связь между двумя подразделениями. Связь отражает наличие отношения между подразделениями: непосредственное управление; непосредственное подчинение; косвенное управление; косвенное подчинение и др.

2. Составляется список отношений r₁, ..., r_k, …, r_K из K наименований. Единичное отношение r_k(l_ij), имеющее экстенсиональную длину l_ij = 1, приписывается каждой дуге i-j графа, связывающей между собой два элемента i и j.

3. Выполняется распределение l_ij по всем имеющимся отношениям r_k→[Ώ_k], где Ώ_k – множество пар номеров элементов (вершин графа), связанных данным отношением. Единичные отношения определяют экстенсиональную длину по выражению: 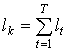, где t – порядковый номер пары из множества Ώ_k, T – общее количество пар множества Ώ_k, l_t – единичная экстенсиональная длина дуги (пары).

4. Имея все многообразие отношений (списков) r₁ → [Ώ₁], r₂ → [Ώ₂],…, r_k → [Ώ_k],…, r_K → [Ώ_K] для каждой вершины графа формируется массив отношений: m_i → [Θ_│i→k], в котором Θ_│i→k – пара с номером i-j с приписанным r_k-м отношением. Количество массивов m_i должно быть равно M, то есть числу вершин графа.

5. На основе всех одномерных массивов m_i создается двумерный массив, вида: l_ik , (i=1, 2,…, М), (k=1, 2,…, K), где l_ik – экстенсиональная длина элемента i в k-м отношении, M – количество вершин графа, K – количество отношений в графе.

6. На основе двумерного массива экстенсиональных длин определяется величина вероятности пребывания элемента i в k-м отношении по выражению: p_ik = l_ik/l_i при условии, что сумма всех полученных p_ik по строкам массива l_ik должна быть равна 1.

7. Через вероятности p_ik по формуле Шеннона определяется энтропия, приходящаяся на одно отношение r_k и один элемент m_i:

.

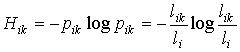8. Общая энтропия системы управления, имеющая отношение к структуре вычисляется по формуле:

.

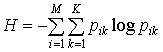Величину H можно рассматривать как меру сложности структуры. Обратное значение этой величины будет мерой структурной простоты.

Рассматривая несколько вариантов систем управления одной структуры, определив величины H для каждого варианта, можно судить о его сложности. Вариант системы, у которого мера максимальна, является максимально сложным.

Представленный метод реализован на примере двух вариантов структур системы управления производственным процессом (рис. 1 и рис. 2). Список отношений, связывающих элементы структуры, и их условные обозначения приведены в таблице 1.

Табл. 1 Список отношений в системе управления

№	Отношение	Условное обозначение
1	Непосредственное управление (подчинение) (r1)
2	Косвенное управление (подчинение) (r2)
3	Функциональные связи между элементами (отчеты, приказы, распоряжения и т.п.) (r3)
4	Информационные потоки между элементами структуры (r4)

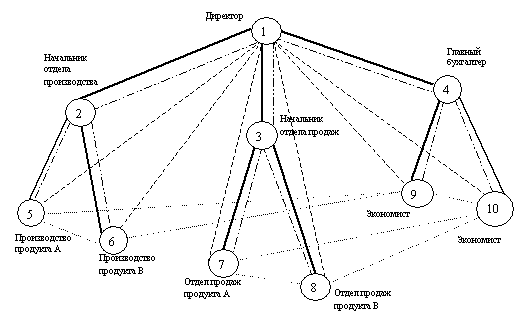
Рис. 1 – Вариант линейной структуры управления

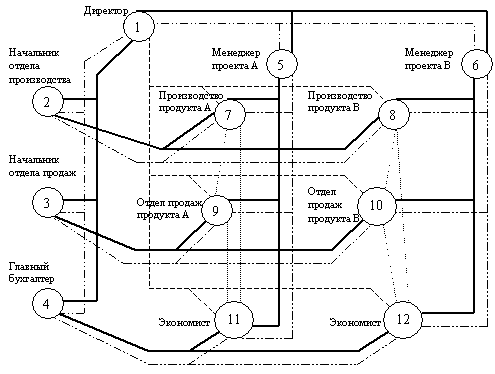
Рис. 2 – Вариант матричной структуры управления

Между вариантами управления имеется разница как в количестве структурных единиц управления, так и числе намеченных связей между ними.

Согласно предложенному алгоритму, используя MSExcel, вычислены общие энтропии систем управления:

- для первого варианта H₁ = 4.75;

- для второго варианта H₂ = 5.50.

Таким образом, при прочих равных условиях, первый вариант структурной сложности управления предприятием является предпочтительнее.

В матричной структуре управления энтропия возрастает из-за системы двойного подчинения исполнителей, то есть сотрудники производственного и экономического отдела, отвечающие за производство одного вида продукции, одновременно подчиняются двум руководителям – начальникам отделов и менеджеру, курирующему данный проект. Поэтому каждому из начальников направляются различного вида отчеты и от каждого из них получают различные распоряжения. Неопределенность возникает из-за перегрузки и сбоев производственного звена. Такие недостатки присущи практически любым матричным структурам и их применение возможно не для всей компании в целом, а лишь для отдельных её частей. Линейная система управления обладает меньшей сложностью, поскольку над каждым отделом закреплен только один непосредственный начальник.

Данный метод ориентирован на выбор эффективного варианта из многообразия вариантов и, следовательно, позволяет понизить риск принятия руководителем правильного решения при построении организационной структуры.

Литература

1. Дулесова Н. В., Хрусталев В. И. Совершенствование системы управления производством: определение энтропийной меры ее субстрактно-структурной сложности // Перспективы науки. – 2010. – № 8(10). – C. 33–37.