Современные информационные технологии
Вычислительная техника и программирование
к.т.н. Буянкин В.М.,
Московский государственный технический
университет им. Н.Э.Баумана,
к.
физ-мат. н. Ковалева С.К.
РНЦ ” Курчатовский институт”
Нечеткие технологии синтеза
для нейроуправления сложными нелинейными технологическими устройствами с
неопределенными характеристиками
Метод решения проблемы
Разработаем нечеткую модель
гибридной нейронной сети для скоростного контура станочного электропривода [3].
В качестве исходных данных воспользуемся информацией диаграммы устойчивости
рис. 1 скоростного контура от значения таких входных переменных, как
коэффициент жесткости L1.2п,
коэффициент демпфирования H1.2п,
момент инерции механической передачи J2п и
выходная переменная интегрального коэффициента регулятора Kiск.
Нечеткая модель гибридной сети будет содержать 3 входные переменные и
одну выходную переменную. Данную информацию для удобства представим в табличной
форме (табл.1).
Таблица 1.
Три входных параметра и один выходной параметр механической части
электропривода
|
Первая входная переменная коэффициент жесткости L1.2п |
Вторая входная переменная коэффициент демпфирования H1.2п |
Третья входная переменная момент инерции J2п |
Выхо дная переменная интегральный коэффициент Ki ск |
|
1 |
1 |
1 |
0.5 |
|
2 |
2 |
2 |
1 |
|
3 |
3 |
3 |
1.5 |
|
4 |
4 |
4 |
2 |
|
5 |
5 |
5 |
2.5 |
|
6 |
6 |
6 |
3 |
|
7 |
7 |
7 |
3.5 |
|
8 |
8 |
8 |
4 |
|
9 |
9 |
9 |
4.5 |
|
10 |
10 |
10 |
5 |
Сохраним обучающую выборку в рабочей области МАТЛАБ переменной р2
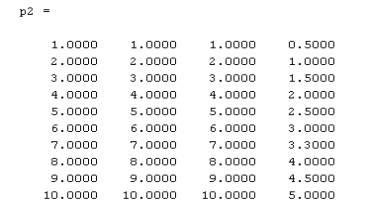
Заходим в редактор
нечеткого вывода FIS с помощью функции fuzzy
рис. 2.
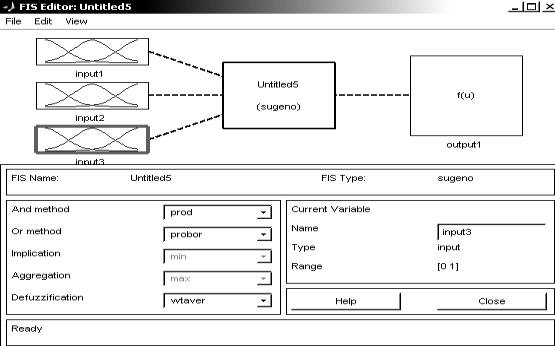
Рис. 2. Редактор нечеткого вывода FIS
Введем обучающую
выборку р1 в редактор FNIS
рис. 3. Перед генерацией
структуры Сугено после вызова диалогового окна свойств зададим для каждой из
входных переменных по 3 лингвистических терма, а в качестве типа их функций
принадлежности выберем треугольные функции. В качестве функции принадлежности
зададим линейную функцию рис. 4.
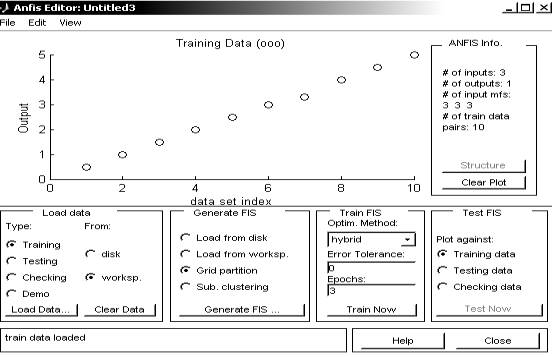
Рис. 3. Обучающая выборка р2
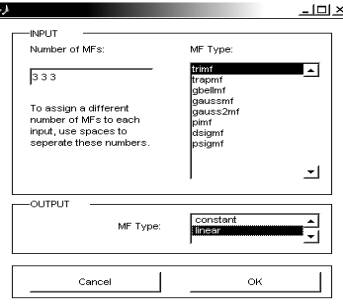
Рис. 4. Функции принадлежности
Для обучения гибридной
сети воспользуемся гибридным методом
обучения с уровнем ошибки 0, а количество циклов обучения зададим равным 20
рис. 5.
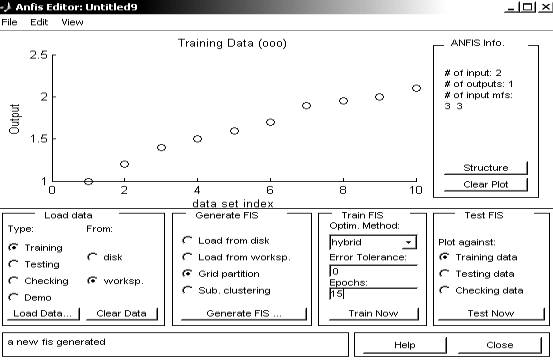
Рис. 5.
Задание ошибки 0, количество
циклов обучения 20
На рис. 6 представлена ошибка обучения
гибридной сети
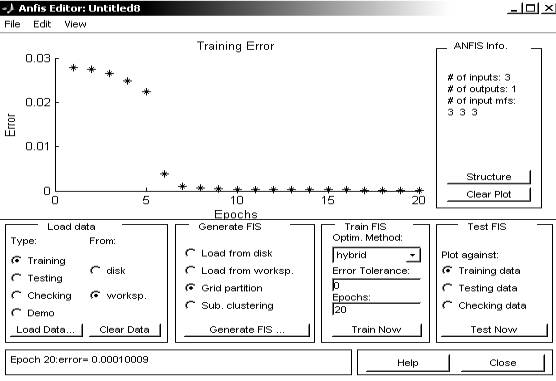
Рис. 6. Ошибка обучения гибридной сети.
После окончания обучения данной гибридной сети выполним анализ графика
ошибки обучения, который показывает, что обучение практически закончилось после
7 цикла. После обучения можно
визуально оценить структуру построенной нечеткой гибридной сети рис. 7.
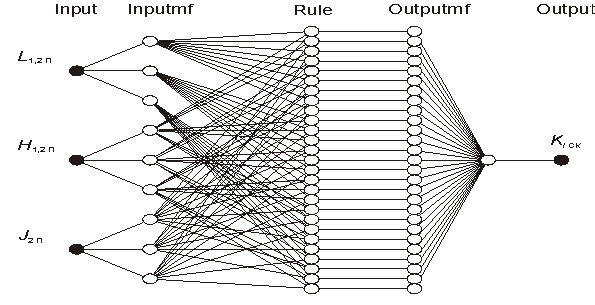
Рис. 7. Структура построенной нечеткой гибридной сети.
Слой 1 Input входной
слой гибридной нейронной сети для фазификации.
Слой 2 Inputmf выходы
нейронов этого слоя представляют собой значения функций принадлежности при
конкретных значениях входов.
Слой 3 Rule выходами
нейронов этого слоя являются степени истинности предпосылок каждого правила
базы значений системы. Все нейроны этого слоя могут реализовывать
произвольную L- норму для моделирования операции «И».
Слой 4 Outputmf нейроны этого слоя вычисляют формируют
значения выходов переменных.
Слой 5 Output нейроны
данного слоя выполняют
операцию дефазификации
Выполним проверку адекватности построенной нечеткой модели гибридной
сети. Введем на вход нечеткой гибридной
сети L1.2п= 5, H1.2п=5, J2п=5;
на выходе получим Kiск=2,5.
Сравнивая полученный выход
нечеткой гибридной сети с табл. 3.4
можно констатировать абсолютное совпадение этих значений.
На рис. 8 представлен переходной
процесс в скоростном контуре с рассчитанными параметрами.
На рис. 9 представлена система управления скоростным и токовым контурами
электропривода с нечеткими гибридными сетями.
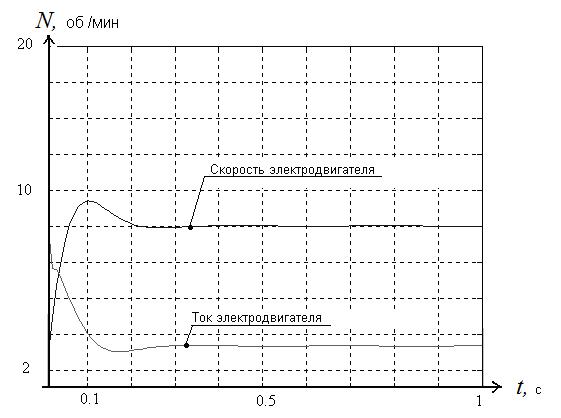
Рис. 8.
Переходной процесс в скоростном контуре с рассчитанными
параметрами.
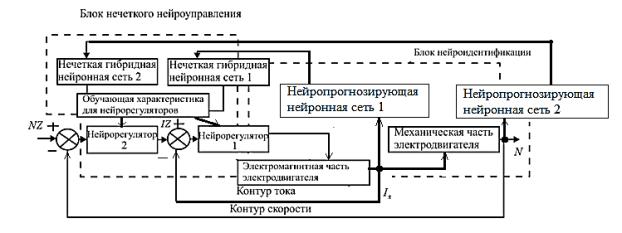
Рис. 9. Система управления токовым и скоростным
контурами электропривода с нечеткими гибридными сетями
Выводы
В заключение можно сделать
выводы, что нейропрогнорзирующий метод нейроуправления нелинейными технологическими
устройствами с нечеткой логикой на базе нейрорегуляторов, эффективность которого была
проверена на одноконтурной,
двухконтурной и трехконтурной системах нейроуправления, работающего по принципам нейроподчиненного регулирования
электроприводом показал, что точность работы за счет этой системы нейроуправления увеличилась на 12% по сравнению с
традиционными и классическими системами управления.
Литература:
1. Буянкин В.М. Применение нейронных
сетей для управления” Нейросетевые методы повышения эффективности систем
управления сложными элементами электротехнических установок” Издание LAMBERN Academic Publishing
Germany, 2011г 265с.
2. Буянкин В.М. Нейроуправление
роботами с параллельной кинематикой “ Применение нейронных сетей для управления
роботами” Издание LAMBERN Academic Publishing
Germany, 2011г 167 с.
3. Буянкин В.М. Цифровое управление электродвигателями.
“Микропроцессорный следящий электропривод.” Издание LAMBERN Academic Publishing
Germany, 2012г.
180 с.