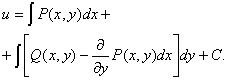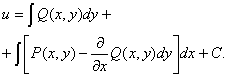Шацкая Л.С.

Актюбинский политехнический колледж, преподаватель, Казахстан

Организация коллективной познавательной деятельности учащихся при изучении темы: «Решение уравнений в полных дифференциалах»

Организация коллективной познавательной деятельности предусматривает такие методы и приемы осуществления учебно –познавательного процесса, при которых между учащимися возникают отношения взаимозависимости и взаимоответственности, характеризующиеся интенсивным сотрудничеством.

Коллективная познавательная деятельность может осуществляться при групповой форме обучения. Самым простым видом групповой формы является парная работа учащихся.

Рассмотрим пример организации парной работы при изучении темы «Решение уравнений в полных дифференциалах» так называемым «зеркальным способом».

Напомним кратко основные положения теории.

Определение. Дифференциальное уравнение первого порядка вида:

называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции

Интегрирование такого уравнения сводится к нахождению функции u, после чего решение легко находится в виде:

Таким образом, для решения надо определить:

1) в каком случае левая часть уравнения представляет собой полный дифференциал функции u; 2) как найти эту функцию.

Если дифференциальная форма является полным дифференциалом некоторой функции u, то можно записать:

т.е. .

Необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом, называется условием тотальности.

Теперь рассмотрим вопрос о нахождении собственно функции u. Рассмотрим алгоритм решения уравнений в полных дифференциалах «зеркальным способом».

Проинтегрируем: равенство по переменной х,	Проинтегрируем: равенство по переменной у
Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию f(у), т.к. при интегрировании переменная у полагается постоянным параметром.	Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию f(х), т.к. при интегрировании переменная х полагается постоянным параметром.
Определим функцию f(у).	Определим функцию f(х).
Продифференцируем полученное равенство по у.	Продифференцируем полученное равенство по х.
Откуда получаем:	Откуда получаем:
Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство.	Для нахождения функции С(х) необходимо проинтегрировать приведенное выше равенство.
Подставляя этот результат в выражение для функции u, получаем:	Подставляя этот результат в выражение для функции u, получаем:

Следует отметить, что при решении уравнений в полных дифференциалах не обязательно использовать полученную формулу. Решение может получиться более компактным, если просто следовать методу.

Так, при закреплении изученного материала, можно организовать решение уравнения с использование двухсторонней парной работы, при которой двое учащихся решают параллельно одно уравнение. Но отличие состоит в том, что в первом случае решение начинается с верхней производной , а во втором - с нижней производной . В процессе решения учащиеся контролируют друг друга и оказывают взаимопомощь.

Пример. Решить уравнение

Проверим условие тотальности:

Условие тотальности выполняется, следовательно, исходное дифференциальное уравнение является уравнением в полных дифференциалах. Определим функцию u.

Проинтегрируем: равенство по переменной х,	Проинтегрируем: равенство по переменной у
Продифференцируем полученное равенство по у.	Продифференцируем полученное равенство по х.
Находим общий интеграл исходного дифференциального уравнения:	Находим общий интеграл исходного дифференциального уравнения:

Эффективность «зеркального способа» заключается в том, что нет необходимости выполнять отдельно проверку. Если в последнем действии алгоритма получаются одинаковые функции u, то уравнение решено верно.

Литература:

1. В.П.Минорский «Сборник задач по высшей математике»
2. Сайт Informpro.ru
3. Сайт КВМ Ларин