Математика /1. Дифференциальные и интегральные уравнения

проф. В.В. Городецький, к.ф.м.н. Р.С. Колісник, к.ф.м.н. Н.М. Шевчук

Чернівецький національний університет імені Юрія Федьковича, Україна

- точкова за часом задача для одного класу еволюційних рівнянь

У праці [1] введені простори типу , зокрема, простори , які будуються за допомогою функцій та , заданих на . Так, за означенням,

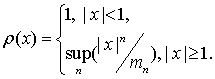
Тут - монотонно зростаюча послідовність додатних чисел, яка володіє властивостями:

1)

2)

3)

- неперервна, парна на функція, яка монотонно зростає на і задовольняє умову .

Наприклад, якщо то .

Функція визначається формулами:

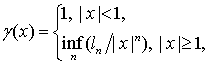
де монотонно зростаюча послідовність додатних чисел володіє властивостями 1)-3). Оскільки , де

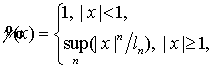
а властивості функцій типу відзначені вже вище, то звідси дістаємо, що - невід’ємна, парна на функція, яка монотонно спадає на проміжку і задовольняє умову

.

Наприклад, якщо , то задовольняє нерівності

За означенням [1], елементами простору є цілі функції , які задовольняють умову: .

є лінійним простором зі звичайними операціями додавання функцій та множення їх на число. В вводиться топологія індуктивної границі зліченно-нормованих просторів , де складається з тих функцій , для яких справджуються нерівності

, де при цьому

.

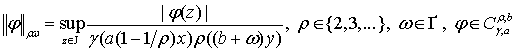У просторі визначені і є неперервними операції множення на , зсуву аргументу та диференціювання. За певних умов на цілу функцію 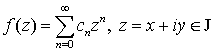, у просторі визначений і є неперервним оператор 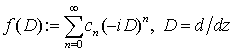, який надалі називатимемо оператором диференціювання нескінченного порядку.

Символом позначимо сукупність нескінченно диференційовних функцій, заданих на , які допускають аналітичне продовження у всю комплексну площину і як функції комплексної змінної є елементами простору .

Якщо - звуження оператора на , то для довільної функції правильною є рівність [1]

(тут - пряме та обернене перетворення Фур’є).

Символом позначимо клас цілих однозначних функцій , які є мультиплікаторами у просторі і такими, що .

Розглянемо еволюційне рівняння

, (1)

де оператор диференціювання нескінченного порядку побудований за функцією . Для (1) задамо граничну умову

, (2)

де - фіксовані числа, причому ( - простір, топологічно спряжений до простору зі слабкою збіжністю; елементи з простору називаються узагальненими функціями).

Тут

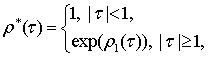
- функція, двоїста за Юнгом [2] до функції -

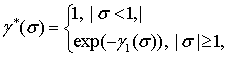
- функція, двоїста за Юнгом до функції .

Під розв’язком нелокальної -точкової за часом задачі (1), (2) розумітимемо функцію яка є розв’язком рівняння (1) і задовольняє умову (2) в тому сенсі, що

,

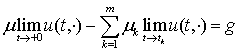де границі розглядаються в просторі .

Правильним є наступне основне твердження.

Теорема. Задача (1), (2) коректно розв’язна. Розв’язок зображається формулою

де

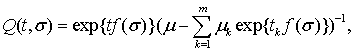
при кожному .

Література

1. Городецький В.В. Задача Коші для еволюційних рівнянь нескінченного порядку. – Чернівці: Рута, 2005.-291с.

2. Гельфанд И.М., Шилов Г.Е. Некоторые вопросы теории дифференциальных уравнений. – М.:Физматгиз, 1958. - 275c.