к.ф.-м.н., доцент Водахова В.А.
Кабардино-Балкарский государственный
университет им. Х.Ю. Бербекова, Россия
Нелокальная задача
для нагруженного гиперболо – параболического уравнения третьего порядка.
Рассматривается уравнение
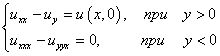 (1)
(1)
в
конечной области ![]() , ограниченной отрезками
, ограниченной отрезками ![]() и
и ![]() прямых
прямых ![]() соответственно, и
характеристиками
соответственно, и
характеристиками ![]() уравнения (1) при
уравнения (1) при ![]() .
.
Пусть ![]() . Под регулярным решением уравнения (1) понимается функция
. Под регулярным решением уравнения (1) понимается функция ![]() , обладающая непрерывными частными производными до порядка,
входящего в уравнение (1) и обращающее его в тождество.
, обладающая непрерывными частными производными до порядка,
входящего в уравнение (1) и обращающее его в тождество.
Задача
1. Найти регулярное в области ![]() решение уравнения
(1), непрерывное в
решение уравнения
(1), непрерывное в ![]() , удовлетворяющее следующим условиям
, удовлетворяющее следующим условиям
![]() (2)
(2)
![]() (3)
(3)
где ![]() внутренняя нормаль,
внутренняя нормаль, ![]() заданные функции, причем
заданные функции, причем
![]() ;
;
![]() и условиям
склеивания
и условиям
склеивания
![]() .
.
Выписывая решение уравнения (1) в области ![]() и, удовлетворяя
краевым условиям (3), получим функциональное соотношение между
и, удовлетворяя
краевым условиям (3), получим функциональное соотношение между ![]() и
и ![]() , принесенное на
, принесенное на ![]() из гиперболической
части области
из гиперболической
части области ![]()
![]() , (4)
, (4)
где
![]()
Функциональная
связь между ![]() и
и ![]() , принесенная из параболической части
, принесенная из параболической части ![]() области
области ![]() получается из
уравнения (1) при
получается из
уравнения (1) при ![]()
![]() . (5)
. (5)
Исключая
из (4) и (5) ![]() , получаем обыкновенное дифференциальное уравнение второго
порядка
, получаем обыкновенное дифференциальное уравнение второго
порядка
![]() . (6)
. (6)
С
учетом краевых условий (2) получаем двухточечную краевую задачу для
обыкновенного дифференциального уравнения
![]() ,
,
![]()
решение
которой имеет вид
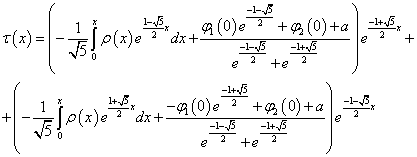
Тогда
задача 1 сводится к следующим двум задачам:
Задача А:
![]()
![]()
![]() .
.
Задача В.
![]()
![]() ,
,
![]() .
.
Решение
задачи А представлено в виде
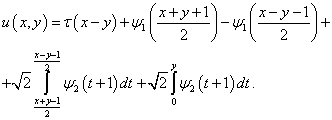
Решение
задачи В имеет вид
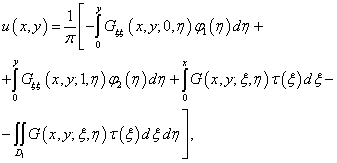
где
![]() функция Грина первой краевой задачи для уравнения
теплопроводности.
функция Грина первой краевой задачи для уравнения
теплопроводности.
Аналогично исследован вопрос
однозначной разрешимости краевой задачи.
Задача
2. Найти функцию ![]() , которая удовлетворяет условиям:
, которая удовлетворяет условиям:
1)
![]()
2)
![]() является регулярным
решением уравнения (1) в
является регулярным
решением уравнения (1) в ![]() ,
, ![]() ;
;
3)
![]() удовлетворяет
условиям
удовлетворяет
условиям
![]()
![]() ,
,
![]()
где
![]() точка пересечения
характеристик уравнения
точка пересечения
характеристик уравнения ![]() выходящих из точки
выходящих из точки ![]() с характеристикой
с характеристикой ![]() .
.
Литература
1. Джураев Т.Д. Краевые задачи для уравнений смешанного и
смешанно-составного типов, изд. «ФАН», Ташкент, 1979 г.
2. Нахушев А.М. Краевые задачи для нагруженных
интегро-дифференциальных уравнений гиперболического типа и некоторые их
приложения к прогнозу почвенной влаги. Дифференц. уравнения, т.15, №12, 1979 г.
3. Елеев В.А., Макоева М.Х. О некоторых краевых задачах
для смешанных уравнений гиперболо - параболического типа второго и третьего
порядка. Нальчик, Известия КБНЦ РАН, №1(8), 2002 г.