Аубакирова З.Ж., Акишев Г.

Карагандинский государственный университет

имени Е.А.Букетова, Казахстан

Абсолютная сходимость лакунарных рядов Фурье

Пусть . Через обозначается совокупность всех измеримых по Лебегу, - периодических функций, для которых ([1])

(1)

- коэффициент Фурье функции по системе .

Рассматривается лакунарный ряд

где -строго возрастающая последовательность натуральных чисел ([1]).

Пусть - класс функций, определенных и непрерывных на c нормой .

- обозначим наилучшее приближение функции тригонометрическими полиномами порядка не выше .

Определение ([2]). Строго возрастающая последовательность натуральных чисел, удовлетворяет условию : если конечен, где обозначает число различных представлений целого числа в виде .

Рассматривается следующий вопрос: при каких условиях, наложенных на функцию , определенную на и числовую последовательность можно утверждать, что для функции ряд

?

Эту задачу ранее исследовали С.Б.Стечкин [3] для , Чан Минь [4] для , , Ж.Р. Патадиа и В.М. Шах [5] для , а для возрастающей и вогнутой функции и исследовал Н. Огата [2], при Л. Лейндлер [6].

В предлагаемом докладе рассмотрены обобщения их результатов.

Лемма 1. Пусть функция определена для , возрастающая и вогнутая, такая, что , а - монотонно не возрастающая функция. Тогда для любой положительной неубывающей последовательности следующие два условия

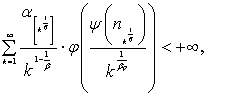(2)

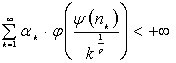(3)

эквивалентны, где , Доказывается как лемма 2 в [2].

Теорема 1. Пусть , ~

и функция определена для , возрастающая, вогнутая и возрастающая последовательность, для любого удовлетворяет условию

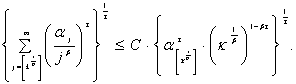(4)

Если

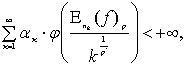
то

.

Доказательство. Пусть Воспользуемся неравенством Иенсена ([1. С.899]). Тогда

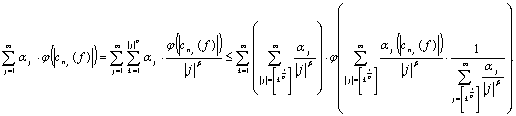(5)

Применяя неравенство Гёльдера получим

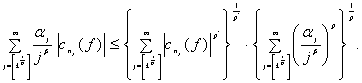
Тогда из (5) будем иметь

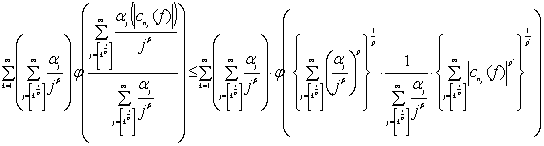(6)

В условии (4) полагая , и применяя неравенство (4) из (6) получим

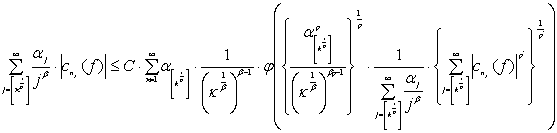(7)

По условию теоремы возрастающая последовательность, поэтому

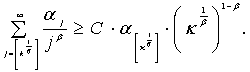(8)

Из неравенства (7) и (8) получим

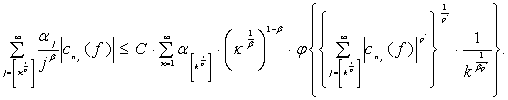
Воспользовавшись неравенством Хаусдорфа-Юнга ([1]) и леммой 1 имеем

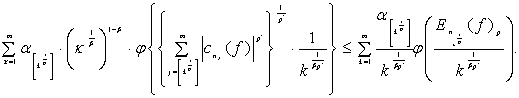(9)

Из неравенства (5) и (9) получим:

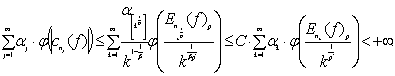
Следовательно,

Теорема доказана.

Литературы:

1. Бари Н.К., Тригонометрические ряды, М., Физматгиз, 1961.

2. Ogata N., On the absolute convergence of lacunary Fourier series.// Math.Japanica. – 1999. - vol 49. - No. 2. - р. 241-245.

3. Стечкин С.Б., Об абсолютной сходимости ортогональных рядов. I// Математический сборник. - 1951. - т. 29. - №1.- С. 225-232.

4. Чан Минь., Абсолютная сходимость рядов из коэффициентов Фурье по ортонормированной системе//Вестн. Моск. ун-та. Сер.1. Математика. Механика. - 1992. - №2. - С. 37-42.

5. Patadia J.R., Shah V.M., On the absolute convergence of lacunary Fourier series. // J.Indian Math.Soc. - 1980. – 44. - р. 267-273

6. Leindler L., Comments on the absolute convergence of Fourier series.//Hokkaido Math.J. - 2001. - р.221-230.