Математика/ 1. Дифференциальные и интегральные уравнения

К.ф.-м.н. Есмаханова К.Р.,  ст. преп. кафедры ВМиММ  Ильясова М.Т.,  МНС Мырзакулова Ж.Р., ст. преп. кафедры ВМиММ  Тунгушбаева Д.И.

Евразийский национальный университет им.Л.Н.Гумилев

Темная энергия в некоторых интегрируемых ФРУ космологических моделей

Недавние измерения красного смещения и соотношений свечение - расстояние суперновых типа  указывают на то, что расширение Вселенной ускоряется [1, 2]. Это оказывается в строгом несогласии со стандартной картиной материи доминирующей во вселенной. Эти наблюдения могут сопровождаться теоретически постулированием того, что определенная экзотическая материя (темная энергия) с отрицательным давлением доминирует в настоящее эпохе нашей вселенной. Понимание природы темной энергии и многих связанных с ней задач является одной из обширных проблем в современной космологии ( например, см. [8-10]). Почти все модели темной энергии работают в пространстве-времени ФРУ, то есть, другими словами, являются моделями ФРУ. Практически, все космологические модели ФРУ для темной энергии сталкиваются с некоторыми трудностями, связанными с некоторыми нетривиальными проблемами как проблема совпадения, проблема fine-turn и т.д. Такие и другие проблемы космологии требуют более внимательного исследования физической и математической природы моделей ФРУ. В этом контексте важно для изучения интегрируемых (и неинтегрируемых) случаи моделей ФРУ. Здесь мы упомянем хорошо известный факт, что Эйнштейна гравитационные уравнения и их некоторые обобщения признать, интегрируемые редукции [3-4]. В настоящей работе мы рассматриваем некоторые космологические модели вызванные некоторыми известными линейными и нелинейными обыкновенными дифференциальными уравнениями (ОДУ) второго порядка [5-6].

В этом раздел организована следующим образом. В части 2 даем некоторую основную информацию по космологическим моделям ФРУ для случая плоского пространства-времени. В следующей части мы изучаем некоторые неинтегрируемые космологические модели ФРУ. В части 4 был рассмотрен новый класс интегрируемых моделей ФРУ. Эти результаты были обобщены для модифицированных  и  гравитационных моделей в части 5 и 6. Части 7 и 8 посвящены описанию скалярного поля и двумерному обобщению некоторых моделей. В последней части мы даем заключение.

 

           Космология ФРУ. Начинаем со стандартного гравитационного действия

                                                  (1)

Здесь  - скалярная кривизна и  - лагранжиан материи. Теперь мы рассматриваем пространство-время ФРУ с масштабным фактором  и метрикой

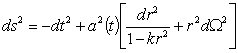                                        (2)

Здесь  может принимать любое значение, но это относится к (−, 0, +) кривизнам согласно сигнатуре. Положим  посчитаем символ Кристоффеля следующим образом:

 

     

                      (3)

       

Они приводят к

 

                        (4)

со скаляром Риччи

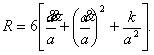                                                                        (5)

Уравнения Фридмана записываются как

                                                 (6)

где что  подразумевает отталкивательную гравитацию. Используя параметр Хаббла, эти уравнения могут быть записаны следующим образом:  

                                        (7)

Уравнениями Фридмана с космологической константой для однородной изотропной модели Вселенной являются следующие:

                                   (8)

В настоящей работе мы рассматриваем случай:  и полагаем . Если пространство-время ФРУ заполнено жидкостью плотности энергии  и давления, тогда сохранение тензора энергии-импульса

                                                                                        (9)

приводит к

                                                                         (10)

где точка представляет дифференцирование по . Так уравнения для действия (2.1) мы можем переписать в - форме

                                                                            (11)

                                                                                           (12)

                                                                           (13)

или в  - форме

                                                                            (14)

                                                                                           (15)

                                                                            (16)

где

В настоящей работе мы изучаем некоторые космологические модели, например, с уравнение состояния (УС)  (смотри, [7-10])

                                 (17)

где  и  - некоторые функции от и .

          В этом работе  рассмотрели уравнения Эйнштейна. Связь между нелинейными уравнениями Шредингера и Эйнштейна доказано другими авторами [6-10]. Уравнения Эйнштейна являются основными уравнениями космологии.

Таким образом во втором разделе рассмотрены уравнения Эйнштейна и некоторые космологические модели ФРУ с параметрическим УС, где e-фолдинг  играет роль параметра. Для построения космологической модели в явном виде  требуем, чтобы   являлось решением некоторых линейных и нелинейных ОДУ второго порядка. Если такие ОДУ интегрируемы, тогда соответствующие модели ФРУ также интегрируемы. Это значит, что такие модели допускают все характеристики интегрируемых систем такие как  - солитонные решения, коммутирующие интегралы, представления Лакса и т.д.

 

 

Список литературы

 

1.                                                                                                                     Perlmutter S. et al. Astrophys. J.  517, 565-586 (1999)

2.                                                                                                                     Riess et al. Astron. J.  116, 1009-1038 (1998)

3.                                                                                                                     Nojiri S., Odintsov S.D., Tsujikawa S. Phys. Rev. D,  71, 063004 (2005)

4.                                                                                                                     Nojiri S., Odintsov S.D. Phys. Rev. D,  72, 023003 (2005)

5.                                                                                                                     Nojiri S., Odintsov S.D. Is the future universe singular: dark matter versus modified gravity?, [arXiv:0911.2781]

6.                                                                                                                     Lopez-Revelles A.J., Elizalde E. Universal procedure to cure future singularities of dark energy models, arXiv:1104.1123

7.                                                                                                                     Tsyba P.Y., Kulnazarov I.I., Yerzhanov K.K., Myrzakulov R. International Journal of Theoretical Physics,  50, 1876-1886 (2011)

8.                                                                                                                     Myrzakulov R. Fermionic K-essence, [arXiv:1011.4337]

9.                                                                                                                     Jamil M., Myrzakulov Y., Razina O., Myrzakulov R. Modified Chaplygin Gas and Solvable F-essence Cosmologies, [arXiv:1107.1008]

10.                                                                                                                 Kulnazarov I., Yerzhanov K., Razina O., Myrzakul Sh., Tsyba P., Myrzakulov R. Eur. Phys. J. C,  71, 1698 (2011), [arXiv:1012.4669]