К.ф.м.н. Корольов М.Є., студ. Кірноз І.А.

Автомобільно-дорожній інститут ДНВЗ

«Донецький національний технічний університет»

Використання КЛАСИЧНИХ МЕРЕЖНИХ АЛГОРИТМІВ оптимізації В транспортІ

В цілому алгоритм побудови мінімального остового дерева не характеризується значною трудомісткістю, а тому знайшов широке використання серед проектування доріг, трубопроводів, кабельної мережі та ін. Метою такого проекту є створення такої мережі, де б мінімізувалася довжина шляхів, а тому такий проект в цілому був би і економічним, і ефективним.

Не є виключенням використання в даній задачі алгоритму побудови мінімального остового дерева. Тож використаємо цю модель відносно проекту розвитку західного регіону Криму.

Рада міністрів Криму постановила задачу про розробку проекту розвитку західного регіону півострова. Одним із підрозділів цього проекту є побудова мережі доріг з твердим покриттям, що з’єднують населені пункти Знаменське, Окунівка, Мар’їно, Красносельське, Оленівка з містом Чорноморське (рис.1). Необхідно спланувати найбільш економічну дорожню мережу.

Для рішення даної задачі необхідно в першу чергу розглянути алгоритм побудови мінімального остового дерева, що припускає з’єднання усіх вузлів мережі за допомогою шляхів найменшої довжини.

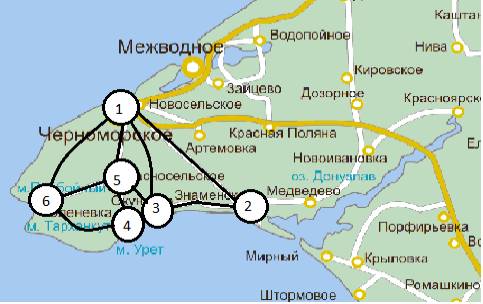
Рисунок 1 – Існуюча дорожня мережа на західному регіоні Криму

Умовні позначення: 1 – Чорноморське; 2 – Знаменське; 3 – Окунівка;

4 – Мар’їно; 5 – Красносельське; 6 – Оленівка.

Послідовні ітерації виконання алгоритму представлені на рис.2. Тут тонкими лініями показані ребра , що з'єднують вузли , які належать множинам C_k і , серед яких шукається ребро з мінімальною довжиною. Знайдене ребро показане пунктирною лінією. Товстими суцільними лініями позначені ребра з'єднуючі вузли множини C_k (і які раніше позначалися пунктирними лініями) та вузли, що входять до множини C_k. Вузли, що входять до нанесені тонкими суцільними лініями.

Рішення у виді мінімального остового дерева отримано на 5-й ітерації (рис.2 ). Сума ребер на отриманому мінімальному остовому дереві дорівнює:

9 + 11 + 8 + 5 + 16 = 49 км.

Тож сумарна мінімальна відстань, що з’єднує населені пункти Знаменське, Окунівка, Мар’їно, Красносельське, Оленівка з містом Чорноморське складає 49 км.

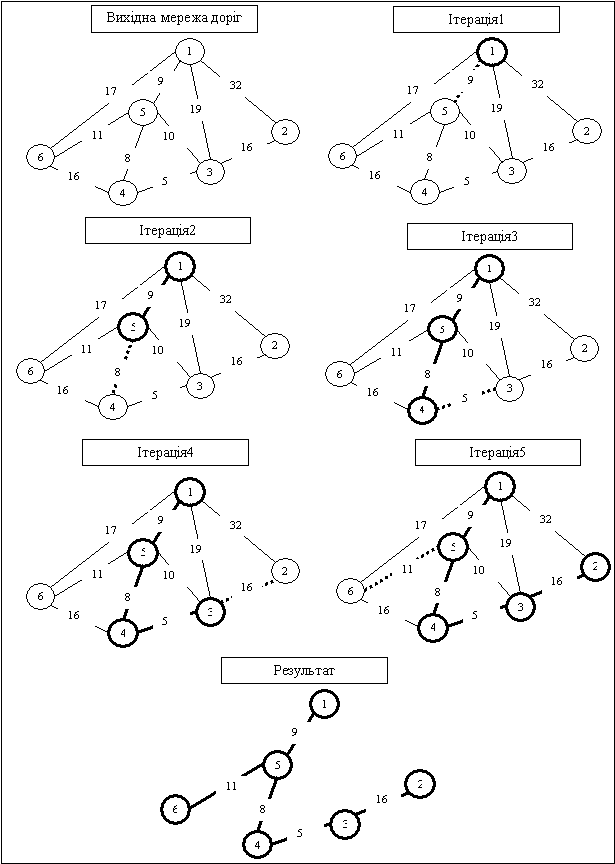
Рисунок 2 – Послідовні ітерації виконання алгоритму

Література:

1. Шикин Е.В., Шикина Г.Є. Исследование операций. – М: ТК Велби,

Изд-во Проспект, 2006 – с. 21-28, 34-42.

2. Катренко А.В. Дослідження операцій: Підручник. Видання третє, виправлене і доповнене. – Львів: «Магнолія» , 2009 – с118-122.

3. Кутковецький В.Я. Дослідження операцій: навчальний посібник. К: Вид-во ТОВ "Видавничий дім "Професіонал", 2004 – с.197-199.

4. Зайченко Ю.П. Исследование операций. Учебник. - 6 изд., перераб. и доп. К: Издательский Дом "Слово", 2003. – с.312-319.

5. Вентцель. Исследование операций. Задачи, принципы, методология. Учебное пособие для ВУЗов. М.: Высш. шк., 2001. – с.29-31.

6. Карагодова О.О. Кігель В.Р., Рожок В.Д. Дослідження операцій: навчальний посібник. – К: Центр учбової літератури, 2007 – с.98-106.

7. Волков И.К., Загоруйко. Исследование операций. М.: Изд-во МГТУ им. Н.Э.Баумана, 2002 – с. 172-180.