К.ф.м.н. Корольов Є.О., студ. Кірноз Н.А.

Автомобільно-дорожній інститут ДНВЗ

«Донецький національний технічний університет»

ПРАКТИЧНЕ Використання АЛГОРИТМУ «МАКСИМАЛЬНИЙ ПОТІК»

Ідея даного алгоритму полягає в знаходженні наскрізних шляхів з позитивними потоками від джерела до стоку. Актуальність завдання про максимальний потік постійно зростає в місці з будівництвом трубопроводів, нових доріг, росту користувачів Інтернету й будь-яких інших мереж.

Не є виключенням використання в даній задачі алгоритму про максимальний потік. Тож використаємо цю модель відносно проекту пересування вболівальників у місті.

В місто Донецьк, на залізничний вокзал (початковий пункт) для перегляду одного з матчів «EURO 2012», який повинен пройти на стадіоні «Донбас-Арена» (стік) прибули 6000 вболівальників. Спочатку вболівальники відправились у наступні міста відпочинку: готель «Великобританія», мотель та торгівельно - розважальний комплекс «Донецьк - Сіті». Для того щоб потрапити в указані місця, вболівальники використали міський пасажирський автотранспорт, зокрема маршрутами : 2, 38-Б, 83, 46-Б, 32, 37, 38, 36. Визначити максимальний потік від початкового до кінцевого пункту, дати оцінку ступеню використання маршруту. Нижче приведено номера маршрутів, які обслуговують наступні пункти : маршрут №37 пункт 1-2, №32-1-3; №2-1-4; №38-2-5, №36-2-3; №46-Б-3-4, №83-3-5, №38-Б- 4-5.

Для рішення даної задачі необхідно в першу чергу виділити на карті пересування вболівальників у місті Донецьк. Отримаємо певну модель (рис.1). З’єднаємо всі пункти прямими лініями.

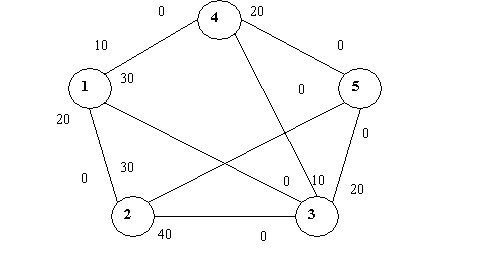
Рисунок 1 – Модель пересування вболівальників у місті

Умовні позначення: залізничний вокзал-1, готель «Великобританія» - 2, мотель - 3, торгівельно – розважальний комплекс «Донецьк - Сіті» - 4, «Донбас - Арена» - 5.

Таблиця 1 – Результати обчислень пропускних здатностей.

Ребро	( )-(cij, сji)	Величина потоку	Напрямок
(1,2)	(20, 0) - (0, 20) = (20. -20)	20	12
(1,3)	(30, 0) - (0, 30) = (30, -30)	30	1 3
(1,4)	(10, 0)-(0, 10) = (10,-10)	10	14
(2,3)	(40,0)-(40,0) = (0,0)	0	-
(2,5)	(30,0)-(10, 20) = (20,-20)	20	2 5
(3,4)	(10, 5)-(0, 15) = (10,-10)	10	3 4
(3,5)	(20,0)-(0,20) = (20,-20)	20	35
(4,5)	(20, 0) - (0, 20) = (20, -20)	20	4 5

Реалізувавши розроблену модель (рис.2) можна зробити висновок, що максимальна величина потоку (3000 вболівальників) буде між напрямком 1-3,тобто між залізничним вокзалом та мотелем. Тому треба уділити увагу маршруту 32, який перевозить пасажирів між пунктами 1-3. Прийняти ряд рішень по збільшенню кількості автобусів на час проведення Euro 2012. Маршрут 36, якій перевозить пасажирів між пунктами 2-3(між готелем «Великобританія» та мотелем),буде не актуальним (не раціональним, тому що величина цього потоку дорівнює 0) . Всі останні маршрути мають майже однакові величини, тому будуть користуватися майже однаковим попитом серед вболівальників.

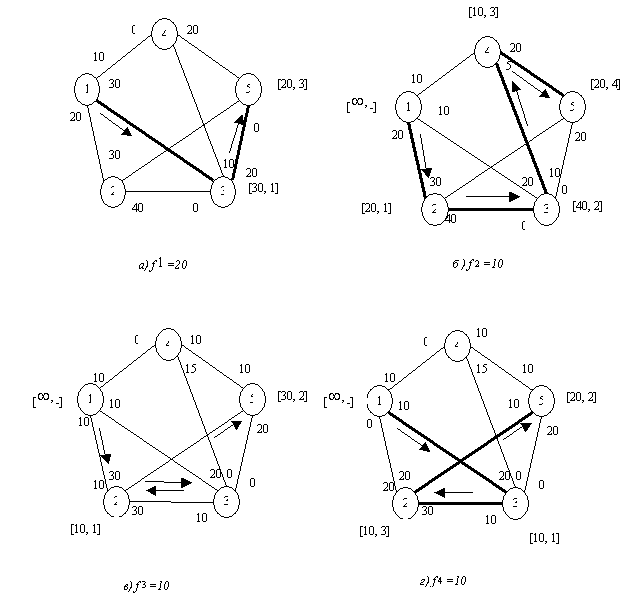
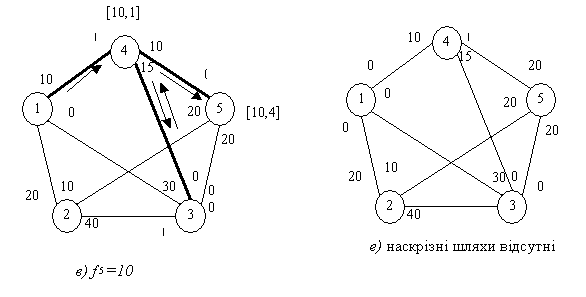
Рисунок 2 – Послідовні етапи реалізації завдання

Література:

1. Берж К. Теория графов и ее применения. М.: Иностранная литература, 1962. - 319с.

2. Вагнер Г. Основы исследования операций. - М., Мир, 1972. -336 с.

3. Деордица Ю.С. Исследование операций в планировании и управлении: Учебное пособие / Ю.С. Деордица, Ю.М. Нефедов . – 1991 .212с.

4. Исследование операций: В 2-x томах. Под ред.ред. Дж. Моудера, С. Элмаrраби.- М., Мир, , 1981.Т-1 - 712 с., ил.

5. Йенсен П., Барнес Д :Потоковое программирование. Пер. с англ.1984. 392 с.

6. Костевич Л. С. Математическое программирование: Информ. технологии оптимальных решений: Учеб. пособие / Л.С. Костевич. — Мн.: Новое знание, 2003. — 424 с.

7. Форд Л., Фалькерсон Д.: Потоки в сетях. Пер. с англ. — М. : Издательство «МИР»,1966. — 276 стр.